一、策略迭代
一旦使用vπ改善了策略π，产生了更好的策略π0，我们就可以计算vπ0并再次对其进行改进，产生更好的π00。因此，我们可以获得一系列单调改善的策略和值函数：
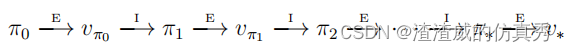
其中E−→表示策略评估，I−→表示策略改进。每个策略都保证比前一个策略有严格改进（除非它已经是最佳的）。因为有限MDP只有有限数量的策略，所以这个过程必须在有限次迭代中收敛到最优策略和最优值函数。
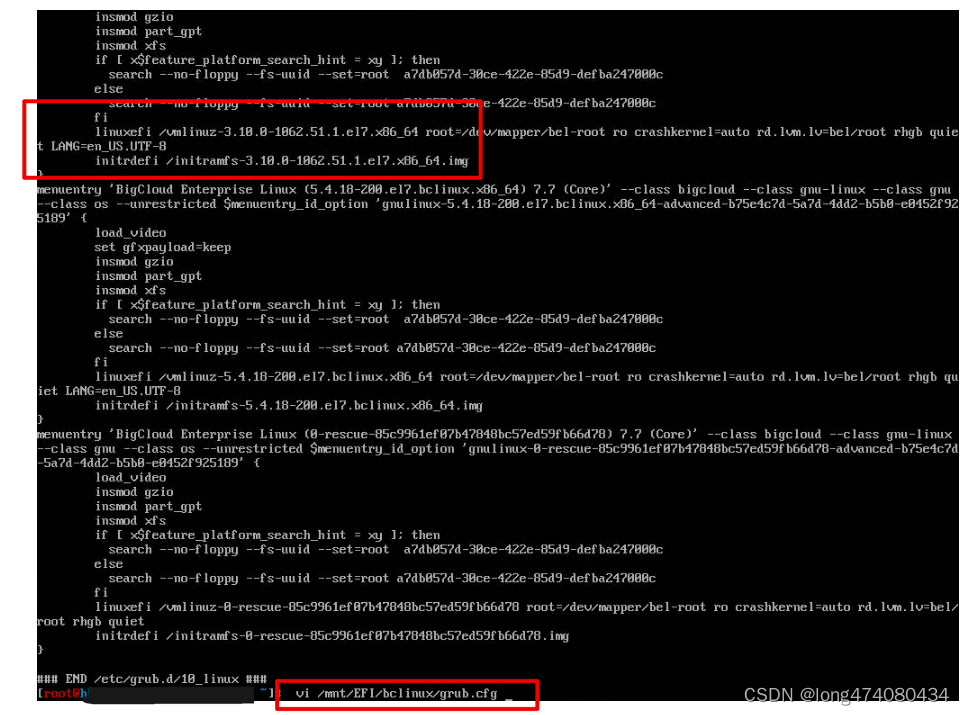
这种方法称为策略迭代。完整的算法如图1所示。请注意，每次策略评估本身都是迭代计算，都是从上一个策略的值函数开始的。这通常会导致策略评估的收敛速度大大提高（可能是因为值函数从一个策略到下一个策略变化不大）。
这种寻找最优策略的方法称为策略迭代。完整的算法如图1所示。请注意，每次策略评估本身都是迭代计算，都是从上一个策略的值函数开始的。这通常会导致策略评估的收敛速度大大提高（可能是因为值函数从一个策略到下一个策略变化不大）。
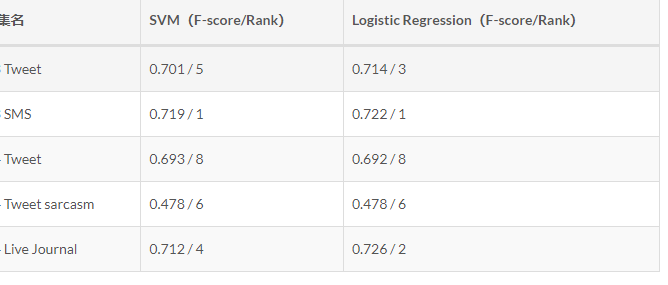
策略迭代通常在出人意料的少量迭代后就能收敛。网格世界的示例说明了这一点。底部左边的图显示了等概率随机策略的值函数，底部右边的图显示了针对该值函数的贪婪策略。策略改进理论保证了我们这些策略优于原始的随机策略。然而，在这种情况下，这些策略不仅是更好的，而且是最佳的，以最少的步骤到达终止状态。在这个例子中，策略迭代只需一次迭代就能找到最优策略。
图1
图1中，针对v∗的政策迭代（使用迭代策略评估）算法存在一个不易察觉的错误，即如果策略在两个或更多个同样好的策略之间持续切换，该算法可能永远无法终止。可以通过添加额外的标志来修复此错误，但这会使伪代码变得非常难看。
二、典型示例
Jack经营着一家全国范围的汽车租赁公司的两个门店。每天，每个门店都会有一定数量的顾客前来租车。如果Jack手头有可用的汽车，他会将车出租出去，并获得该全国性公司提供的10美元信用。如果他在该门店没有汽车可用，那么这笔生意就泡汤了。汽车在归还后的第二天就可以出租。为了确保汽车在需要的地方可用，Jack可以在一晚之间将汽车从这两个地点之间进行调换，每次移动的费用为2美元。我们假设每个地点请求和归还的汽车数量是泊松随机变量，这意味着其概率是
，其中λ是期望值。假设第一个和第二个门店的请求期望值λ分别为3和4，归还期望值分别为3和2。为了简化问题，我们假设每个地点最多只能停放20辆汽车（超出数量的汽车将被退还给全国性公司，从而从问题中消失），并且每晚最多可以从一个地点移动5辆汽车到另一个地点。我们将贴现率γ设置为0.9，并将此问题表述为一个持续的有限MDP，其中时间步长为天，状态为每天结束时每个地点的汽车数量，行动是在一夜之间两个地点之间移动的汽车数量的净差额。图2显示了从永不移动任何汽车的策略开始的政策迭代找到的策略序列。
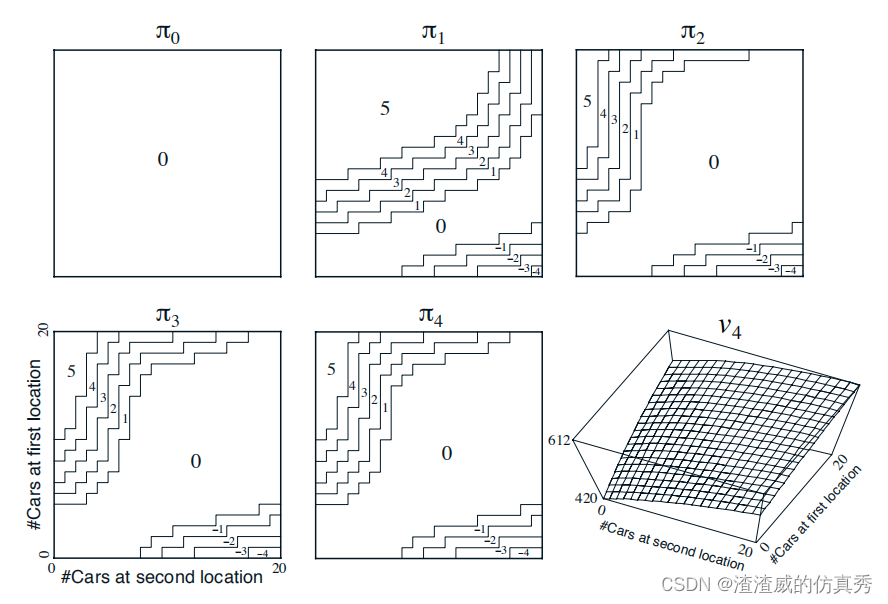
图2
图2显示了政策迭代在Jack的汽车租赁问题上找到的政策序列，以及最终的状态值函数。前五幅图展示了每天结束时每个地点的汽车数量，从第一个地点到第二个地点的汽车数量（负数表示从第二个地点转移到第一个地点的汽车数量）。每个连续的政策都是对前一个政策的严格改进，最后一个政策是最佳的。
