目录
前言
一、梯度下降相关数学概念
二、最速下降法实战
2.1、例图1
2.2、Matlab代码实现
2.3、例题2
三、小结
前言
最速下降法,在SLAM中,作为一种很重要求解位姿最优值的方法,缺点很明显:迭代次数太多,尽管Newton法(保留目标函数的二阶项Hessian矩阵)改善了“迭代次数过多”这一缺点,但是Hessian矩阵规模庞大(参考:特征匹配点成百对),计算较为困难。Gaussian-Newton法在Newton原有基础上,用的是一阶雅克比的转置*一阶雅克比 JTJ 来近似 Hessian, 但是,这里的近似替换 JTJ并不一定正定。一般,主流非线性优化方法:Levenberg-Marquadt、Dog-leg较为常用,这里不作介绍。
在深度学习中是一样的道理,模型训练参数可能有几百万到几千万,每次训练前向传播要计算loss,一阶偏导数,然后依据最速下降法更新梯度。
一、梯度下降相关数学概念

个人理解:
![]()
是方向偏导数,我们不仅要使得梯度下降,还要以最快的步伐下降。


x* 是无约束问题的局部最优解 =》 x*是其目标函数的驻点
(回想起SVM当中求解有约束目标函数最优值,利用拉格朗日乘子法进行转换。)
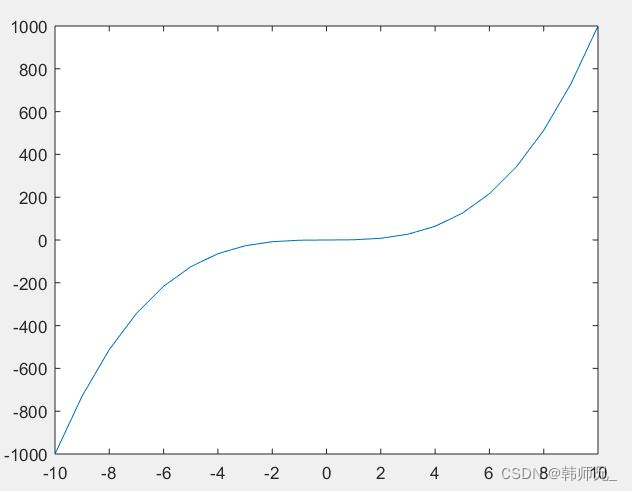
例如:在 y = x^3的曲线当中,x = 0处是 极大值点,也不是极小值点,称作:鞍点。

理解定理3:我们翻开书,看到如下概念:
性质
(1)如果一个函数f(x)在某个区间I上有f''(x)(即二阶导数)>0恒成立,那么对于区间I上的任意x,y,总有:
f(x)+f(y)≥2f[(x+y)/2],如果总有f''(x)<0成立,那么上式的不等号反向。
几何的直观解释:如果一个函数f(x)在某个区间I上有f''(x)(即二阶导数)>0恒成立,那么在区间I上f(x)的图象上的任意两点连出的一条线段,这两点之间的函数图象都在该线段的下方,反之在该线段的上方。
(2)判断函数极大值以及极小值。
结合一阶、二阶导数可以求函数的极值。当一阶导数等于0,而二阶导数大于0时,为极小值点。当一阶导数等于0,而二阶导数小于0时,为极大值点;当一阶导数和二阶导数都等于0时,为驻点。
(3)函数凹凸性。
设f(x)在[a,b]上连续,在(a,b)内具有一阶和二阶导数,那么,
(1)若在(a,b)内f''(x)>0,则f(x)在[a,b]上的图形是凹的;
(2)若在(a,b)内f’‘(x)<0,则f(x)在[a,b]上的图形是凸的。
![]()

二、最速下降法实战
2.1、例图1
来做一道数学题,如能理解,便能深刻理解算法。

2.2、Matlab代码实现
准备相关脚本函数(Matlab脚本):
function [ y ] = GDMin2(fx,var,x,e,MAX)
% 最速梯度下降法求解函数极小点
% 参数描述------------------------------
% fx 符号表达式 如fx = (x1-2)^4+(x1-2*x2)^2;
% var 符号变量列表 如:syms x1 x2;var= [x1;x2];
% x 起始位置
% e 精度控制
% MAX 最大迭代次数控制
% ------------------------------if nargin < 5MAX = 10;%设置默认最大迭代次数
end
precision = 3;%显示精度控制%开始循环迭代
%direction存贮搜索方向
%step 存贮步长bfound = 0;
for k=1:1:MAXdirection = getNextDirecrion(fx,var,x);disp('------------------------------');fprintf('d[%d]=:',k);disp( vpa(direction',precision) );if normest(direction) <= ey = x;bfound = 1;%得到结果时置为1break;elsestep = getNextStep(fx,var, x,direction);%计算步长if isempty(step)error('can not find a proper step.');end%打印求解过程fprintf('X[%d]=:',k);disp( vpa(x',precision) );fprintf('step(%d)=: ', k);disp( vpa(step,precision) );disp('------------------------------');x = x+step*direction;%计算下一个位置end
end
if bfound == 1disp('min value of:');disp( vpa( subs(fx,var,y),precision) );
end
end%根据位置xk,获取搜索方向
function [direction] = getNextDirecrion(fx,var,xk)gx = gradient(fx,var); %计算梯度函数direction = -subs(gx,var,xk);%计算搜索方向
end%根据位置xk和方向dk,获取搜索步长step
%注意符号表达式求导数的根时返回值转换为double类型
function [step] =getNextStep(fx,var,xk,dk)syms lambda;phix = subs(fx,var,xk+lambda*dk);phix_diff = diff(phix);step = double(solve(phix_diff,'Real',true));%求取导函数的实数根
end在MATLAB命令行键入:
clear all;
syms x1 x2;
X = [x1;x2];
fx = x1 - x2 + 2*x1^2 + 2*x1*x2 + x2^2;
x1 = [0;0];
e = 0.3;
minVal = GDMin2(fx,X,x1,e)结果打印如下:
结果:------------------------------
d[1]=:[ -1.0, 1.0]X[1]=:[ 0, 0]step(1)=: 1.0------------------------------
------------------------------
d[2]=:[ 1.0, 1.0]X[2]=:[ -1.0, 1.0]step(2)=: 0.2------------------------------
------------------------------
d[3]=:[ -0.2, 0.2]min value of:
-1.2minVal =-4/5
6/5和手动结算的结果是一样的在 x 取值 [-0.8, 1.2]的时候,取得满足精度的值。
2.3、例题2
这里再看一道简单的数学题,当梯度下降起始点x取值为3和2的时候,收敛步数是不一样的。

我们看前两步;画出其迭代路线:
clear all;
clc;
close all;
x = 0:0.1:8
fx = (x(1,:) - 4).^2plot(x, fx);
hold on%% 标出点
plot(3, 1, '-ro');
plot(4, 0, '-ro');
hold on%% 连线
%% plot([x1,x2...], [y1,y2,...])
plot([3 4],[1 0], '-g');
hold off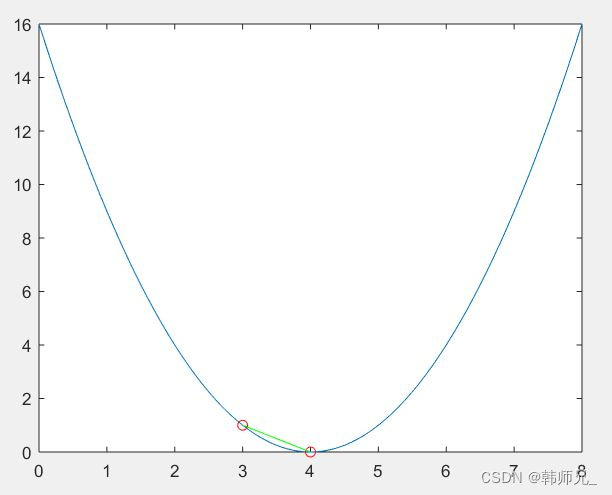
两步就收敛;现在,如果我们将初始值(startpoints)改为:x = 2;再根据上述求解过程,画出迭代路线:
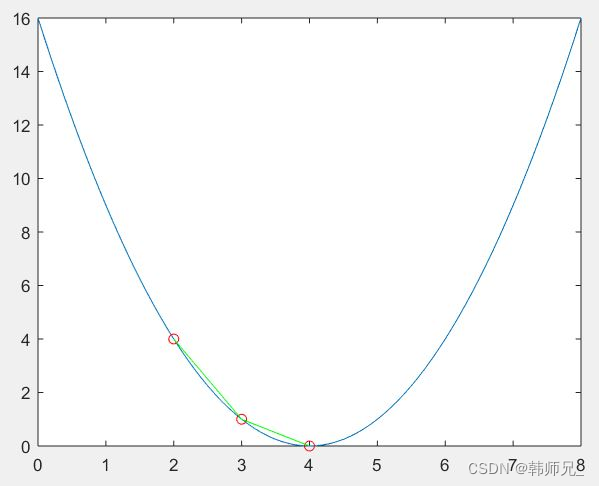
可以看到,起始点是 x = 2 比 x = 3的迭代次数多一次,所以选取一个好的初始值十分重要;同样,
三、小结
- 在SLAM当中,例如:3D-3D映射;我们在RANSAC框架下,基于PNP/ICP 计算出位姿初始值,这样一个初始值,在后续BA当中,是一个较为理想的初始值。
- 在深度学习中,预训练模型能够加速收敛。