讲解关于slam一系列文章汇总链接:史上最全slam从零开始，针对于本栏目讲解的 卡尔曼家族从零解剖 链接 :卡尔曼家族从零解剖-(00)目录最新无死角讲解：https://blog.csdn.net/weixin_43013761/article/details/133846882
 
$文末正下方中心提供了本人联系方式，点击本人照片即可显示WX\to 官方认证$
 

一、前言

上一篇博客，讲解的内容确实太多了，推导过程比较复杂，为了有一个整体的认知，方便后续学习，所以这里再花费一个篇幅梳理一下知识点。首先有最基本的贝叶斯公式：
$$f_{X\mid Y}(x\mid y)=\frac{f_{X,Y}(x,y)}{f_Y(y)}=\frac{f_{Y\mid X}(y\mid x)f_X(x)}{{\int }_{-\infty }^{+\infty }{f}_{Y\mid X}(y\mid x)f_X(x)\mathrm{d}x}=\eta f_{Y\mid X}(y\mid x)f_X(x)\text{\hspace{1em}(01)}$$ 有了这个贝叶斯公式呢，接着做了两个重要的假设：

        $(01):$ $X_0$ 与 $Q_1$、$Q_2$、$Q_3$、$......$、$Q_k$ 相互独立。
        $(02):$ $X_1$ 与 $R_1$、$R_2$、$R_3$、$......$、$R_k$ 相互独立。

基于上上述的假设，我们假设了随机变量的状态方程与观测方程：
$$\begin{gathered} X_k=f(X_{k-1})+Q_k \\ {Y}_k=h(X_k)+R_k\text{\hspace{1em}(02)} \end{gathered}$$然后我们进行随机变量的递归过程，图示如下(上一篇博客图二简化精华版)：

上图为大致递推流程，但是这个流程是很难走下去的，为什么呢？假设现在初始状态 $X_0$、$f(x)$状态转移方程、$h(x)$ 测量方程、 与初始状态转移噪声 $Q_1$ 与 测量噪声 $R_1$、以及各个时刻的观测随机变量 $Y_1$到 $Y_k$，但是我们依旧没有办法递推出 $X_k^{+}$，因为我们不知道 $Q_2$ 到 $Q_k$，$R_2$ 到 $R_k$，注意，这里是说随机变量 $Q_k$ 与 $R_k$ 的具体取值不知道是多少，而不是说关于他们的函数表达式不知道(后续学习卡尔曼滤波会有更加深的体会)，所以根据状态方程与测量方程进行了如下推导：

$(01):$ 根据状态方程推导出先验概率密度函数 $f_{X_k}^{-}(x)$，其等价于(01)式中的 $f_X(x)$。
$$f_{X_k}^{-}(x)=\frac{\mathrm{d}{F}_{X_1}^{-}(x)}{\mathrm{d}x}={\int }_{-\infty }^{+\infty }{f}_{Q_k}[x-f(v)]f_{X_{k-1}}^{+}(v)\mathrm{d}v\text{\hspace{1em}(03)}$$

$(02):$ 根据测量方程推导出出似然概率密度函数 $f_{Y_k\mid X_k}(y_k\mid x)$，等价于(01)式中的 $f_{Y\mid X}(y\mid x)f_X(x)$。$$f_{Y_k\mid X_k}(y_k\mid x)=f_{R_k}\left[y_k-h(x)\right]\text{\hspace{1em}(04)}$$
$(03):$ 最后参照(01)式子，可得后验概率密度函数 $f_{X_k}^{+}(x)$：
$$f_{X_k}^{+}(x)={\eta }_k\cdot f_{X_k|Y_k}(x)\cdot f_{X_k}^{-}(x)={\eta }_k\cdot f_{R_k}\left[y_k-h(x)\right]\cdot {\int }_{-\infty }^{+\infty }{f}_{Q_k}[x-f(v)]f_{X_{k-1}}^{+}(v)\mathrm{d}v\text{\hspace{1em}(05)}$$$${\eta }_k=[{\int }_{-\infty }^{+\infty }(f_{R_k}\left[y_k-h(x)\right]\cdot {\int }_{-\infty }^{+\infty }{f}_{Q_k}[x-f(v)]f_{X_{k-1}}^{+}(v)\mathrm{d}v\mathrm{d}x{]}^{-1})\mathrm{d}x\text{\hspace{1em}(06)}$$
需要注意，其上的 $f_{Q_k}$ 与 $f_{R_k}$ 都为概率密度函数(PDF)。求得 后验概率密度，对齐进行积分即可得到概率分布，进一步求期望即可。

二、技术难点

公式确实推导出来了，但是很明显上式是一个广义结果，并没有实例化，比如 $f(x)$，$h(x)$。如果这两个是函数十分复杂，比如非线性。那么上式则设计到两个非线性无穷积分的运算，也就是 (03) 式与 (06) 式。亦或者 $f_{Q_k}(x)$ 与 $f_{R_k}(x)$ 十分复杂，同样会导致非线性无穷积分的运算，这样有可能会导致无法求解。当然，这个推导出来的结果就没有任何作用了。

所以呢，在实际的应用中，基于贝叶斯的不通算法会有不同假设，比如令 $f(x)$，$h(x)$ 为线性函数，那么显然，其就应用场景就存在局限性了，卡尔曼滤波就是一种具体化的实现。另外还有扩展卡尔曼滤波，其能够处理一些非线性的复杂场景，后续也会为大家详细分析。依照不通实现方式，对基于贝叶斯滤波思想的方法进行了归类如下：

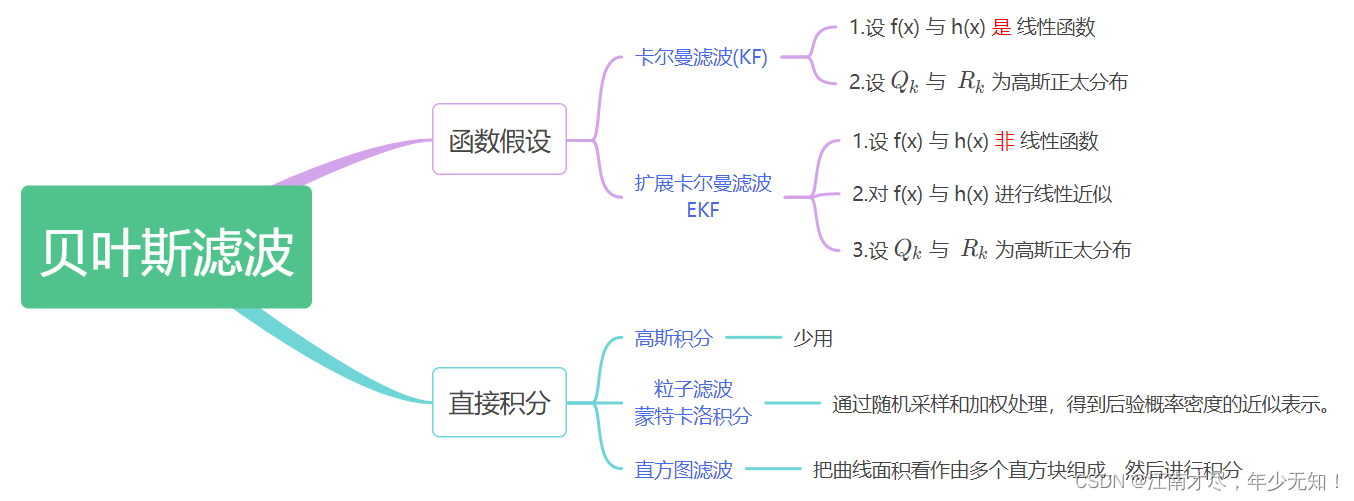
上图后续会继续扩充，暂时只做简要介绍。需要注意的是，无论是卡尔曼滤波、例子滤波、直方图滤波、他们都是属于部分实例化，而非完全实例化。这里回顾一下前面的说辞：

$核心(个人理解)：$ 首先贝叶斯滤波其并不是具体某一种算法的具体实现，而是一种思想指导，就类似于 C++ 编程中的抽象类，定义了一些虚函数而已。这里举一个恰当一些的例子，比如说小学语文课，小朋友会学习笔画，一横、一竖、一撇等等。这些就类似于贝叶斯滤波，是比较基础比较抽象的，但是通过笔画的组合，可以实现各种中文子图，如你、我、他、好、坏等等，这些实际的字就好像是卡尔曼滤波、粒子滤波等等。虽然每个小朋友写的字，只要写(笔画组合)正确了，那么就是一个正确的字，但是呢？每个小朋友写的字迹都是不一样的，有的好看，有的不好看，有的大，有的小，但是这些字都是属于小朋友自己的特色。这里就好比，各行各业，各个不同的算法，他们或许都会使用到卡尔曼滤波，但是却不尽相同，多少会存在一些区别。所以我们在使用这些实例化的算法，也需要根据实际情况做一些改动或调整。

再者，根据状态方程与观测方程是否非线性，分为线性(L)系统或非线性(NL)系统，根据随机变量是否符合正太分布分为高斯(G)系统，与非高斯(NG)系统，当然他们是可以混合的，比如 LG(线性高斯) 系统就是最简单的一类，NLNG(非详细非高斯) 系统则是最为复杂的一类。通常来说最参见的系统是 NLG(非线性高斯) 系统。

三、额外提及

在前面推导过程中，都是基于一维进行推导的，如随机变量 $X_k$、$Y_k$、$Q_k$、$R_k$、$\cdots$ 代表的都是一个数值，但是我们在实际应用时，基本都是二维以上的，如本人在 slam 中遇到的基本都是三维的变量，很少说存在一维的，虽然也可以通过一维的方式解决，但是这样显得太 low ，代码的可读性会极度下降。

就拿状态变量 $X_k$ 来说，其通常都是 3 维以上的，甚至更多，比如机器人的状态，对于 slam 来说其至少要包含 旋转与平移，也就是 $R$、$\mathbf{p}$。旋转矩阵 $R$ 可以用多种形式表示，
如使用四元素来表示旋转，那么共 7=4+3 个状态量，如果使用李代数来表示旋转，则共 6=3+3 个状态量。可以知道的是，根据状态方程 $X_k=f(X_{k-1})+Q_k$ 可知，若 X_k 的维度为 n，那么噪声分布通常维度也为 n，因为这样才能完成加法运算。也比较好理解，噪声就是状态量的抖动与不确定性。

根据前面的推导，可以知道贝叶斯滤波底层原来是一种递归的方式，其本质基于前一个状态的概率分布对下一个状态的概率分布进行预测，这种方式的计算量比较少，通常都能够实时，特别适合 slam 中在线位姿估算。

除了基于贝叶斯滤波这种递推的方式，还有一种批量优化(MAP)的方式，这里先考虑一极端的方式，及考虑到 $0\sim k$ 时刻的所有数据，同时对 $0\sim k$ 时刻的所有状态变量 $x=x_{0:k}=(x_0,\cdots ,x_k)$ 进行优化，首先这里都使用小写，代表随机过程的具体化，另外这里 $x$ 是一个宏观概念，其没有下标，即代表多个变量。在数学中经常使用 $\check{x}$ 表示先验，$\hat{x}$ 表示后验，帽子分别向下与向上(有兴趣的朋友可以去阅读一下机器人学中的状态估计)。除基本状态量外，还有一些额外(控制)量 $v=(\check{x_0},v_{1:k})=(\check{x_0},v_1,\cdots ,v_k)$，以及 $0\sim k$ 时刻的观测 $y=y_{0:k}=(y_0,\cdots ,y_k)$。那么使用数学表达式，则如下:
$$\hat{x}=\underset{x}{\mathrm{argmax}}p(x|v,y)\text{\hspace{1em}(07)}$$上式表达的意思是，就是在已知 $v=(\check{x_0},v_{1:k})=(\check{x_0},v_1,\cdots ,v_k)$ 与 $y=y_{0:k}=(y_0,\cdots ,y_k)$ 的条件下，估算出各个时刻状态量的后验估计 $\hat{x}=(\widehat{x_0},\cdots ,\widehat{x_k})$。注意，这里要求的是 $\hat{x}$ 整体最优，而不是某个时刻最优。根据联合概率与条件概率转换公式，可得如下两个等式：$$\begin{gathered} p(x,v,y)=p(x|v,y)\cdot p(y|v)\cdot p(v) \\ p(x,v,y)=p(y|v,x)\cdot p(x|v)\cdot p(v)\text{\hspace{1em}(08)} \end{gathered}$$上面两式联合得：$$p(x|v,y)=\frac{p(y|v,x)\cdot p(x|v)}{p(y|v)}\text{\hspace{1em}(09)}$$这个形式其实就是贝叶斯多条件变量形式，故$$\hat{x}=\underset{x}{\mathrm{argmax}}p(x|v,y)=\underset{x}{\mathrm{argmax}}\frac{p(y|v,x)\cdot p(x|v)}{p(y|v)}\text{\hspace{1em}(10)}$$
需要注意的一点式，上式推导过程都是基于离散形式的，若对前面知识点比较深刻，可以猜到离散与连续还是存在一定区别的。

对于批量式的最优状态估算，并不需要求解后验 $\hat{x}$ 的概率分布，只需知道 $p(x|v,y)$ 最大值即可，因为其最大值对应的 $x$ 我们即认为是 $\hat{x}$，在进一步根据上式可以知道分母 $p(y|v)$ 与 $x$ 是没有关系的，且我们是求最大值，则可舍去分母：$$\hat{x}=\underset{x}{\mathrm{argmax}}p(x|v,y)=\underset{x}{\mathrm{argmax}}p(y|v,x)\cdot p(x|v)=\underset{x}{\mathrm{argmax}}p(y|x)\cdot p(x|v)\text{\hspace{1em}(11)}$$可以看到上式子最右边等号，因为各个时刻的噪声是不相关(高斯分布中等价于独立)，所以 $p(y|x)$ 与 $p(x|v)$ 可以展开以乘积的方式表示$$p(x\mid v)=p\left(x_0\mid {\check{x}}_0\right)\prod _{k=1}^{K}p\left(x_k\mid x_{k-1},v_k\right)p(y\mid x)=\prod _{k=0}^{K}p\left(y_k\mid x_k\right)\text{\hspace{1em}(12)}$$其上推导过程是比较好理解的，也就是把相关的整合到一起，不相关的通过乘积串起来。可以看到两个部分都是=可以分解成累乘的方式，那么很容易想到使用对数的形式，变成累加如下：
$$\ln (p(y\mid x)p(x\mid v))=\ln p\left(x_0\mid {\check{x}}_0\right)+\sum _{k=1}^K\ln p\left(x_k\mid x_{k-1},v_k\right)+\sum _{k=0}^K\ln p\left(y_k\mid x_k\right)\text{\hspace{1em}(13)}$$$核心要点：$在前面的博客有提到过，两个高斯分布相乘,得到的结果仍然为高斯分布，有兴趣的朋友可以具体百度或者谷歌一下找到相关证明。要令上式取得最大值，首先来分析其第一项 $\ln p\left(x_0\mid {\check{x}}_0\right)$，这里要知道的是，需要把其 $x_0$ 看作是变量，因为 $0\sim k$ 时刻的所有状态变量 $x=x_{0:k}=(x_0,\cdots ,x_k)$ 都是变量。即 $\ln p\left(x_0\mid {\check{x}}_0\right)$ 取最大值，其含义就是说基于 ${\check{x}}_0$ 的条件下，$x_0$ 取何值时，其概率最大。这里的概率 $p$ 是符合高斯分布的，其均值就是 ${\check{x}}_0$，带入高斯分布公式得：$$\begin{array}{rl}\ln p\left(x_0\mid {\check{x}}_0\right)=& -\frac{1}{2}{\left(x_0-{\check{x}}_0\right)}^{\mathrm{T}}{\check{P}}_0^{-1}\left(x-{\check{x}}_0\right)-\underset{\text{与 }x\text{ 无关 }}{\underbrace{\frac{1}{2}\ln \left((2\pi {)}^N\det {\check{P}}_0\right)}}\end{array}\text{\hspace{1em}(14)}$$同理，对另外的两项进行也同样带入到高斯分布得：$$\begin{array}{rl}\ln p\left(x_k\mid x_{k-1},v_k\right)=& -\frac{1}{2}{\left(x_k-A_{k-1}{x}_{k-1}-v_k\right)}^{\mathrm{T}}{Q}_k^{-1}\left(x_k-A_{k-1}{x}_{k-1}-v_k\right)\\ & -\underset{\text{与 }x\text{ 无关 }}{\underbrace{\frac{1}{2}\ln \left((2\pi {)}^N\det Q_k\right)}}\end{array}\text{\hspace{1em}(15)}$$$$\begin{array}{rl}\ln p\left(y_k\mid x_k\right)=& -\frac{1}{2}{\left(y_k-C_k{x}_k\right)}^{\mathrm{T}}{R}_k^{-1}\left(y_k-C_k{x}_k\right)\\ & -\underset{\text{与 }x\text{ 无关 }}{\underbrace{\frac{1}{2}\ln \left((2\pi {)}^M\det R_k\right)}}\end{array}\text{\hspace{1em}(16)}$$上面得(14)(15)(16)式，舍去 $x$ 无关项，定义：$$\begin{array}{l}{J}_{v,k}(x)=\{\begin{array}{ll}\frac{1}{2}{\left(x_0-{\check{x}}_0\right)}^{\mathrm{T}}{\tilde{P}}_0^{-1}\left(x_0-{\check{x}}_0\right),& k=0\\ \frac{1}{2}{\left(x_k-A_{k-1}{x}_{k-1}-v_k\right)}^{\mathrm{T}}{Q}_k^{-1}\left(x_k-A_{k-1}{x}_{k-1}-v_k\right),& k=1,\cdots ,K\end{array}\\ J_{y,k}(x)=\frac{1}{2}{\left(y_k-C_k{x}_k\right)}^{\mathrm{T}}{R}_k^{-1}\left(y_k-C_k{x}_k\right),k=0,\cdots ,K\end{array}$$于是目标函数变为求这个式得最小化：$$\hat{x}=\arg \underset{x}{\min }J(x)J(x)=\sum _{k=0}^K\left(J_{v,k}(x)+J_{y,k}(x)\right)\text{\hspace{1em}(17)}$$这个问题就是参见的无约束最少二乘问题，可以看 $J_{v,k}(x)$、$J_{y,k}(x)$ 本质上就是状态方程与 观测方程误差项总合。

四、结语

该篇博客，不仅对贝叶斯滤波理论基础进行了梳理，还额外提及到了离散形式下的批量优化。上面举例的形式是一种极端的形式，即考虑 $0\sim k$ 时刻的所有数据，可想而知，其应用过程是十分耗时的。这种方式称为最大后验估计(Maximum A Posteriori MAP)，需要注意，其是基于 LG 系统进行推断的。

在实际应用中，也可以只考虑到一个小段时间，进行优化求解，如 $i\sim k$ 时刻。另外，还有一些批量优化处理与卡尔曼递推联合起来，一起使用的方法，若后续时间充裕，会为大家分析讲解一下。对贝叶斯滤波有了基本了解之后，下一篇博客我们就分析卡尔曼滤波了。