【C++】STL容器适配器——stack类的使用指南（含代码使用）（17）

前言

大家好吖，欢迎来到 YY 滴C++系列，热烈欢迎！本章主要内容面向接触过C++的老铁
主要内容含：

欢迎订阅 YY滴C++专栏！更多干货持续更新！以下是传送门！

一、stack 类——基本介绍

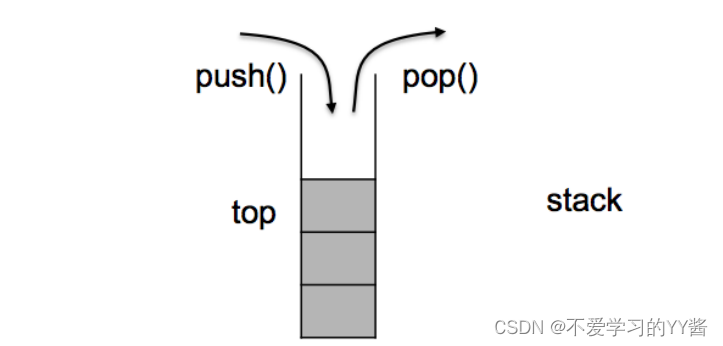
stack是一种容器适配器，专门用在具有后进先出操作的上下文环境中，其删除只能从容器的一端进行元素的插入与提取操作。
stack是作为容器适配器被实现的，容器适配器即是对特定类封装作为其底层的容器，并提供一组特定的成员函数来访问其元素，将特定类作为其底层的，元素特定容器的尾部(即栈顶)被压入和弹出。
stack的底层容器可以是任何标准的容器类模板或者一些其他特定的容器类，这些容器类应该支持以下操作：（empty：判空操作 back：获取尾部元素操作 push_back：尾部插入元素操作 pop_back：尾部删除元素操作)
标准容器vector、deque、list均符合上述四种需求，默认情况下，如果没有为stack指定特定的底层容器，默认情况下使用deque。

二、stack 类——使用环境准备

在使用string类时，必须包含#include<stack> #include<iostream>以及展开命名空间using namespace std;

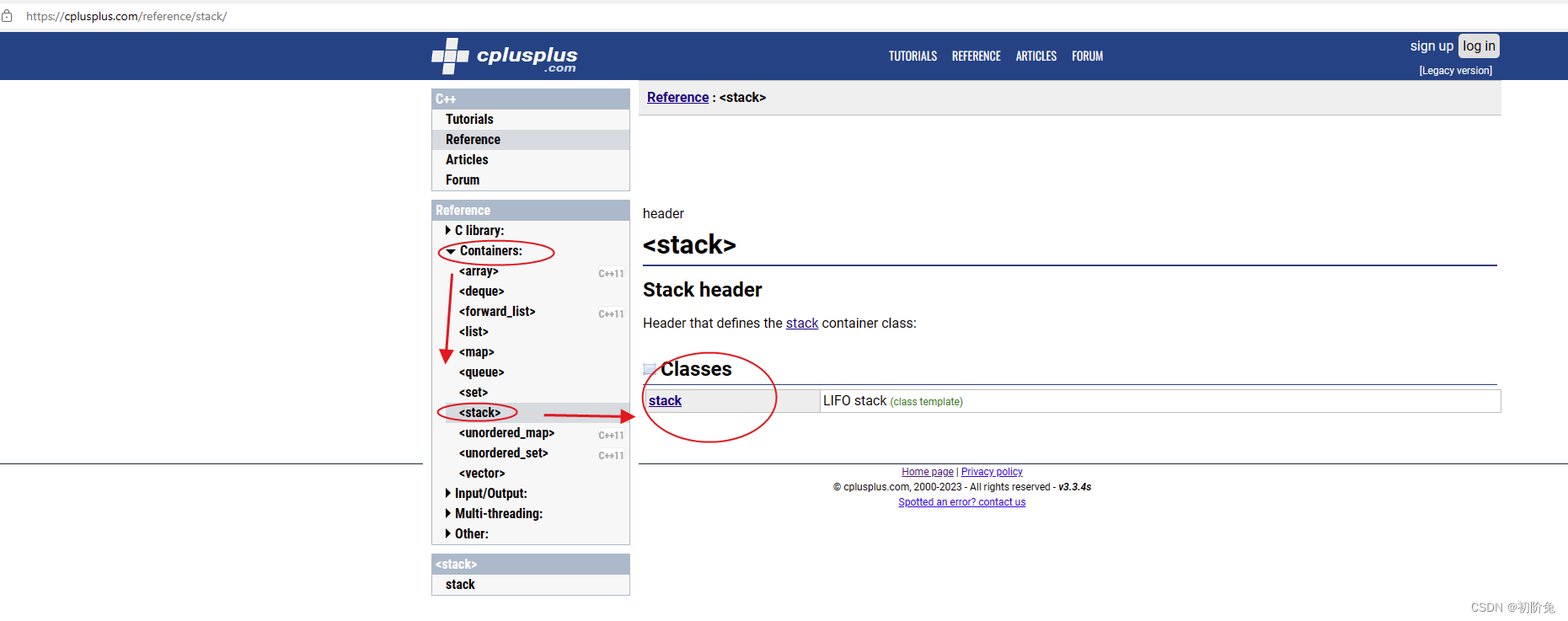
三、stack类——文档查看

查看所有接口网站：https://cplusplus.com

四、stack 类——常用接口

函数	功能说明
stack()	构造空的栈
empty()	检测stack是否为空
size()	返回stack中元素的个数
top()	返回栈顶元素的引用
push()	将元素val压入stack中
pop()	将stack中尾部的元素弹出

1).stack 基本使用场景

void test_stack_queue()
{
//创建一个栈以后，不断压入元素stack<int> st;st.push(1);st.push(2);st.push(3);st.push(4);//取栈顶元素后，出栈顶元素while (!st.empty()){cout << st.top() << " ";st.pop();}cout << endl;deque<int> dq;dq.push_back(1);dq.push_back(2);dq.push_back(3);dq.push_back(4);dq.push_back(5);dq.push_back(6);for (size_t i = 0; i < dq.size(); i++){cout << dq[i] << " ";}cout << endl;
}

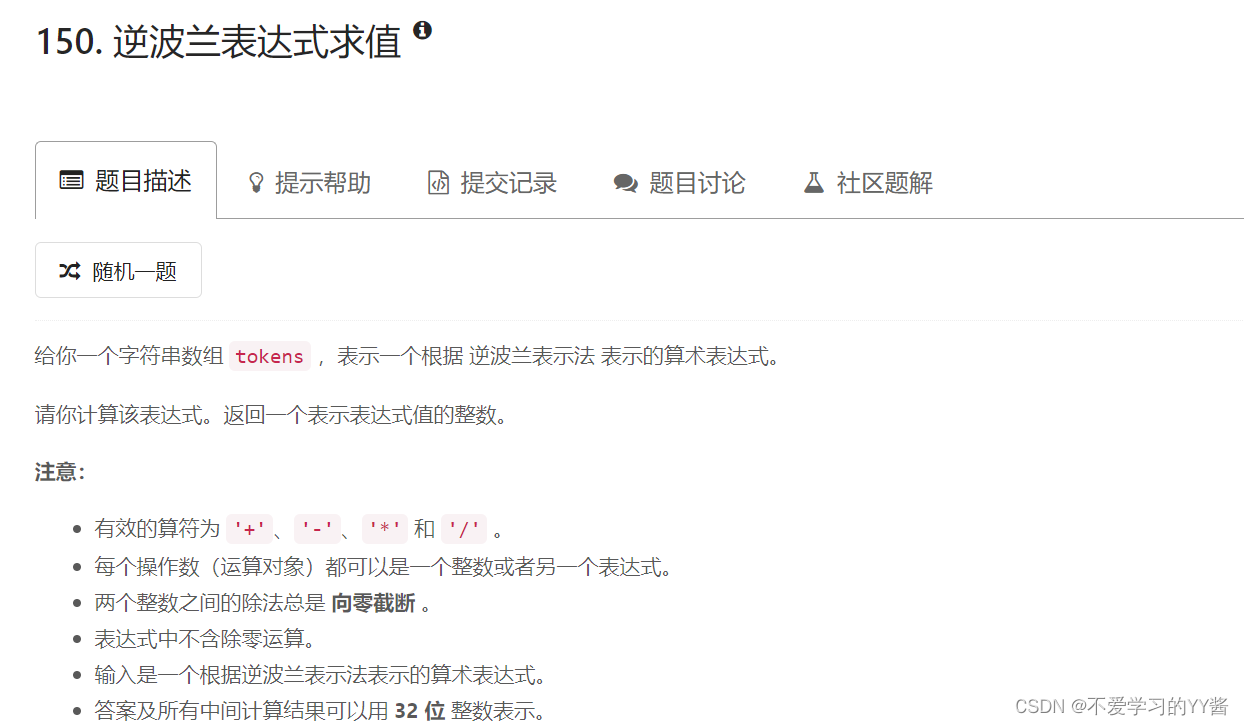
五、stack类——例题应用（逆波兰表达式求值）

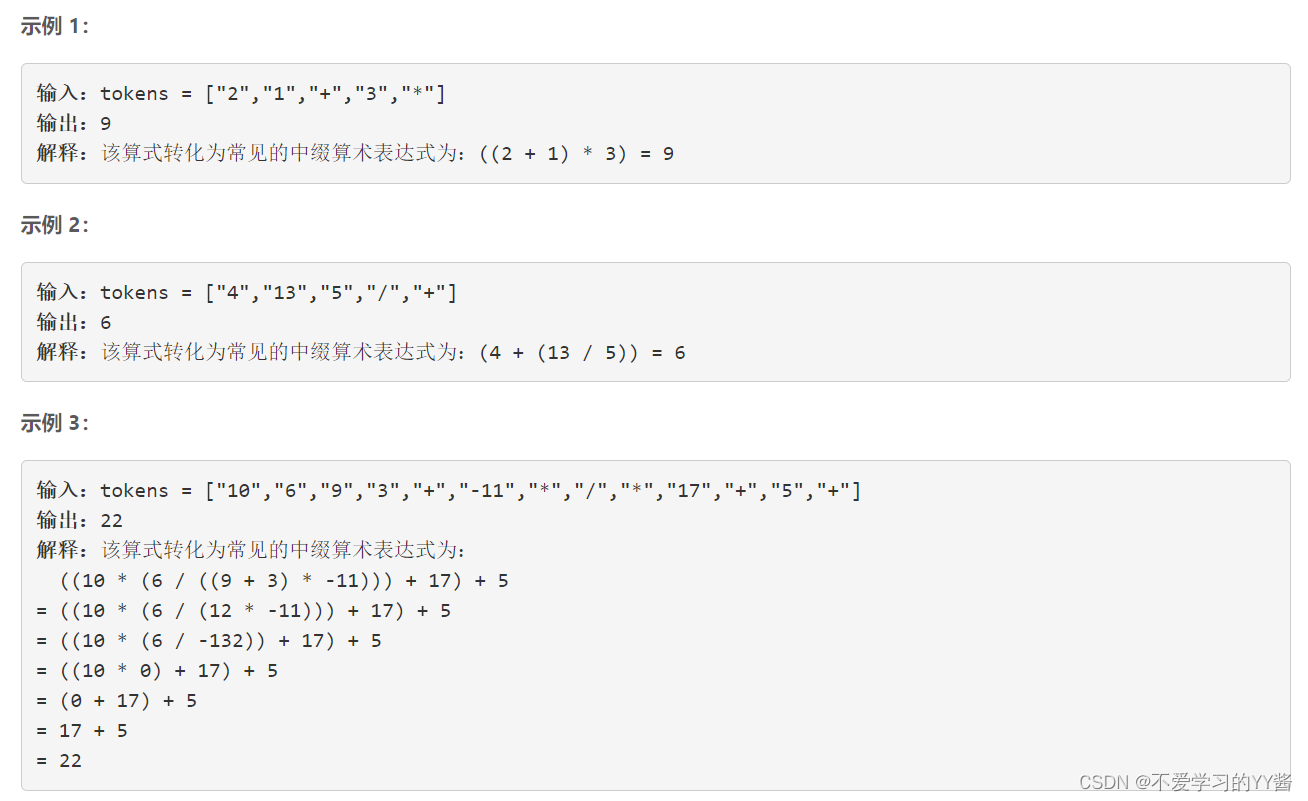
题目所示：

题解：
用传统C语言做法：

注意要点：

不可以直接对str里的数据进行switch case，因为switch case 要求其中的操作数是整型，所以必须确保栈里面的数据要么是经过atoi后的符号，要么是将整型划分为左右操作数以后出栈后剩下的符号；

class Solution {
public:int evalRPN(vector<string>& tokens){stack<int> s;for (size_t i = 0; i < tokens.size(); ++i){string& str = tokens[i];// str为数字if (!("+" == str || "-" == str || "*" == str || "/" == str)){s.push(atoi(str.c_str()));}else{// str为操作符int right = s.top();s.pop();int left = s.top();s.pop();switch (str[0]){case '+':s.push(left + right);break;case '-':s.push(left - right);break;case '*':s.push(left * right);break;case '/':// 题目说明了不存在除数为0的情况s.push(left / right);break;}}}return s.top();}
};