一、说明

图片由作者根据 DALL-E 3 的输出编辑而成。
在这篇博文中,我们证明了这样一个通用推理模型的存在,至少对于知识图谱(KGs)是这样。我们创建了 ULTRA,这是一个单一的预训练推理模型,可推广到任意实体和关系词汇表的新 KG,作为任何 KG 推理问题的默认解决方案。
这篇文章基于我们最近的论文(预印本),并与 Xinyu Yuan (Mila)、Zhaocheng Zhu (Mila) 和 Bruno Ribeiro ( Purdue / Stanford) 共同撰写。在 Twitter 上关注 Michael、Xinyu、Zhaocheng 和 Bruno,获取更多 Graph ML 内容。
二、大纲
- 为什么KG表征学习卡在2018年
- 理论:是什么使模型具有归纳性和可转移性?
- 理论:多关系图中的等方差
- Ultra:KG推理的基础模型
- 实验:即使在零样本推理中也最好,缩放行为
- 代码、数据、检查点
三、为什么KG表征学习卡在2018年
自 2018 年以来,预训练微调范式一直伴随着我们,当时 ELMo 和 ULMFit 首次显示出有希望的结果,后来它们被 BERT 和 GPT 巩固。
在大型语言模型 (LLM) 和更通用的基础模型 (FM) 时代,我们通常有一个单一模型(如 GPT-4 或 Llama-2)在大量数据上进行预训练,并且能够以零样本方式执行各种语言任务(或至少在特定数据集上进行微调)。如今,多模态 FM 甚至在同一模型中支持语言、视觉、音频和其他模态。
在 Graph ML 中,情况略有不同。 特别是,到 2023 年底,KG 的表征学习是怎么回事?这里的主要任务是边缘级的:
- 实体预测(或知识图谱完成):给定一个头节点和关系,对图中所有可能成为真尾的节点进行排名。
(h,r,?) - 关系预测:给定两个节点,预测它们之间的关系类型
(h,?,t)
事实证明,到目前为止,它一直在 2018 年之前的某个地方。关键问题是:
每个 KG 都有自己的一组实体和关系,没有单个预训练模型可以转移到任何图形。
例如,如果我们看一下Freebase(谷歌知识图谱背后的KG)和维基数据(最大的开源KG),它们具有完全不同的实体集(86M vs 100M)和关系(1500 vs 6000)。目前的KG表示学习方法是否有希望在一个图上训练并转移到另一个图上?
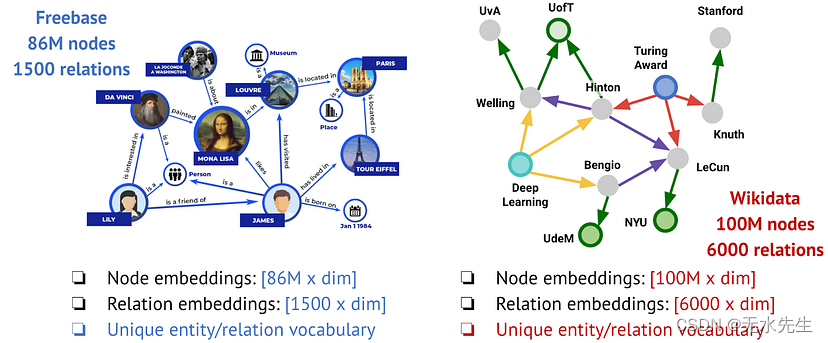
Freebase和维基数据的不同词汇。图片由作者提供。
❌ 经典的转导方法(如 TransE、ComplEx、RotatE 和数百种其他基于嵌入的方法)从训练图中学习一组固定的实体和关系类型,甚至无法支持添加到同一图中的新节点。基于浅层嵌入的方法不会转移(事实上,我们认为除了一些学生项目练习之外,开发此类方法已经没有意义了)。
🟡 归纳实体方法(如 NodePiece 和 Neural Bellman-Ford Nets)不学习实体嵌入。相反,它们将训练(可见)和新推理(看不见)节点参数化为固定关系的函数。由于他们只学习关系嵌入,因此它确实允许他们转移到具有新节点的图形,但转移到具有不同关系的新图形(例如Freebase到Wikidata)仍然遥不可及。
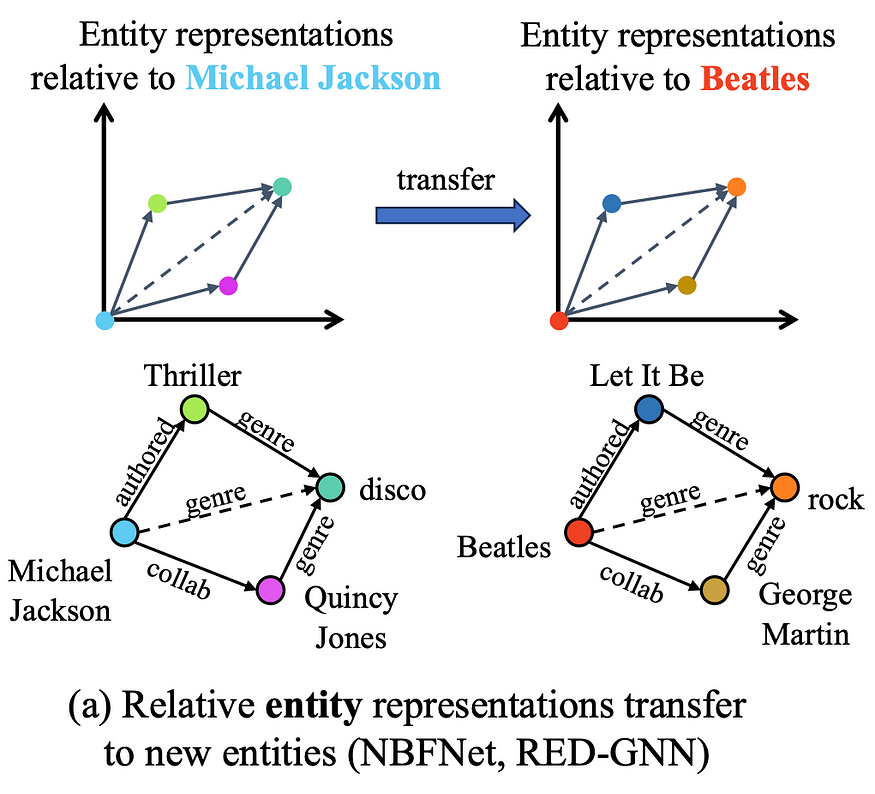
相对实体表示支持归纳 GNN。 图片由作者提供。
如果在推理时同时具有新的实体和关系(全新的图形),该怎么办?如果你不学习实体或关系嵌入,那么理论上是否可能进行转移?那么让我们来看看这个理论。
四、理论:是什么使模型具有归纳性和可转移性?
让我们更正式地定义设置:
- KG 是具有任意节点集和关系类型的有向多关系图
- 图到达时没有特征,也就是说,我们不假设实体和关系的文本描述(或预先计算的特征向量)的存在。
- 给定一个查询(head、relation、?),我们希望对底层图(推理图)中的所有节点进行排名,并最大限度地提高返回真实尾部的概率。
- 转导设置:在训练和推理时,节点和实体的集合是相同的。
- 归纳(实体)设置:关系集必须在训练时固定,但节点在训练和推理时可以不同
- 归纳(实体和关系)设置:在推理时允许新的看不见的实体和关系
神经网络学会了什么才能泛化到新数据?主要参考文献——Bronstein、Bruna、Cohen 和 Veličković 所著的《几何深度学习》一书——认为这是一个对称性和不变性的问题。
基础模型中的可学习不变性是什么?LLM 在固定的标记词汇表(子单词单位、字节,甚至是随机初始化的向量,如 Lexinvariant LLM 中)进行训练,视觉模型学习投影图像补丁的函数,音频模型学习投影音频补丁。
多关系图的可学习不变性是什么?
首先,我们将介绍标准齐次图中的不变性(等方差)。
标准(单)排列等变图模型:当早期的 GNN 工作(Scarselli 等人,2008 年,Xu 等人,2018 年,Morris 等人,2018 年)表明,假设顶点 ID 是任意的,图上的归纳任务受益匪浅,因此如果我们重新分配顶点 ID,图模型的预测应该不会改变。这称为节点 ID 上神经网络的排列等方差。这种认识引起了极大的兴奋,并产生了大量新颖的图表示方法,因为只要神经网络与节点 ID 排列等变,我们就可以将其称为图模型。
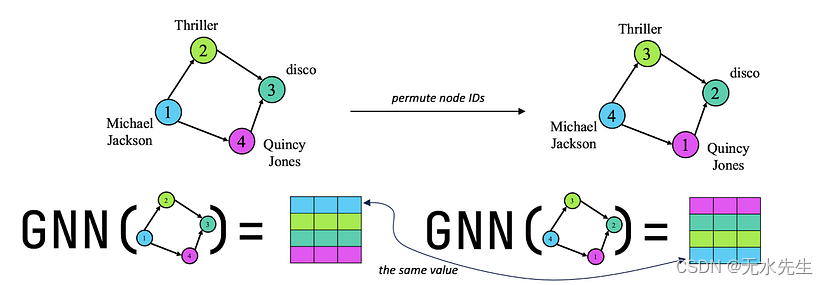
单关系图。GNN 与节点排列等变:即使在重新标记节点 ID 后,Michael Jackson 的节点向量也将具有相同的值。图片由作者提供。
节点 ID 上的排列等方差允许 GNN 以感应方式(零样本)将从训练图中学习到的模式转移到另一个(不同的)测试图。这是等方差的结果,因为神经网络不能使用节点 ID 来生成嵌入,因此它必须使用图结构。这创造了我们所知道的图形中的结构表示(参见 Srinivasan 和 Ribeiro (ICLR 2020))。
五、多关系图中的等方差
现在,图中的边可能具有不同的关系类型——这些图是否有任何 GNN 理论?
1️⃣ 在我们之前的工作中,Weisfeiler 和 Leman Go Relational(与 Pablo Barceló、Christopher Morris 和 Miguel Romero Orth,LoG 2022 合作),我们推导出了关系 WL——一种用于多关系图的 WL 表达性层次结构,更侧重于节点级任务。 Huang 等人 (NeurIPS 2023) 的伟大后续工作将该理论扩展到使用关系 WL 将预测、形式化条件消息传递和逻辑表达联系起来。✍️ 让我们记住条件消息传递 - 我们稍后会用到它 - 它可以证明可以提高链路预测性能。
提议添加由入/出边缘方向引起的全局读出向量类似于 Emanuele Rossi 等人最近关于研究均匀 MPNN 方向性的工作(有关详细信息,请阅读 Medium 上的博客文章)。尽管如此,这些作品并没有设想到甚至在测试时甚至看不到关系的情况。
2️⃣ 双排列等变(多关系)图模型:最近,Gao et al. 2023 提出了多关系图的双等方差概念。双重等方差迫使神经网络与节点 ID 和关系 ID 的联合排列等变。这确保了神经网络学习节点和关系之间的结构模式,从而允许它归纳(零样本)将学习到的模式转移到另一个具有新节点和新关系的图上。
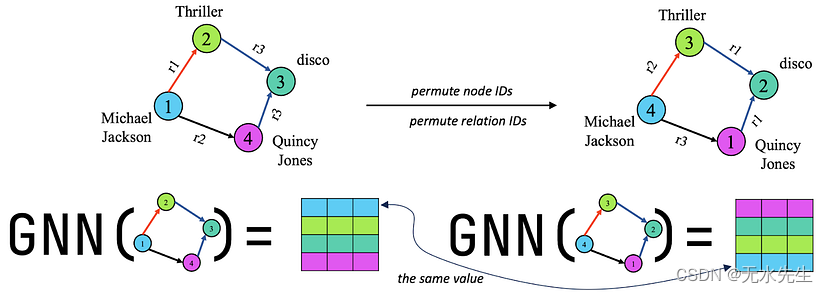
多关系图中的双等方差。同时置换节点 ID 和关系 ID 不会更改关系结构。因此,输出节点状态应相同(但有排列)。图片由作者提供。
➡️ 在我们的工作中,我们发现了关系交互的不变性,也就是说,即使关系身份不同,它们的基本交互作用也保持不变,并且这些基本交互作用可以通过关系图来捕捉。在关系图中,每个节点都是原始图中的关系类型。如果原始图中具有这些关系类型的边入射(即,它们共享一个头节点或尾节点),则此图中的两个节点将被连接。根据入射率,我们在关系图中区分 4 种边类型:
- Head-to-head (h2h) — 两个关系可以从同一个头实体开始;
- Tail-to-head (t2h) — 一个关系的尾部实体可以是另一个关系的头部;
- Head-to-tail (h2t) — 一个关系的头部实体可以是另一个关系的尾部;
- Tail-to-tail (t2t) — 两个关系可以具有相同的尾部实体。

原始图中的不同入射模式在关系图中产生不同的交互作用。最右边:示例关系图(为清楚起见,省略了反边)。图片由作者提供
关系图的一些不错的属性:
- 它可以从任何多关系图(具有简单的稀疏矩阵乘法)构建
- 这 4 个基本相互作用永远不会改变,因为它们只是编码基本拓扑——在有向图中,总会有头节点和尾节点,而我们关系将具有这些入射模式
从本质上讲,学习关系图上的表示可以转移到任何多关系图上!这是可学习的不变性。
事实上,可以证明(我们已经在研究形式证明,这将在即将到来的工作😉中提供)通过关系图中的相互作用来表示关系是一个双等变模型!这意味着学习的关系表示独立于身份,而是依赖于关系、节点以及节点和关系之间的联合交互。
六、Ultra:KG推理的基础模型
有了所有理论基础的支持,我们现在准备引入 ULTRA。
ULTRA 是一种统一、可学习和可转移的图形表示方法。ULTRA 利用关系图的不变性(和等方差)及其基本交互作用,并应用条件消息传递来获得相对关系表示。也许最酷的事实是
单个预训练的 ULTRA 模型可以在任何可能的多关系图上运行 0 次推理,并在任何图上进行微调。
换句话说,ULTRA几乎是一个基础模型,可以在任何图形输入上运行推理(具有良好的性能),并在任何感兴趣的目标图形上进行微调。
ULTRA 的关键组成部分是从关系图构建的相对关系表示。给定一个查询(Michael Jackson,genre,?),我们首先用全一向量初始化关系图中的流派节点(所有其他节点都用零初始化)。运行 GNN,关系图的节点嵌入以流派节点为条件——这意味着每个初始初始化的关系将有自己的关系特征矩阵,这从许多理论和实践方面都非常有帮助!
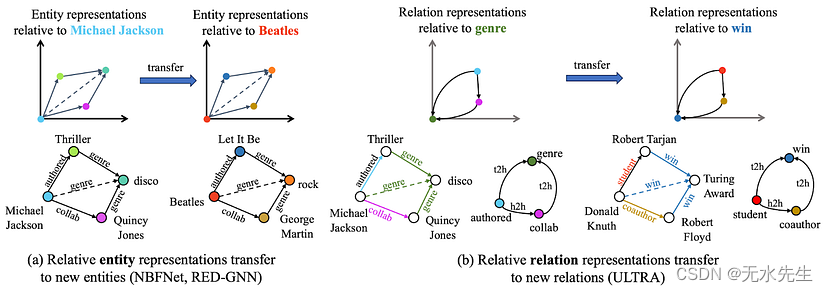
ULTRA采用相对关系表示(关系图上的标记技巧),使得每个关系(例如,“流派”)都有自己独特的所有关系表示矩阵。图片由作者提供。
实际上,给定输入 KG 和 (h, r, ?) 查询,ULTRA 将执行以下操作:
- 关系图的构建;
- 从在关系图上传递 GNN 的条件消息中获取关系特征(以初始化的查询关系 r 为条件);
- 将获得的关系表示用于以初始化头节点 h 为条件的归纳链路预测器 GNN;
步骤 2 和 3 是通过对神经 Bellman-Ford 网络 (NBFNet) 的略微不同的修改来实现的。ULTRA 只学习 4 种基本相互作用(h2t、t2t、t2h、h2h)和 GNN 权重的嵌入——总体上相当小。我们试验的主要模型只有 177k 个参数。
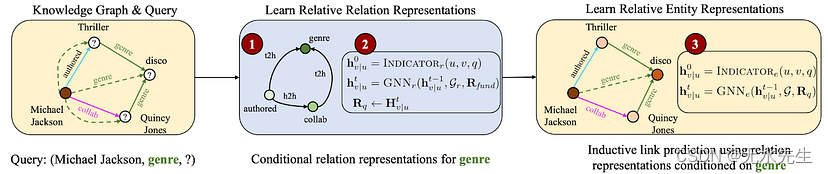
ULTRA采取的三个主要步骤:(1)建立关系图;(2)运行条件消息传递关系图,得到相对关系表示;(3)在实体级别上将这些表示用于归纳链接预测器GNN。图片由作者提供。
七、实验:即使在零样本推理和微调中也最好
我们在基于 Freebase、Wikidata 和 Wordnet 的 3 个标准 KG 上预训练了 ULTRA,并在 0+ 个其他不同大小的 KG 上运行了 50 次链路预测,这些 KG 来自 1k — 120k 节点和 2k 边缘 — 1.1M 边缘。
在具有已知 SOTA 的数据集中取平均值,单个预训练的 ULTRA 模型在 0 次推理模式下比在每个图🚀上专门训练的现有 SOTA 模型更好 微调可将性能进一步提高 10%。特别令人惊讶的是,单个经过训练的 ULTRA 模型可以扩展到如此不同大小的图形(节点大小相差 100 倍,边大小相差 500 倍),而众所周知,GNN 存在大小泛化问题(参见 Yehudai 等人的杰出著作,ICML 2021 和 Zhou 等人的杰出作品,NeurIPS 2022)。
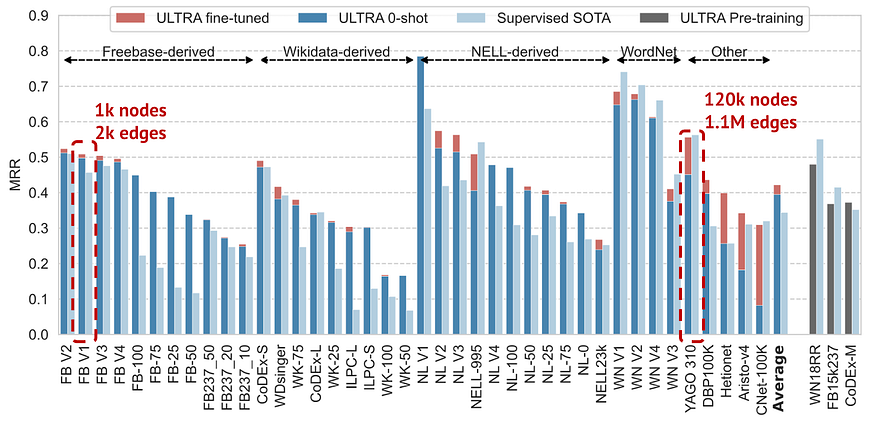
即使在 0 次推理模式下,单个预训练的 ULTRA 也比在特定图形上端到端训练的监督 SOTA 模式更好(查看 Average 列)。微调可进一步提高性能。图片由作者提供
🙃 事实上,在 57 张经过测试的图表中,我们用完了 KG 来测试 ULTRA。因此,如果您在某个地方隐藏了全新的基准测试,请告诉我们!
八、缩放行为
我们可以通过在预训练组合中添加更多图表来进一步提高零样本性能,尽管我们在 4+ 图表上训练后确实观察到一定的性能饱和度。
Scaling Laws 教会预测,在更定性的数据上训练更大的模型会获得更好的性能,因此这绝对在我们的议程上。
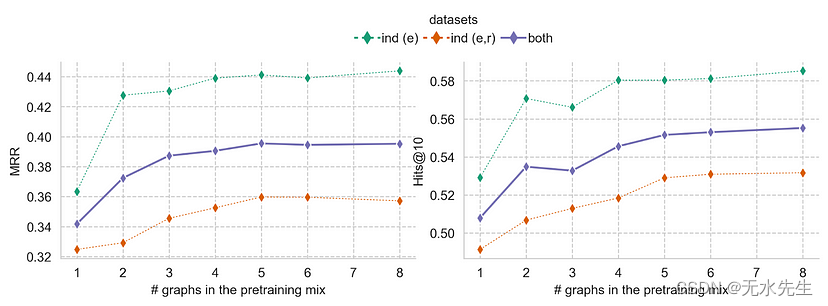
零样本性能随着预训练组合中更多样化的图形而提高。图片由作者提供。
九、结论:代码、数据、检查点
所以KG推理的基础模型终于来了,我们已经超过了2018年的门槛!单个预训练的 ULTRA 模型可以对来自任何域的任何 KG(多关系图)执行链接预测。您实际上只需要一个具有 1 种以上边缘类型的图形即可开始。
📈 实际上,ULTRA 在 0 次模式下已经在各种 KG 基准测试中表现出非常有希望的性能,但您可以通过短暂的微调进一步提高性能。
我们在 GitHub 上提供了所有代码、训练数据和预训练模型检查点,因此您可以立即开始对数据运行 ULTRA!
📜 预印本:arxiv
🛠️ 代码、数据:Githtub 存储库
🍪 检查点:Github 存储库中的 2 个检查点(每个检查点 2 MB)
🌎 项目网址:这里
作为结束语,KG推理只是推理领域中许多有趣问题的一小部分,而且大多数仍然没有一个通用的解决方案。我们相信KG推理的成功将带来其他推理领域的更多突破(例如,我们最近发现LLM实际上可以学习和运用文本规则)。让我们对推理的未来保持乐观!






![[Linux] GRUB引导 学习笔记(一)](https://img-blog.csdnimg.cn/img_convert/d98a230bc7537e8d21c0ea8930418f5b.png)