Fourier分析导论——第4章——Fourier级数的一些应用(E.M. Stein R. Shakarchi)

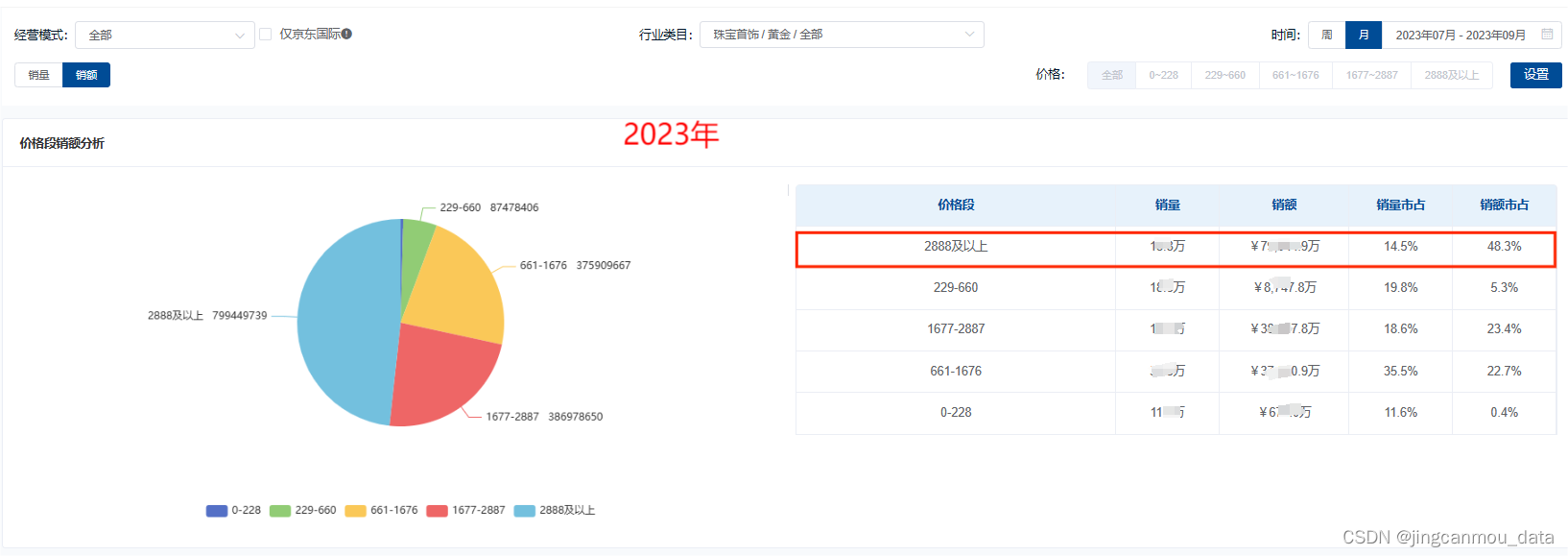
第 4 章傅里叶级数的一些应用

Fourier series and analogous expansions intervene very

naturally in the general theory of curves and surfaces.

In effect, this theory, conceived from the point of view

of analysis, deals obviously with the study of arbitrary

functions. I was thus led to use Fourier series in sev-

eral questions of geometry, and I have obtained in this

direction a number of results which will be presented

in this work. One notes that my considerations form

only a beginning of a principal series of researches,

which would without doubt give many new results.

(Fourier级数和类似的展开非常自然地介入了曲线和曲面的一般理论。事实上，从分析的角度来看，这个理论显然是处理任意函数的研究。因此，我被引向在几个几何问题中使用Fourier级数，并且我在这个方向上获得了许多成果，这些成果将在本文中展示。有人指出，我的考虑只是一系列主要研究的开始，这些研究无疑会产生许多新的成果。)

----------------------------------------------------------------------------- A. Hurwitz[húəvits], 1902

在前面的章节中，我们介绍了一些关于Fourier分析的基本事实，这是由物理学中出现的问题引起的。弦的运动和热的扩散是自然地导致Fourier级数函数展开的两个例子。我们接下来建议让读者对Fourier分析的更广泛影响有所了解，并说明这些想法如何延伸到数学的其他领域。尤其要考虑以下三个问题：

I. 在所有位于实数平面 $\mathbb{R}^{2}$ (译注：手写体双线字母)中的长度为𝓁(译注：字母l的数学体细体)的简单封闭曲线中，哪一个封闭曲线围合的面积最大？

II. 已知一个非比数 γ (译注：希腊字母wa-mma小写)，关于数例 nγ (n = 1,2,3,...)的小数部分的分布，我们可以说些什么？

III. 存在处处不可微的连续函数吗？

第一个问题本质上显然是几何问题，乍一看似乎与Fourier级数关系不大。第二个问题介于数论和动力系统研究之间，并为我们提供了遍历性(ergodicity)思想的最简单示例。”第三个问题虽然本质上是分析问题，但在最终发现解决方案之前触动了(resisted)许多尝试。值得注意的是，这三个问题都可以通过使用Fourier级数非常简单直接地得到解决。

在本章的最后一节，我们将回到一个引起我们最初动机的问题。我们考虑圆周上的时间相关的热传导方程。在这里，我们的调查将引导我们找到针对这个圆的重要而神秘的(enigmatic)热内核。然而，在我们应用Poisson求和公式(我们将在下一章中进行应用)之前，将无法完全理解围绕其基本属性的奥秘(mysteries)。

1. 等周不等式(The isoperimetric inequality)

令 Γ(译注：希腊字母wa-mma大写)表示平面上不与其自身相交叉(intersect)的封闭曲线。加外，令 𝓁 表示 Γ 的长度，并且令 𝒜 (译注：字母 A 的数学体细体，LaTex 宏 \mathcal{A})表示 $\mathbb{R}^{2}$ 平面中由 Γ 围合的界内区域的面积。现在的问题是，针对已知的曲线长度 𝓁 确定使用面积 𝒜 最大化的曲线 Γ 的表达式(如果这样的曲线存在)。

-----------------------------------------------------图 1. 等周(等周长)问题----------------------------------------

一些实验(experimentation)和深思(reflection)表明这个解应该是一个圆。可以通过以下启发式(heuristic)考虑得出该结论。这条曲线可以被认为是平放在桌面上的一条闭合的弦(string)。如果弦所围合的区域不是凸面(convex)(比如)，则可以使部分弦变形(deform)并增加它所围合的面积。此外，通过一些简单的例子，可以说服自己，曲线在某些部分越“扁平(flatter)”，围合区域的效率就越低。因此我们想最大化曲线在每个点的“圆度(roundness)”。

尽管圆是正确的猜想结果，但是，要在数学上精确地表达这种思想却是一件困难的事。

我们给出的等周问题解的关键思想包括针对Fourier级数应用Parseval恒等式。然而，在我们尝试解决这个问题之前，我们必须首先定义简单闭合曲线的概念、它的长度，以及它所围合的区域的面积。

1.1. 曲线、长度及其面积

一条参数化的 γ 曲线是一个映射 $\gamma :[a,b] \rightarrow \mathbb{R}^{2}$ 。

在平面上，γ 的图像是一个点的集合，我们称其为一条曲线(curve)，并用希腊字母 Γ 表示。如果曲线 Γ 其自身不交叉，则曲线很简单，并且，如果其两个端点叠合(coincide)，则曲线是围合的(closed)。根据以上参数化表达式，这两个条件转换成：除非满足 $s_{1}=a,s_{2}=b$ ,且有 $\gamma(a) = \gamma(b)$ ，否则 $\gamma(s_{1}) \neq \gamma(s_{2})$ 。我们可以将 γ 扩展为实数域 ℝ 上周期为 b – a 的周期函数，并将 γ 视为圆周上的函数。此外，我们总是施加某些平滑条件在我们的曲线上，假设 γ 是 $C^{1}$ 类平滑曲线，其一阶导数 γ’ 满足条件 γ’ ≠ 0。这些条件合起来确保了曲线 Γ 在其上每一点具有定义良好的切线，且切线随着曲线上点的变化而连续变化。此外，参数化的 γ 曲线随着 s 从 a 行进到 b 的过程中，会在 Γ 上产生一个可变的方向。

任何一个 $C^{1}$ 类双射映射(bijective mapping) $s: [c,d]\rightarrow[a,b]$ 都会引起 Γ 的另一个参数化表达式，用公式表示为 $\eta(t) = \gamma(s(t))$ 。显然，γ 是围合的且简单的这两个条件与所选取的参数无关。此外，如果对于所有的 t ，s ’(t) > 0 ,则我们称这两个参数化表达式 γ 和 η 是等价的；这意味着 η 和 γ 在曲线上产生的方向是相同的。然而，假如 s ’(t) < 0，则 η 产生相反的方向。

如果 γ 的参数化表达式为 $\gamma(s) = (x(s),y(s))$ , 则曲线 Γ 的长度定义为

$\displaystyle \ell = \int_{a}^{b}|\gamma^{'}(s)|ds=\int_{a}^{b}[x^{'}(s)^{2}+y^{'}(s)^{2}]^{1/2}ds$ 。

曲线 Γ 的长度对曲线而言是一个固有的(intrinsic)概念，不取决于其参数表达式。为了理解这个事实，假设 $\gamma(s(t)) = \eta(t)$ ，则变量变化公式和链式法则意味着

$\displaystyle \int_{a}^{b}|\gamma^{'}(s)|ds=\int_{c}^{d}\left |\gamma^{'}(s(t))\right | \left | s^{'}(t) \right |dt=\int_{c}^{d}\left | \eta^{'}(t)dt \right |$ ，

这个结果正如预期。

在下面证明这个定理的过程中，我们将使用针对曲线 Γ 的一个特殊参数化类型。假如对于所有的 s，有 |γ (s)| = 1，则我们称 γ 由弧长(arc-length)参数化。这意味着 γ (s) 以固定的速度行进，最终结果便是，Γ 的长度正好等于 b – a 。因此，经过可行的额外转换之后，就得到了一个定义在闭区间[0, 𝓁]上的按弧长参数化的表达式。任意曲线都允许用弧长进行参数化(练习1)。

现在我们转向等周长问题。

尝试给出由简单闭合曲线 Γ 围合区域的面积 𝒜 的准确公式引发了话多棘手的(tricky)问题。在各种简单的面积计算场景中，由下面熟悉的积分公式给出的面积计算公式是显而易见的：

(1) $\displaystyle \begin{array}{rl} \mathcal{A} & = \frac{1}{2} \left | \int_{\Gamma}^{}(xdy - ydx) \right | \\ &= \frac{1}{2} \left | \int_{a}^{b} \left [x(s)y^{'}(s)+y(s)x^{'}(s)\right ]ds \right | \end{array}$ ；

参见，例如，练习3 。因此，在公式化我们的结论的时候，我们将采用容易的权宜之计(expedient)，将(1)作为面积的定义。这种方法允许我们快速而简洁地证明等周不等式。在定理证明之后可以找到此简化未解决的问题列表。

1.2. 等周不等式的表述和证明

定理1.1 假如 Γ 是平面 $\mathbb{R}^{2}$ 上的一条长度为 𝓁 的闭合曲线，令 𝒜 表示由这条曲线围合的区域的面积。则

$\displaystyle \mathcal{A} \leq \frac{\ell^{2}}{4\pi}$ ,

且当且仅当 Γ 是圆的时候，等号成立。

通过观察，我们首先发现我们可以重新调整(rescale)问题。这意味着，我们可以用一个 δ > 0 的因子按随后的方式更改度量单位。考虑平面 $\mathbb{R}^{2}$ 到其自身的映射——将点(x,y)投射到(δx, δy)。观察定义曲线长度的公式可以发现，长度公式表明，如果 Γ 的长为 𝓁 ，则它在这个映射下的图像的长度为 δ𝓁 。因此，这个运算是按比例因子 δ 放大(magnifies)还是缩小(contracts) 曲线长度，这取决于 δ ≥ 1 还是 δ ≤ 1 。类似地，我们可以看到，这个映射按比例因子 $\delta^{2}$ 放大(或缩小)围合区域的面积。通过取 δ = 2π/𝓁 ，我们可以看到，这足够证明，假如 𝓁 = 2π ，则 𝒜 ≤ π ，且仅当 Γ 是一个圆的时候等式成立。

令 $\gamma:[0,2\pi] \rightarrow \mathbb{R}^{2}$ 且 γ (s) = (x(s),y(s)) 为用曲线 Γ 的弧长表示参数的参数化表达式，即，对于所有 s∈[0，2π],有 $x^{'}(s)^{2}+y^{'}(s)^{2}=1$ 。这意味着，

(2) $\displaystyle \frac{1}{2\pi} \int_{0}^{2\pi}\left [ x^{'}(s)^{2}+y^{'}(s)^{2} \right ]ds=1$ 。

因为曲线是闭合的，函数 x(s) 和 y(s) 是 2π 周期的，因此，我们可以考虑其Fourier级数

$x(s) \sim \sum a_{n}e^{ins}$ 和 $y(s) \sim \sum b_{n}e^{ins}$ 。

则，正如我们在第2章第2节的后面评注的那样，我们有

$x^{'}(s) \sim \sum ina_{n}e^{ins}$ 和 $y^{'}(s) \sim \sum inb_{n}e^{ins}$ 。

应用 Parseval 恒等式到 (2) 得到

(3) $\displaystyle \sum_{n-\infty}^{\infty}|n|^{2}(|a_{n}|^{2}+(|b_{n}|^{2})=1$ 。

现在应用 Parseval 恒等式的双线性形式(第3章，引理1.5)到定义 𝒜 的积分。因为 x(s) 和 y(s) 是实数值函数，我们有 $a_{n}=\overline{a_{-n}}$ 和 $b_{n}=\overline{b_{-n}}$ , 因此，我们求得

$\displaystyle \mathcal{A}=\frac{1}{2\pi} \left | \int_{0}^{2\pi}\left [ x(s)y^{'}(s)-y(s)x^{'}(s) \right ]ds \right |= \pi \left | \sum_{n=-\infty}^{\infty}n(a_{n}\overline{b_{n}}-b_{n}\overline{a_{n}}) \right |$ 。

接下来，我们观察到

(4) $\displaystyle \left | (a_{n}\overline{b_{n}}-b_{n}\overline{a_{n}}) \right | \leq 2|a_{n}||b_{n}| \leq |a_{n}|^{2}+|b_{n}|^{2}$ ,

并且，因为 $|n| \leq |n|^{2}$ ,我们可以用(3) 求得

$\displaystyle \mathcal{A} \leq \pi \sum_{n-\infty}^{\infty}|n|^{2}(|a_{n}|^{2}+(|b_{n}|^{2}) \leq \pi$ ，

正如所预期的那样。

当 𝒜 = π 时，我们从以上的论据中可以看出

$\displaystyle x(s) = a_{-1} e^{-is} + a_{0} + a_{1} e^{is}$ 和 $\displaystyle y(s) = b_{-1} e^{-is} + b_{0} + b_{1} e^{is}$ 。

因为 $|n| \leq |n|^{2}$ 且 $|n| \geq 2$ 。从前面我们知道，x(s) 和 y(s) 都是实数值的，因此， $a_{-1} = \overline{a_{1}}$ 和 $b_{-1} = \overline{b_{1}}$ 。恒等式 (3) 意味着 $\displaystyle 2(|a_{n}|^{2}+(|b_{n}|^{2})=1$ ，因此，我们有(4)中的等式，从而我们一定有 $a_{1}=b_{1}=\frac{1}{2}$ 。我们写成

$a_{1}=\frac{1}{2}e^{i\alpha}$ 和 $b_{1}=\frac{1}{2}e^{i\beta}$ 。

$1= 2|a_{1}\overline{b_{1}}-\overline{a_{1}}b_{1}|$ 这个事实意味着 $|\sin(\alpha-\beta)| = 1$ (译注：由Euler恒乖式推出 $\displaystyle \sin(\alpha-\beta)=\left | \frac{e^{i(\alpha-\beta)}-e^{-i(\alpha-\beta)}}{2i} \right |$ ), 因此，α – β = kπ ，其中，k 是一个奇数。据此，我们求得

$x(s) = a_{0} + \cos(\alpha+ s )$ 和 $y(s) = b_{0} \pm \sin(\alpha + s )$ , 其中，y(s) 中的符号取决于(k - 1)/2 的奇偶性(parity)。我们发现，在任何情况下，Γ 是圆的时候，等号这个情况总是成立，因此，我们完成了证明。

以上给出的解(归功于1901年的Hurwitz[húəvits]提出的定理，Adolf Hurwitz,1859年3月26日～1919年11月18日，德国数学家)确定非常优雅，但很明显，留下了一些未解决的(answered)重要问题。我们把这些问题列在下面。假设 Γ 是一条简单的闭合曲线。

( $i$ ) “由 Γ 围合的区域”是如何定义的？

( $i i$ ) 这个区域的“面积”的几何定义是什么？这个定义与(1)一致吗？

( $i i i$ ) 这些结论可以推广为最广泛的与这类问题(即这些曲线是“可求长的(rectifiable)”,即，具有有限长度的曲线)相关的简单闭合曲线的通用类型吗？

事实证明，要阐明提出的这些问题，就必然与分析学中其它的重要问题产生联系。我们将在本系列的后续书籍中回到这些问题。

2. Weyl[vail]的等分布定理(Weyl's equidistribution theorem)

我们现在将来自Fourier级数的思想应用到处理非比数(irrational)属性的问题。我们首先简要讨论同余(congruence)，这是理解我们的主要定理所需的概念。

2.1. 实数对整数取模(The reals modulo the integers)

假如 x 是实数，令 [x] 为小于等于 x 的最大整数，则称这个量 [x] 为 x 的整数部分(integer part)。而 x 的小数部分(fractional part)定义为 < x > = x - [x] 。特别地，对于任意 x ∈ ℝ , < x > ∈ [0,1) 。例如，2.7 的整数和分数部分分别是 2 和 0.7 ，而 -3.4 的整数和分数部分分别是 -4 和 0.6 。

假如 $x - y \in \mathbb{R}$ ，我们可以定义 ℝ 上的一种关系，比如说，定义 x 和 y 的等价关系、或称同余关系(congruence)。则，我们可以写成

$x = y \mod \mathbb{Z}$ 或者 $x = y \mod 1$ 。

这意味着，如果两个实数相关一个整数，我们就可以识别它们。观察到，任意实数 x 与 [0,1)中唯一的数(恰好是 < x >,即 x 的小数部分)是同余的。事实上，产生一个实数对整数 ℤ 取模意味着仅关注其小数部分而忽略掉其整数部分。

现在，以实数 γ ≠ 0 开始，并观察序列，γ，2γ ，3γ ，... 。一个引人入胜的(intriguing)问题是，我们要问，如果序列对 ℤ 取模，序列会发生什么，即，如果我们观察其小数部分的序列

<γ>，<2γ> ，<3γ> ，...

会发现什么现象？

下面是一些简单的观察结果：

( $i$ ) 假如 γ 是比率数(rational),则仅有有限多个出现在 <nγ> 中的数是不同的。

( $ii$ ) 假如 γ 是非比数(irrational),则 <nγ> 中所有的数都是不同的。

事实上，对于第 ( i ) 部分，注意到，假如 γ = p/q，在序列中的前面 q 项是

< p/q >，<2 p/q > ，... <(q-1)p/q >，< q p/q> = 0 。

然后，序列开始自重复，因为

<(p + 1) q > = <1 + p/q >= < p/q >,

等等。尽管如此，更精炼的例子，请参看练习6。

此外，对于第( ii )部分，假设并非所有的数都是不同的(译注：即有的数相同)。因此，对于某些 $n_{1} \neq n_{2}$ ,我们有 $<n_{1}\gamma> = <n_{2}\gamma>$ ；则 $n_{1}\gamma - n_{2}\gamma \in \mathbb{Z}$ ，因此，γ 是比率数，这与假设矛盾。

事实上，可以证明明，假设 γ 是一个非比数，则 <nγ> 在区间[0,1)上是稠密的(dense),这是一个源自Kronecker[króunèkə] 所证明的结论(译注：Kronecker，德国数学家，逻辑学家，1823年12月7日－1891年12月29日)。换句话说，序列 <nγ> 击中[0,1)的每一个子区间(因此，它击中了如此无限的次数)。随着一个更深入的处理序列 <nγ> 的一致分布的定理引理的引出，我们将获得这个事实。

假如对于每一个 (a,b)⊂ [0,1) 的区间，

$\displaystyle \lim_{N \rightarrow \infty}\frac{\# \left \{ 1 \leq n \leq N :\xi \in (a,b) \right \}}{N}=b-a$ ,

则称区间 [0,1) 中的数列 $\xi_{1} , \xi_{2} ,... \xi_{n }$ 为等分布的(equidistributed)。其中，#A表示有限集合 A 的基数(cardinality)。这指的是，对于任意大的 N，在 (a,b) 中 n ≤ N 的这部分数 $\xi_{n}$ 等于区间(a,b)的长度对区间[0,1)的长度的比率。换句话说，序列 $\xi_{n}$

均匀地(evenly)扫过整个区间，每个子区间都获得了它的公平份额(fair share)。显然，序列的次序非常重要，正如如下两个例子所示。

例子1： 序列

$0 , \hspace{0.2cm}\frac{1}{2} ,\hspace{0.2cm} 0, \hspace{0.2cm} \frac{1}{3} ,\hspace{0.2cm} \frac{2}{3}, \hspace{0.2cm} 0 ,\hspace{0.2cm} \frac{1}{4} , \hspace{0.2cm} \frac{2}{4} ,\hspace{0.2cm} \frac{3}{4} ,\hspace{0.2cm} 0,\hspace{0.2cm} \frac{1}{5},\hspace{0.2cm} \frac{2}{5},\hspace{0.2cm}...$

似乎是均匀分布的，因为它非常均匀地经过区间[0，1)。显然，这不是一个证明，观迎读者给出其证明。对于某种程序上的相似例子，请参看练习 8 中 $\sigma = \frac{1}{2}$ 的情形。

例子2：

令 $\{r_{n}\}_{n=1}^{\infty}$ 为区间[0，1)中任意比率数的枚举(enumeration)。则，由

$\displaystyle \xi_{n}=\left \{ \begin{array}{lcr} \frac{r_{n}}{2}(n \in \mathrm{even}) \vspace{0.2cm}\\ 0(n \in \mathrm{odd}) \end{array} \right.$

定义序列不是等分布的,因为序列的一半在0处。因此，很明显，序列是稠密的。

现在，我们触及本节的主要定理。

定理 2.1 如果 γ 是非比数(irrational)，则由小数部分构成的序列 <γ>，<2γ> ，<3γ> ，... 在区间 [0，1) 上是等分布的。

特别地，<nγ> 在区间 [0，1) 是稠密的，并且，我们将Kronecker定理作为一个推论。在图 2 中，我们演示了当 $\gamma = \sqrt{2}$ ，对于 N 的 3 个不同值，点 <γ>，<2γ> ，<3γ> ，...< Nγ> 构成的集合。

----------------------------------------------图 2 当 $\gamma = \sqrt{2}$ 时的序列<γ>，<2γ> ，<3γ> ，...--------------

固定 (a,b)⊂ [0,1)并令 $\chi_{(a,b)}(x)$ 表示开区间 (a,b) 的特征函数，即，函数在开区间 (a,b)上等于1，在区间 [0,1) - (a,b) 上等于 0 。我们可以将这个函数按周期性(周期为1)扩展到实数域 ℝ 上，且仍然用 $\chi_{(a,b)}(x)$ 表示这个扩展。则，作为这个定义的结果，我们求得

$\displaystyle \# \{ 1 \leq n \leq N : <n\gamma> \in (a,b) \}=\sum_{n=1}^{N} \chi_{(a,b)}(n\gamma)$ ，

并且，定理可以重述为表达式

$\displaystyle \frac{1}{N}\sum_{n=1}^{N} \chi_{(a,b)}(n\gamma) \rightarrow \int_{0}^{1}\chi_{(a,b)}(x)dx$ ( 当 $N\rightarrow \infty$ 时 ) 。

这一步消除了计算小数部分的困难，并将数论简化为分析。

引理2.2 假如 f 是一个周期为 1 的连续函数，且 γ 是一个非比数(irrational)，则

当 $N\rightarrow \infty$ 时，

$\displaystyle \frac{1}{N}\sum_{n=1}^{N} f(n\gamma) \longrightarrow \int_{0}^{1}f(x)dx$ 。

引理的证明分 3 步进行。

第 1 步：我们首先检查当 f 是指数函数 1 , $e^{2\pi x}$ , ... , $e^{2\pi kx}$ , ... 时的这种情况下的极限有效性，假如 f = 1 ，则这个极限显然成立。假如 $f=e^{2\pi kx}$ 且 k ≠ 1，则积分等于 0。因为 γ 是非比数，我们有 $e^{2\pi kx} \neq 1$ ，因此，

$\displaystyle \frac{1}{N}\sum_{n=1}^{N} f(n\gamma)=\frac{e^{2\pi i\gamma}}{N}\frac{1-e^{2\pi ikN\gamma}}{1-e^{2\pi ik\gamma}}$ ,

当 $N\rightarrow \infty$ 时，上式趋近于 0 。

第 2 步：很显然，假如 f 和 g 满足引理，则对于任意 A，B ∈ ℂ ，A f + B g 也满足引理。因此，第 1 步意味着对于所有三角多项式，引理为真。

第 3 步：令 ε > 0 。假如 f 是任意周期为 1 的连续周期函数，选取一个三角多项式P 使得 $\displaystyle \sup_{x\in \mathbb{R}}\left | f(x)-P(x) \right | < \epsilon /3$ (根据第2章推论5.4，这是可行的)。则，根据第 1 步，对于任意大的 N，我们有

$\displaystyle \left | \frac{1}{N}\sum_{n=1}^{N} P(n\gamma)-\int_{0}^{1}P(x)dx\right | < \epsilon/3$ 。

因此，

$\displaystyle \begin{array}{rl} \displaystyle \left | \frac{1}{N}\sum_{n=1}^{N} f(n\gamma) -\int_{0}^{1}f(x)dx \right | & \leq \frac{1}{N}\sum_{n=1}^{N} \left | f(n\gamma) -P(n\gamma) \right | + \\ & \displaystyle \left | \frac{1}{N}\sum_{n=1}^{N} P(n\gamma)-\int_{0}^{1}P(x)dx\right | \\ &+ \displaystyle \int_{0}^{1}|P(x)-f(x)|dx \\ & < \epsilon \end{array}$ ，

因此，引理得证。

现在，我们可以完成定理的证明。选取两个周期为 1 的连续的周期函数 $f_{\epsilon}^{+}$ 和 $f_{\epsilon}^{-}$ ，其分别在区间[0,1)上从上限和下限趋近于函数 $\chi_{(a,b)}(x)$ ； $f_{\epsilon}^{+}$ 和 $f_{\epsilon}^{-}$ 都以 1 为界且除了在总长为 2ε 的区间以外与函数 $\chi_{(a,b)}(x)$ 一致(见图3)。

特别地， $\displaystyle f_{\epsilon}^{-} \leq \chi_{(a,b)}(x) \leq f_{\epsilon}^{+}$ 且 $\displaystyle \int_{0}^{1}f_{\epsilon}^{+}dx \leq (b-a)+2\epsilon$ 。

假如

$\displaystyle S_{N}= \frac{1}{N}\sum_{n=1}^{N} \chi_{(a,b)}(n\gamma)$ , 则，我们得到

$\displaystyle$ $\displaystyle \frac{1}{N}\sum_{n=1}^{N} f_{\epsilon}^{-}(n\gamma) \leq S_{N} \leq \frac{1}{N}\sum_{n=1}^{N} f_{\epsilon}^{+}(n\gamma)$ 。

------------------------------------------图3 函数 $\chi_{(a,b)}(x)$ 的逼近值--------------------------------------------

因此，

$\displaystyle (b-a)-2\epsilon \leq \lim_{N \rightarrow \infty}\inf S_{N}$ 且 $\displaystyle \lim_{N \rightarrow \infty}\sup S_{N} \leq (b-a)+2\epsilon$ 。

因为，对于任意 $\epsilon > 0$ , $\displaystyle \lim_{N \rightarrow \infty } S_{N}$ 存在则一定等于 $(b - a)$ ，这个表述成立。这就完成了等分布定理的证明。

推论2.3 引理 2.2 的结论对于区间[0,1]上的任意 Riemann 可积函数以及周期为 1 的连续周期函数 f 都成立。

证明：

假设 f 是实数据函数，考虑区间[0,1]的一个划分，比如， $0 = x_{0} < x_{1} < ... < x_{N} = 1$ 。接下来，定义 $\displaystyle f_{U}(x)=\sup_{x_{j-1} \leq y \leq x_{j}}$ ( 假如 $x \in [ x_{j-1} , x_{j} )$ 且 $\displaystyle f_{L}(x)=\inf_{x_{j-1} \leq y \leq x_{j}}f(y)$ (假如 $\displaystyle x \in (x_{j-1} , x_{j} )$ ) 。则，显然 $\displaystyle f_{L}(x) \leq f(x) \leq \displaystyle f_{U}(x)$ ，并且
$\displaystyle$ $\displaystyle \int_{0}^{1}f_{L}(x)dx \leq \int_{0}^{1}f(x) \leq \int_{0}^{1}f_{U}(x)dx$ 。

此外，通过使划分足够好，我们可以确保对于给定的 $\epsilon > 0$ ,有

$\displaystyle \int_{0}^{1}f_{U}(x)dx - \int_{0}^{1}f_{L}(x)dx \leq \epsilon$ 。

然而，按照这个定理

$\displaystyle \frac{1}{N}\sum_{n=1}^{N}f_{L}(n\gamma) \longrightarrow \int_{0}^{1}f_{L}(x)dx$ ,

因为每一个 $f_{L}$ 都区间上特征函数的有限线性组合；类似地，我们有

$\displaystyle \frac{1}{N}\sum_{n=1}^{N}f_{U}(n\gamma) \longrightarrow \int_{0}^{1}f_{U}(x)dx$ 。

从这两个论断，通过使用前面的逼近论据，我们可以推断出引理的证明。

对于这个引理及其推论，根据简单的动态系统，存在一个有趣的解释。在这个例子中，底层空间是由角度 θ 参数化的圆。我们也考虑一个空间到其自身的映射：在这里，我们按角度 2πγ 选取一个圆的旋转 ρ ，即，变换 $\rho :\theta \mapsto \theta + 2\pi \gamma$ 。

接下来，我们希望考虑的是，具有底层行为 ρ 的这个空间，如何随着时间演进。换句话说，我们希望考虑 ρ 的迭代，即， $\rho \hspace{0.2cm} ,\rho^{2} \hspace{0.2cm},\rho^{3 }\hspace{0.2cm},...\hspace{0.2cm},\hspace{0.2cm}\rho^{n}\hspace{0.2cm} ,$ 其中，

$\rho^{n} = \rho \ \ \circ \ \rho \ \circ \ ... \ \circ \ \rho:\theta \longmapsto \theta + 2\pi\gamma$ ，

且，在其中，我们认为行为 $\rho^{n}$ 恰好在 t = n 时刻发生。

对于圆周上的每一个Riemann可积函数 f ，我们也可以将其与旋转 ρ 的对应影响关联起来，并获得一个函数序列

$f ( \theta ) ,\: f ( \rho( \theta )),\: f ( \rho^{2} ( \theta ) ) ,\: ...\:,\:f ( \rho^{n} ( \theta ) ),...$

且 $f ( \rho^{n} (\theta ) ) = f (\theta + 2\pi n\gamma )$ 。在这个特别的背景下，则这个系统的遍历性(ergodicity)表述为,只要 γ 是非比数，对于每一个 θ，“时间平均(time average)”

$\displaystyle \lim_{N \rightarrow \infty}\frac{1}{N}\sum_{n=1}^{N}f(\rho^{n}(\theta))$

存在，并且等于“空间平均(space average)”

$\displaystyle \frac{1}{2\pi} \int_{0}^{2\pi}f(\theta)d\theta$ 。

事实上，一旦我们改变变量 $\theta = 2\pi x$ ，则这个论断不过是推论2.3的改述(rephrasing)。

回到等分布序列的问题，我们观察到，定理2.1的证明给出了下面的特征。

Weyl准则(Weyl's criterion) 对于区间[0,1)上的一个实数序列 $\xi_{1} \:, \xi_{2} \: , \:... \:,$ ,当且仅当对于所有 k ≠ 0 的整数，具有

$\displaystyle \frac{1}{N}\sum_{n=1}^{N}e^{2\pi ik\xi_{n}} \longrightarrow 0$ (当 $N \longrightarrow \infty$ 时 )，

则，这个实数序列是等分布的。这个定理的一个方向在上面得到了有效证明，相反的方向可以在练习 7 中找到。特别地，我们发现，为了理解序列 $\xi_{n}$ 的等分布属性，估算对应的“指数和(exponential sum)” $\sum_{n=1}^{N}e^{2\pi ik\xi_{n}}$ 就已足够。例如，使用Weyl准则可以证明，只要 γ 是非比数，序列 $< n^{2}\gamma>$ 是等分布的。此例及其它例子可以在练习8和9，以及问题2和3中找到。

作为最后的评述，我们提到序列 <nγ> 的分布属性的一个很好的几何解释。假设正方形的边是反射镜，并且光线从正方形内部的一点射出。光线会走出怎样的路径？

----------------------------------------------图 4. 一束光在正方形中的反射--------------------------------------

为了求解这个问题，主要思想是考虑通过连续反射初始正方形在其边上形成的平面的网格。选取一个合适的坐标轴，在正方形中由光追踪的路径对应平面上的直线 $P + ( t, \gamma t )$ 。其结果，读者可以观察到，这个路径要么将是闭合且是周期的，要么将在正方形中是稠密的。这些场景中的第一个发生的条件是，当且仅当光线(相对于正方形的一侧确定)的初始方向的斜率 γ 是比率数(rational)，而这个密度(density)可由Kronecker定理推导出。人们从等分布定理中能得出什么更有说服力的结论呢？

3. 一个连续但无处可微的函数(A continuous but nowhere differentiable function)

存在很多在某一点连续但不可微的典型函数，比如说， $f ( x ) = |x|$ 。要构造一个在任何给定的有限点集上不可微，甚至在包含可数个点的恰当集合上也是不可微的这样一个连续函数，几乎同样容易。一个更“微妙(subtle)”的问题是，是否存在一个无处可微的连续函数。在 1861年，Riemann 猜出了这个定义为

(5) $\displaystyle R(x)=\sum_{n=1}^{\infty}\frac{\sin(n^{2}x)}{n^{2}}$

的函数是无处可微的。他之所以考虑这个函数，是因为它与将在第 5 章介绍的 ζ 函数有密切联系。Riemann 从未给出证明，但在他的一次演讲中提到了这个例子。这引发了 Weierstrass 的兴趣，他在试图寻找证明时遇到了连续但无处可微函数的第一个例子。比如说，0 < b < 1 ，且 a 是一个大于 1 的整数。在 1872年，他证明了，假如 ab > 1 + 3π/2 , 则函数

$\displaystyle W(x)=\sum_{n=1}^{\infty}b^{n}\cos(a^{n}x)$

是无处可微的。

但是，如果不对Riemann原函数(original function)作最后说明(word)，这个故是不完整的。在1916年，Hardy[há:di]( 1877 年 2 月 7 日 – 1947 年 12 月 1 日，英国数学家)证明了，R 在所有 π 的非比数倍数点处不可微。然而，直到很久后的1969年，Gerver(美国数学家)才完全解决了这个问题；他首先证明，事实上，函数 R 在所有形如πp/q (p 和 q 是奇数整数)的 π 的比率数倍数点处是可微的，然后证明，R 在所有余下的情况下是不可微的。

在这一节，我们证明下面的定理。

定理3.1 假如 0 < α < 1 ,则，函数

$\displaystyle f_{\alpha}(x)=f(x)=\sum_{n=0}^{\infty}2^{-n{\alpha}}r^{i2^{n}}x$

是连续但无处可微的。

此函数的连续性是显而易见的，因为级数绝对收敛。我们所需要的 f 的关键属性在于，它具有很多消失的Fourier系数。一个跳过很多项的Fourier级数，就像以上给出的一样，或者像 W(x)一样，这样的级数被称为缺项(lacunary[ ləˈkjuːnərɪ])Fourier级数。

定理的证明实际上是求Fourier级数和的3个方法的故事。第一种就去，根据部分和公式 $S_{N}( g ) = g * D_{N}$ , 存在常规的收敛性。第二种方法，存在Cesàro可和公式 $\sigma_N( g ) = g * F_{N }$ 且 $F_{N}$ 是 Féjer 核。第三种方法，很显然与第二种有关，涉及定义为

$\displaystyle \Delta_{N}( g ) = 2\sigma_{2N}( g ) - \sigma_{N}( g )$

的延迟均值(delayed means)。

因此， $\Delta_{N}( g ) = g * [2F_{2N} - F_{N} ]$ 。这些方法用可视化最好理解，如图5所示。

----------------------------------------图 5. 3种Fourier级数的求和方法--------------------------------------

假如 $\displaystyle g(x) \sim \sum a_{n} e^{inx}$ 。则：

$\bullet$ 假如 $|n| \leq N$ ， $S_{N}$ 以项 $a_{n} e^{inx }$ 乘以 1 的形式出现；假如 $|n|> N$ ， $S_{N }$ 以项 $a_{n} e^{inx }$ 乘以 0 的形式出现。

$\bullet$ 假如 $|n| \leq N$ , $\sigma_{N}$ 以 $a_{n} e^{inx }$ 乘以 $(1-| n|/ N )$ 的形式出现；假如 $|n|> N$ , $\sigma_{N}$ 以 $a_{n} e^{inx }$ 乘以 0 的形式出现。

$\bullet$ 假如 $|n| \leq N$ , $\Delta_{N}$ 以项 $a_{n} e^{inx }$ 乘以 1 的形式出现；假如 $N \leq |n| \leq 2N$ ， $\Delta_{N}$ 以项 $a_{n} e^{inx }$ 乘以 $2[1-|n|/(2N)]$ 的形式出现；假如 $|n|> 2N$ , $\Delta_{N}$ 以项 $a_{n} e^{inx }$ 乘以 0 的形式出现。

例如，注意

$\displaystyle \begin{array}{rl} \sigma_{N}(g)(x)&=\displaystyle \frac{s_{0}(g)(x)+s_{1}(g)(x)+...+s_{N-1}(g)(x)}{N} \\ &=\displaystyle \frac{1}{N}\sum_{\ell=0}^{N-1}\sum_{|k \leq \ell|}^{}a_{k}e^{ikx} \\ &=\displaystyle \frac{1}{N}\sum_{|n| \leq N}^{}(N-|n|)a_{n}e^{inx} \\ &=\displaystyle \frac{1}{N}\sum_{|n| \leq N}^{}(1-\frac{|n|}{N})a_{n}e^{inx} \end{array}$ 。

其它诊断的证明与此相似。

延迟均值有两个重要的特征。在一方面，它们的属性与Cesàro均值的(好)特征紧密相关。在另一方面，对于那些像 f 一样具有缺项属性的级数而言，延迟均值在本质上等于部分和。特别地，注意，对于我们的函数 $f=f_{\alpha}$

(6) $\displaystyle S_{N}(f)=\Delta N^{'}(f)$ ,

其中， $N^{'}$ 是形如 $2^{k}$ 且 $N^{'} \leq N$ 的最大整数，通过考察图5 及 f 的定义，可以看出这是显而易见的。

我们回到严格意义上的定理证明，并采用反证法论证；即，我们假设 f 在某个 $x_{0}$ 点存在导数 $f^{'}(x_{0})$ 。

引理 3.2 令 g 为在 $x_{0}$ 点可微的任意连续函数。则 Cesàro均值满足 $\sigma_N^{'}( g ) = O( \log N )$ , 因此, $\Delta_N( g )^{'}( x_0 ) = O( \log N )$ 。(译注：第2章提到过，这种 “O” 记法表示左侧以右侧的常数倍为界。)

证明：

首先，我们有

$\displaystyle \Delta_N( g )^{'}( x_0 ) = \int_{-\pi}^{\pi}F^{'}_{N}(x_{0}-t)g(t)dt=\int_{-\pi}^{\pi}F^{'}_{N}(t)g(x_{0}-t)dt$ ，

其中， $F_{N}$ 是 Fejér 核。因为 $F_{N}$ 是周期的，我们有 $\displaystyle \int_{-\pi}^{\pi}F^{'}_{N}(t)dt=0$ 且意味着

$\displaystyle \Delta_N( g )^{'}( x_0 ) = \int_{-\pi}^{\pi}F^{'}_{N}(t) \left | g(x_{0}-t)-g(x_{0}) \right | dt$ 。

从假设 g 在 $x_{0}$ 点可微我们得到

$\displaystyle \left | \Delta_N( g )^{'}( x_0 ) \right | \leq C\int_{-\pi}^{\pi}\left |F^{'}_{N}(t)\right | \left |t \right |dt$ 。

现在，观穿到 $F^{'}_{N}$ 满足两个估算

$\left | F^{'}_{N}(t) \right | \leq AN^{2}$ 和 $\displaystyle \left | F^{'}_{N}(t) \right | \leq \frac{A}{t^{2}}$ 。

对于第一个不等式，我们记得， $F_{N}$ 是一个次数为 N 的三角多项式，其系数以 1 为界。因此， $F^{'}_{N}$ 是一个次数为 N 的三角多项式，其系数不大于 N 。因此 $|F ^{'}(t)| \leq (2N + 1) N \leq AN^{2}$ 。

对于第二个不等式，我们记得

$\displaystyle F_{N}(t)=\frac{1}{N}\frac{\sin^{2}(Nt/2)}{\sin^{2}(t/2)}$ 。

微分这个表达式，我们得到两项：

$\displaystyle \frac{\sin(Nt/2)\cos(Nt/2)}{\sin^{2}(t/2)}-\frac{1}{N}\frac{\cos(t/2)\sin^{2}(Nt/2)}{\sin^{3}(t/2)}$ 。

然后，假如我们使用两个事实， $|\sin(Nt/2)| \leq CN|t|$ 和 $|\sin(t/2)| \geq C|t|$ (对于| t | ≤ π) ,我们得到对 $F^{'}_{N}$ 的预期估算。使用这些估计，我们求得

$\displaystyle \begin{array}{rl} \left | \sigma_{N}(g)^{'}(x_{0}) \right | & \displaystyle \leq C \int_{|t| \geq (\frac{1}{N})} \left | F^{'}_{N}(t) \right | \left | t \right |dt + C \int_{|t| \leq (\frac{1}{N})} \left | F^{'}_{N}(t) \right | \left | t \right |dt \\ &\displaystyle \leq CA \int_{|t| \geq (\frac{1}{N})} \left | F^{'}_{N}(t) \right | \frac{dt}{|t|} dt +CAN \int_{|t| \leq (\frac{1}{N})}dt \\ & =O( \log N ) + O( 1 ) \\ & =O( \log N ) \end{array}$ 。

一旦我们调用 $\Delta_{N}(g)$ 的定义，就完成了对这个引理的证明。

引理 3.3 假如 $2N = 2^{n}$ , 则

$\displaystyle \Delta_{2N}( f ) - \Delta_{N}( f ) = 2^{-n\alpha} e^{i2^{n} x}$ 。

这个引理从前面的观察(6)可以推出，因为 $\Delta_{2N}( f ) = S_{2N}( f )$ 和 $\Delta_{N}( f ) = S_{N}( f )$ 。

现在，按第一个引理，我们有

$\Delta_{2N}^{'}( f )( x_{0} ) - \Delta_{N}^{'}( f )( x_{0} ) = O(\log N )$ ,

且第二个引理也意味着

$\displaystyle \left | \Delta_{2N}^{'}( f )( x_{0} ) - \Delta_{N}^{'}( f )( x_{0} ) = O(\log N ) \right | =2^{n(1-\alpha)} \geq cN^{(1-\alpha)}$ 。

这与预期相悖，因为 $N^{(1-\alpha)}$ 比 $\log N$ 增长得更快。

关于我们的这个函数 $\displaystyle f_{\alpha}(x)=\sum_{n=0}^{\infty}2^{-n\alpha}e^{i2^{n}x}$ ，按顺序另加几条评述。

相对于上面的函数 R 和 W，这个函数是复数值的，因此， $f_{\alpha}(x)$ 无处可微并不意味着其实数部分和虚数部也同样无处可微。然而，通过少许修改我们的证明便可证明，事实上， $f_{\alpha}(x)$ 的实数部分

$\displaystyle \sum_{n=0}^{\infty}2^{-n\alpha}\cos(2^{n}x)$ ,

以及其虚数部分，两者都是无处可微的。为了理解这一点，首先通过第一个证明观察到，引理3.2具有下列泛化性：假如 g 是一个在 $x_{0}$ 点可微的连续函数，则

$\Delta_N( g )^{'}( x_{0} + h ) = O( \log N )$ (只要 $|h| \leq c/ N$ ) 。

则，我们继续以 $\displaystyle F(x)= \sum_{n=0}^{\infty}2^{-n\alpha}\cos(2^{n}x)$ 推进，如上，注意到， $\Delta_{2N}( F ) - \Delta_{N}( F )=2^{-n \alpha}\cos(2^{n}x)$ ；其结果就是，假设 F 在 $x_{0}$ 点可微，则当 $2N = 2^{n}$ 且 $|h| \leq c/ N$ 时，我们得到

$\displaystyle \left | 2^{n(1-\alpha)}\sin \left [2^{n} (x_{0}+h) \right ] \right | = O( \log N )$ 。

为了得出矛盾的逻辑，我们仅需选取 h 使得其满足 $\displaystyle \sin \left [2^{n} (x_{0}+h) \right ]=1$ 即可；通过设置 δ 使其等于从 $2^{n}x_{0}$ 到形如 $(k + 1/2)\pi(k \in \mathbb{Z})$ 的最近的数的距离(因此， $\delta \leq \pi/2$ ) ，并且取 $h = ±\delta/2^{n}$ ，这样即可完成证明。

显然，当 α > 1 时，函数 $f_{\alpha}$ 是连续可微的，因为级数可以逐项微分。最后，我们已经证明了当 α < 1 时函数无处可微，事实上这可以推广到 α = 1的情况，只需通过论据的合适改进即可(见第5章问题8)。事实上，使用这些更详尽的方法，读者也可以证明，对于 Weierstrass 函数，假如 ab ≥ 1 ，则其是无处可微的。

4. 圆周上的热传导方程(The heat equation on the circle)

作为最后的例释(illustration),我们回到最初由Fourier考虑的热传导(diffusion)问题。

假如给我们一个环上位于 t = 0 时刻的初始温度分布，并要求我们描述环上 t > 0 的某时刻的温度。

这个环是一个单位圆的模型。圆上的一点用其角度 θ = 2πx 描述，其中变量 x 位于0 到 1 之间。假如用 u(x,t ) 表示用角度 θ 描述的一点在 t 时刻的温度，则类似第 1 章中给出来的考量结果，u 满足微分方程

(7) $\displaystyle \frac{ \partial u}{\partial t}=c\frac{\partial^{2}u}{\partial x^{2}}$ 。

常量 c 是一个正的物理常量，其取决于制造环的材料(参见第1章第2.1节)。在重新调节时间变量 t 之后，我们可以假设 c = 1 ，假如 f 是我们的初始数据，我们施加一个已知条件

$u(x,0) = f ( x )$ 。

为了解这个问题，我们分离变量并寻找形如

$u(x,t) = A(x)B(t)$

的特解。

然后，则 u 的表达式插入热传导方程，我们得到

$\displaystyle \frac{B^{'}(t)}{B(t)}=\frac{A^{''}(x)}{A(x)}$ 。

因此，等式两侧都是常量，比如说，设其等于 λ 。因为 A 一定是周期为 1 的周期函数，我们发现，唯一的可能性是 $\lambda = -4\pi^{2} n^{2}$ , 其中，n ∈ ℤ 。则 A 是指数函数 $e^{2\pi inx}$ 和 $e^{-2\pi inx}$ 的线性组合，而 B ( t )是函数 $e^{-4\pi^{2} n^{2} t}$ 的倍数。通过叠加这些解，导出方程

(8) $\displaystyle u(x,t)=\sum_{n=-\infty}^{\infty}a_{n}e^{-4\pi ^{2}n^{2}t}e^{2\pi inx}$ ，

其中，设置 t = 0 , 我们发现 $\{ a_{n} \}$ 是 f 的 Fourier系数。

注意，当 f 是 Riemann可积的时候，系数 $a_{n}$ 是有界的。因为因子 $e^{-4\pi ^{2}n^{2}t}$ 以极快的速度趋近于 0 , 其定义的 u 这个级数收敛。事实上，在这种情况下，u 是二次可微的，且作为方程 (7) 的解。

针对边界条件，很自然地出现的问题如下：当 t ⟶ 0 的时候，u(x,t) ⟶ f ( x ) ？如果是，又是在什么意义上？简单地应用Parseval恒等式证明，在均值平方的意义上，这个极限成立(练习11)。为了更好地理解方程解(8)的属性，我们将其写为

$u(x,t) = ( f * H_{t })( x )$ ，

其中， $H_{t }$ 圆的热传导核(heat kernel for the circle),由

(8) $\displaystyle H_{t}=\sum_{n=-\infty}^{\infty}e^{-4\pi ^{2}n^{2}t}e^{2\pi inx}$

给出，其中，周期为 1 的函数的卷积定义为

$\displaystyle ( f * g )( x ) =\int_{0}^{1}f(x-y)g(y)dy$ 。

热传导核和(第2章中给出的)Poisson核之间的类比在练习12中给出。然而，与Poisson核的情况不同，热传导核不存在基本公式。因此，证明它是一个好核(在第2章好核的意义上)。证明并不明显，需要使用著名的Poisson求和公式，这将在第 5 章中介绍。作为一个推论，我们也将会发现， $H_{t }$ 处处为正，从其定义表达式(9)来看，这也是一个不明显的事实。假如我们以处处小于 0 初始温度分布 f 开始。则对于所有的 t ，预期 u(x,t ) ≤ 0 在物理上是合理的，因为热量由热向冷传导(travels)。现在，

$\displaystyle u(x,t) = \int_{0}^{1}f(x-y)H_{t} (y)dy$ 。