参考内容:
图论——并查集(详细版)
并查集(Disjoint-set)是一种精巧的树形数据结构,它主要用于处理一些不相交集合的合并及查询问题。一些常见用途,比如求联通子图、求最小生成树的 Kruskal 算法和求最近公共祖先(LCA)等。
并查集的理念是只关注个体属于哪个阵营,并不关心这个阵营中个体内部的关系,比如我们常说的张三是李家沟的,王二是王家坝的。同时并查集借助个体代表集体的思想,用一个元素代表整个群体,就像我们开学都会有学生代表、教师代表讲话一样,在台上讲话的那一个学生就代表了学校所有的学生。
并查集基本操作
并查集的基本操作主要有初始化 init、查询 find和合并 union操作。
初始化
在使用并查集的时候,常常使用一个数组fa来存储每个元素的父节点,在一开始的时候所有元素与其它元素都没有任何关系,即大家相互之间还不认识,所以我们把每个元素的父节点设为自己。
#define ARR_LEN 6000int fa[ARR_LEN];void init(int n)
{for(int i = 1; i <= n; i++)fa[i] = i;
}
查询
查询即找到指定元素的祖先。需要注意的是,这里我们需要找到指定元素的根祖先,不能找到爸爸或者爷爷就停止了,而是要找到查找不下去了为止,所以要不断的去递归下去,直到找到父亲为自己的结点才结束。
int find(int i)
{if(i == fa[i]) // 递归出口return i;elsereturn find(fa[i]); // 不断向上查找祖先
}
考虑下面的场景,假如第一次我们需要查询元素5的祖先,第二次需要查询元素4的祖先,会发现第一次查询包含了第二次查询的计算过程,但我们的程序却傻傻的计算了两次,有没有办法去来优化查询过程,让每一次查询都能利用到此前查询计算的便利?

考虑到并查集并不关心某个元素的爸爸、爷爷是谁,只关心最终的祖先是谁,所以我们可以在查询的过程中顺便做一些修改,比如在查询5的过程中,顺便就把4和2的父亲给修改为1,即我们在查找过程中进行路经压缩
int find(int i)
{if(i == fa[i]){return i;} else {fa[i] = find(fa[i]); // 进行路径压缩return fa[i];}
}
合并
合并操作即介绍两个人相互认识,将他们纳入同一个帮派,只需要将俩元素的父亲修改为同一个即可。
void union(int i, int j)
{int fa_i = find(i);int fa_j = find(j);fa[fa_i] = fa_j;
}
相关练习题目
洛谷 P1551 亲戚
题目连接:https://www.luogu.com.cn/problem/P1551
题目描述
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
规定: x x x 和 y y y 是亲戚, y y y 和 z z z 是亲戚,那么 x x x 和 z z z 也是亲戚。如果 x , y x,y x,y 是亲戚,那么 x x x 的亲戚都是 y y y 的亲戚, y y y 的亲戚也都是 x x x 的亲戚。
输入格式
第一行:三个整数 n , m , p , ( n , m , p ≤ 5000 ) n,m,p,(n,m,p≤5000) n,m,p,(n,m,p≤5000) 分别表示有 n n n 个人, m m m 个亲戚关系,询问 p p p 对亲戚关系。
以下 m m m 行:每行两个数 M i , M j , 1 ≤ M i , M j ≤ n M_i,M_j,1≤M_i,M_j≤n Mi,Mj,1≤Mi,Mj≤n,表示 M i M_i Mi 和 M j M_j Mj 具有亲戚关系。
接下来 p p p 行:每行两个数 P i , P j P_i,P_j Pi,Pj,询问 P i P_i Pi 和 P j P_j Pj 是否具有亲戚关系。
输出格式
p p p 行,每行一个Yes或No。表示第 i i i 个询问的答案为“具有”或“不具有”亲戚关系。
输入输出样例
# 输入
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6# 输出
Yes
Yes
No
题目解析
可以发现这是一个非常标准的并查集问题,简直和并查集模版如出一辙,因此直接将所有关系读取后进行合并,然后直接查询父亲是否为同一个即可。
#include<bits/stdc++.h>
using namespace std;#define ARR_LEN 6000int fa[ARR_LEN];void init(int n)
{for(int i = 1; i <= n; i++)fa[i] = i;
}int find(int i)
{if(i == fa[i]){return i;} else {fa[i] = find(fa[i]);return fa[i];}
}void union(int i, int j)
{int fa_i = find(i);int fa_j = find(j);fa[fa_i] = fa_j;
}int main()
{int n, m, p;int a, b;cin>> n >> m >> p;init(n);for(int i = 0; i < m; i++){cin >> a >> b;union(a, b);}for(int i = 0; i < p; i++){cin >> a >> b;int fa_a = find(a);int fa_b = find(b);if(fa_a == fa_b)cout<<"Yes"<<endl;elsecout<<"No"<<endl;}
}
杭电 OJ1213 How Many Tables
题目连接:https://acm.hdu.edu.cn/showproblem.php?pid=1213
题目描述
Today is Ignatius’ birthday. He invites a lot of friends. Now it’s dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.
One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.
For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.
输入格式
The input starts with an integer T ( 1 < = T < = 25 ) T(1<=T<=25) T(1<=T<=25) which indicate the number of test cases. Then T T T test cases follow. Each test case starts with two integers N N N and M ( 1 < = N , M < = 1000 ) M(1<=N,M<=1000) M(1<=N,M<=1000). N N N indicates the number of friends, the friends are marked from 1 1 1 to N N N. Then M M M lines follow. Each line consists of two integers A A A and B ( A ! = B ) B(A!=B) B(A!=B), that means friend A A A and friend B B B know each other. There will be a blank line between two cases.
输出格式
For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.
输入输出样例
# 输入
2
5 3
1 2
2 3
4 55 1
2 5# 输出
2
4
题目解析
分析可以发现,这个问题要我们做的是统计在所有元素合并之后,统计总共有多个和集合。很轻松就能写出下面的 AC 代码。类似的问题还有杭电 OJ1232 畅通工程。
读者大人可以在此基础上继续进行延伸,我们实际生活中每个桌子只能坐 8 个人,假设还需要考虑每桌人数的容量,又如何进行改进呢?
#include<bits/stdc++.h>
using namespace std;#define ARR_LEN 6000int fa[ARR_LEN];void init(int n)
{for(int i = 1; i <= n; i++)fa[i] = i;
}int find(int i)
{if(i == fa[i]){return i;} else {fa[i] = find(fa[i]);return fa[i];}
}void union(int i, int j)
{int fa_i = find(i);int fa_j = find(j);fa[fa_i] = fa_j;
}int main()
{int n, m, a, b, t;cin>>t;for(int i = 0; i < t; i++){cin>>n>>m;int ans = 0;init(n);for(int i = 0; i < m; i++) {cin>>a>>b;union(a, b);}for(int i = 1; i <= n; i++) {// 如果父亲是自己,那么就表示一个独立的集合if(find(i) == i)ans++;}cout<<ans<<endl;}}
杭电 OJ1272 小希的迷宫
题目连接:https://acm.hdu.edu.cn/showproblem.php?pid=1272
题目描述
小希设计了一个迷宫让 Gardon 玩,首先她认为所有的通道都应该是双向连通的,就是说如果有一个通道连通了房间 A 和 B,那么既可以通过它从房间 A 走到房间 B,也可以通过它从房间 B 走到房间 A,为了提高难度,小希希望任意两个房间有且仅有一条路径可以相通(除非走了回头路)。小希现在把她的设计图给你,让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子,前两个是符合条件的,但是最后一个却有两种方法从 5 到达 8。
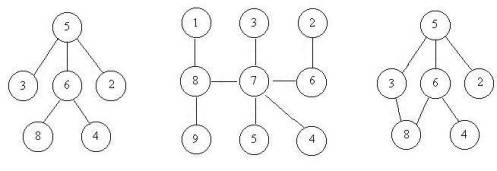
输入格式
输入包含多组数据,每组数据是一个以 0 0 结尾的整数对列表,表示了一条通道连接的两个房间的编号。房间的编号至少为 1,且不超过 100000。每两组数据之间有一个空行。整个文件以两个 -1 结尾。
输出格式
对于输入的每一组数据,输出仅包括一行。如果该迷宫符合小希的思路,那么输出Yes,否则输出No。
输入输出样例
# 输入
6 8 5 3 5 2 6 4
5 6 0 08 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 03 8 6 8 6 4
5 3 5 6 5 2 0 0-1 -1# 输出
Yes
Yes
No
题目解析
其实这个问题就是让我们判断一个连通图中是否存在环,那么问题就转换为寻找出现环的条件。其实不难发现出现下面两种情况时,连通图即存在环。
- 在查找过程中,发现两个不同元素的父亲是相同的;
- 若不存在环,则边的数量一定比顶点数量少 1。
#include<bits/stdc++.h>
using namespace std;#define ARR_LEN 100010int fa[ARR_LEN];
bool visited[ARR_LEN]; // 用于辅助记录顶点的数量
int edges, points; // 记录顶点和边的数量
bool hascycle; // 是否存在环void init()
{hascycle = false;edges = 0;points = 0;for(int i = 1; i < ARR_LEN; i++)fa[i] = i, visited[i] = false;
}int find(int i)
{if(i == fa[i]){return i;} else {fa[i] = find(fa[i]);return fa[i];}
}void union(int i, int j)
{int fa_i = find(i);int fa_j = find(j);// 两个元素祖先相同,存在环if(fa_i == fa_j) {hascycle = true;} else {visited[i] = true;visited[j] = true;edges++;fa[fa_i] = fa_j;}
}int main()
{int a, b;init();while(cin>>a>>b) {if(a == 0 && b == 0) {cout<<"Yes"<<endl;continue;}if(a == -1 && b == -1) {return 0;}union(a, b);while(cin>>a>>b){if(a == 0 && b == 0) {break;}union(a, b);}if(hascycle) {cout<<"No"<<endl;continue;}for(int i = 1; i < ARR_LEN; i++){if(visited[i]) {points++;}}if(points == edges + 1) {cout<<"Yes"<<endl;} else {cout<<"No"<<endl;}init();}
}