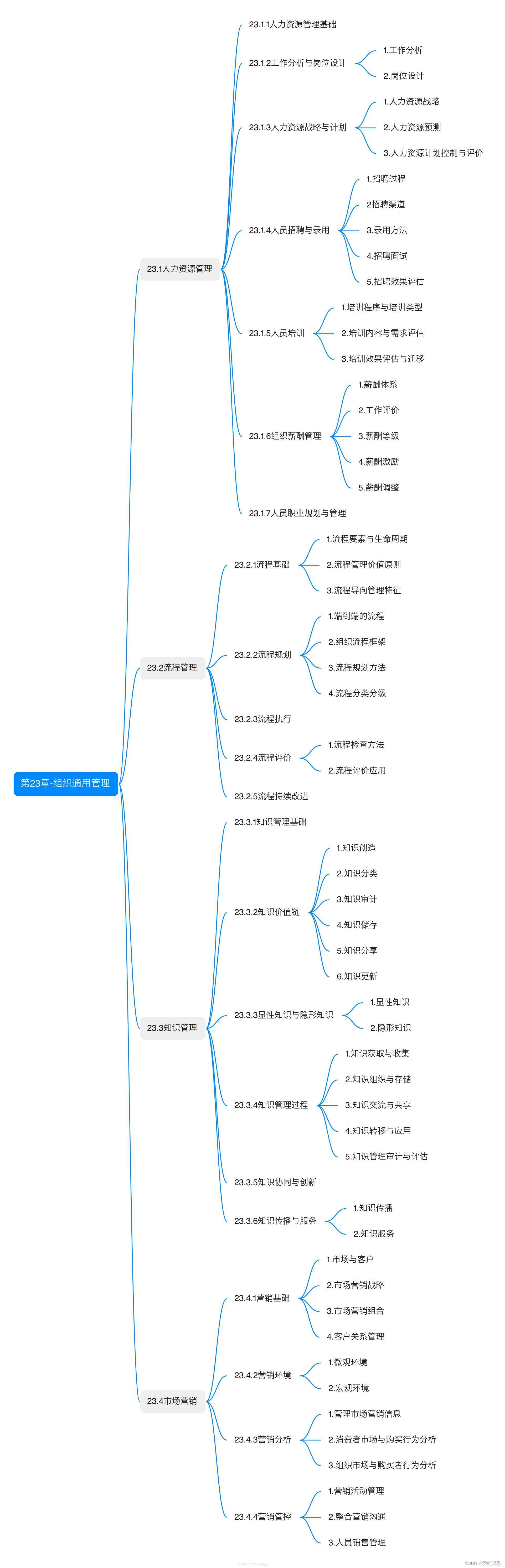
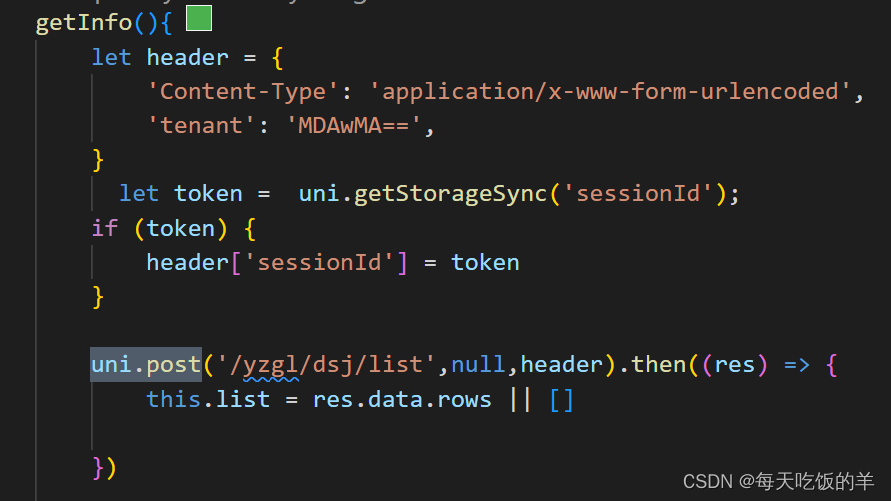
认识填充 (padding)
随着卷积层数的加深,输出进一步缩小,那么最终会导致输出很快就只剩下1∗1的数组,这也就没办法继续计算了,所以提出了填充的方法来方便网络的进一步加深。 其实填充的原因有两点:
- 不填充会导致图像逐渐变小,使网络深度无法达到很深;
- 不填充会导致边缘和角落的像素学习不充分,被覆盖的次数不多。

第二点的意思是指例如上图中的例子,输入数组的四个顶点:1,3,7,9在进行的四次卷积运算中,只被计算了一次,所以卷积学习的不充分,填充就是让卷积网络能够将边缘的角落也能多次学习,从而更全面地发现特征。
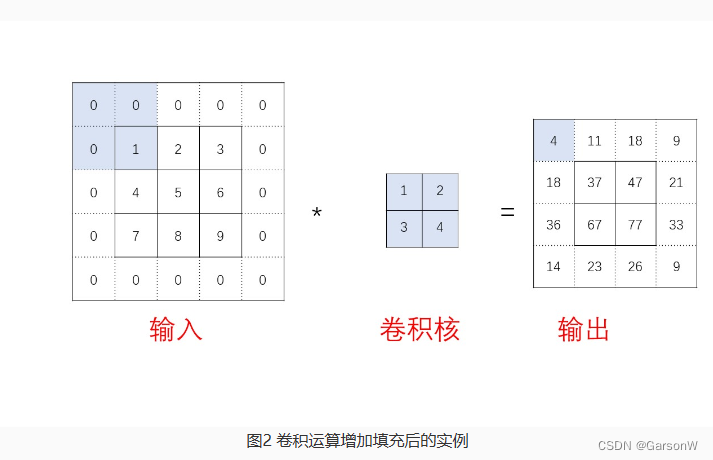
填充的方法就是在输入的高和宽两侧分别填充了0元素,再进行卷积运算。
如何计算填充
这里需要介绍两种卷积核
- Valid 卷积,表示的是不进行填充的卷积核;
- Same 卷积,表示填充之后,进行运算之后的形状不变。
假设输入的形状为n∗n,填充的大小为p,卷积核的形状为f∗f,当使用的是 Same 卷积时,输出的形状也是n∗n。
计算的等式为:n+2p−f+1=n,解得p=2f−1。
从结果中也可以看出,当卷积核的高宽为偶数时,就容易造成p的结果不是一个整数,这也就是上一张中提到卷积核通常高和宽均为奇数的其中一个原因。
如何调用Pytorch中的填充
nn.Conv2d()中的参数padding就是来控制填充大小的。padding=0表示四周不进行零填充,而padding=1则表示四周进行1个像素点的零填充,当然,也可以用padding=(2,1)来表示在高和宽两侧的填充数分别为2和1。