**

描述

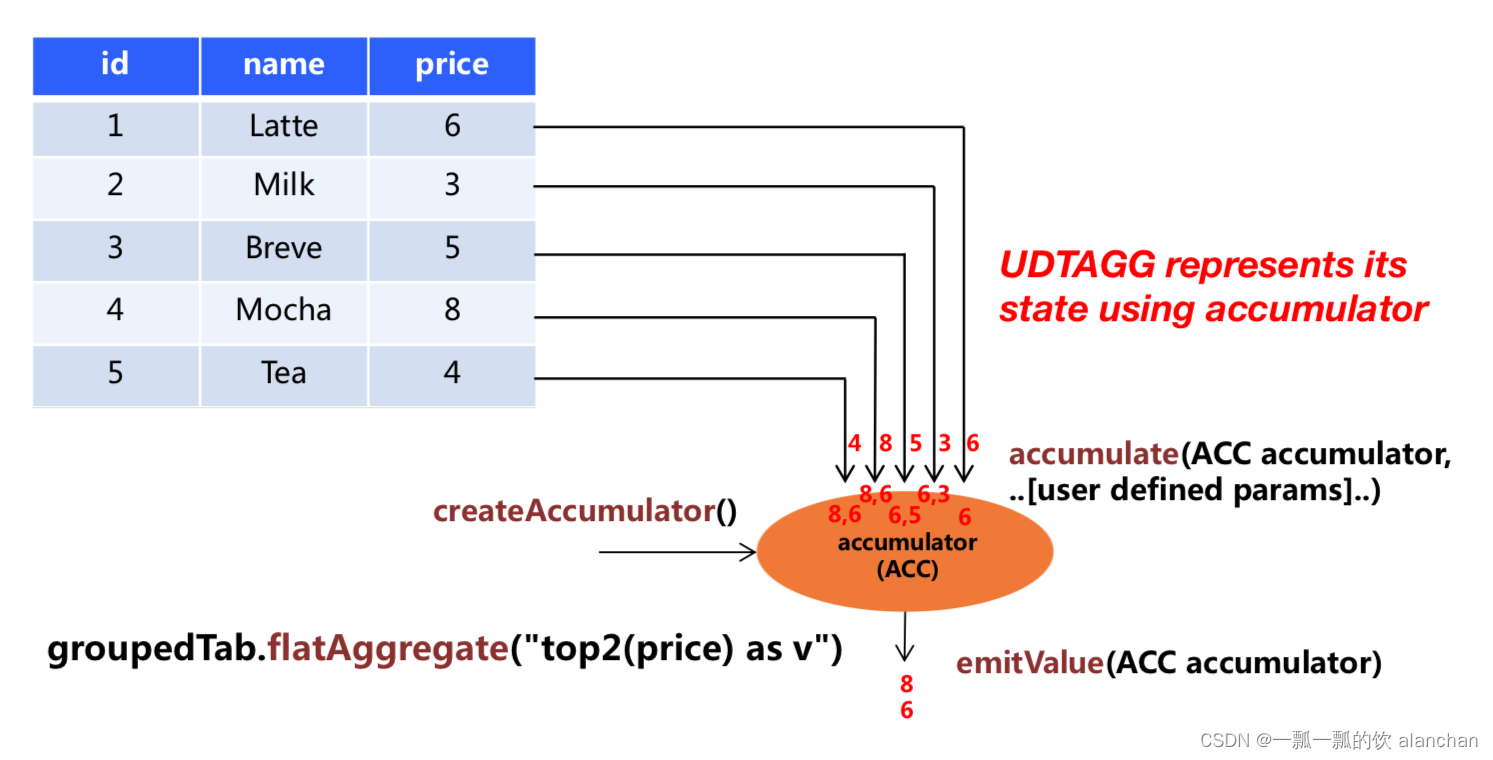
给定一个数组 A[0,1,…,n-1] ,请构建一个数组 B[0,1,…,n-1] ,其中 B 的元素 B[i]=A[0]A[1]…*A[i-1]A[i+1]…*A[n-1]（除 A[i] 以外的全部元素的的乘积）。程序中不能使用除法。（注意：规定 B[0] = A[1] * A[2] * … * A[n-1]，B[n-1] = A[0] * A[1] * … * A[n-2]）
对于 A 长度为 1 的情况，B 无意义，故而无法构建，用例中不包括这种情况。

数据范围：1≤n≤10 ，数组中元素满足 ∣val∣≤10
示例1
输入：
[1,2,3,4,5]
返回值：
[120,60,40,30,24]
示例2
输入：
[100,50]
复制
返回值：
[50,100]

题目分析

这题算个easy的题,原因是它的暴力解法很简单。如果要求时间复杂度是o(n),我觉得可以算作一个mediem题。题目描述的很清晰，没什么弯弯绕绕，就是要我们输出一个给定数组乘积的数组，数组的每一项都分别少乘一个数。

题解

暴力解法

暴力解法很简单，直接根据题意，每次乘的时候少乘一个数，2次for循环就能解决问题，下面直接上代码。

import java.util.*;
public class Solution {public int[] multiply (int[] A) {int[] b= new int[A.length];for(int i=0;i<A.length;i++){int res = 1;for(int j=0;j<A.length;j++){if(i==j) continue;res = res*A[j];}b[i] = res;}return b;}
}

暴力解法不做过度解释，相信大家都能看懂，同时它的时间复杂度也达到了惊人的o(n²)

两次遍历

为了降低暴力解法的时间复杂度，我们必须得有利用空间来置换时间的想法。我们可以把数组B的结果用一个表格来列举出来，如下图：

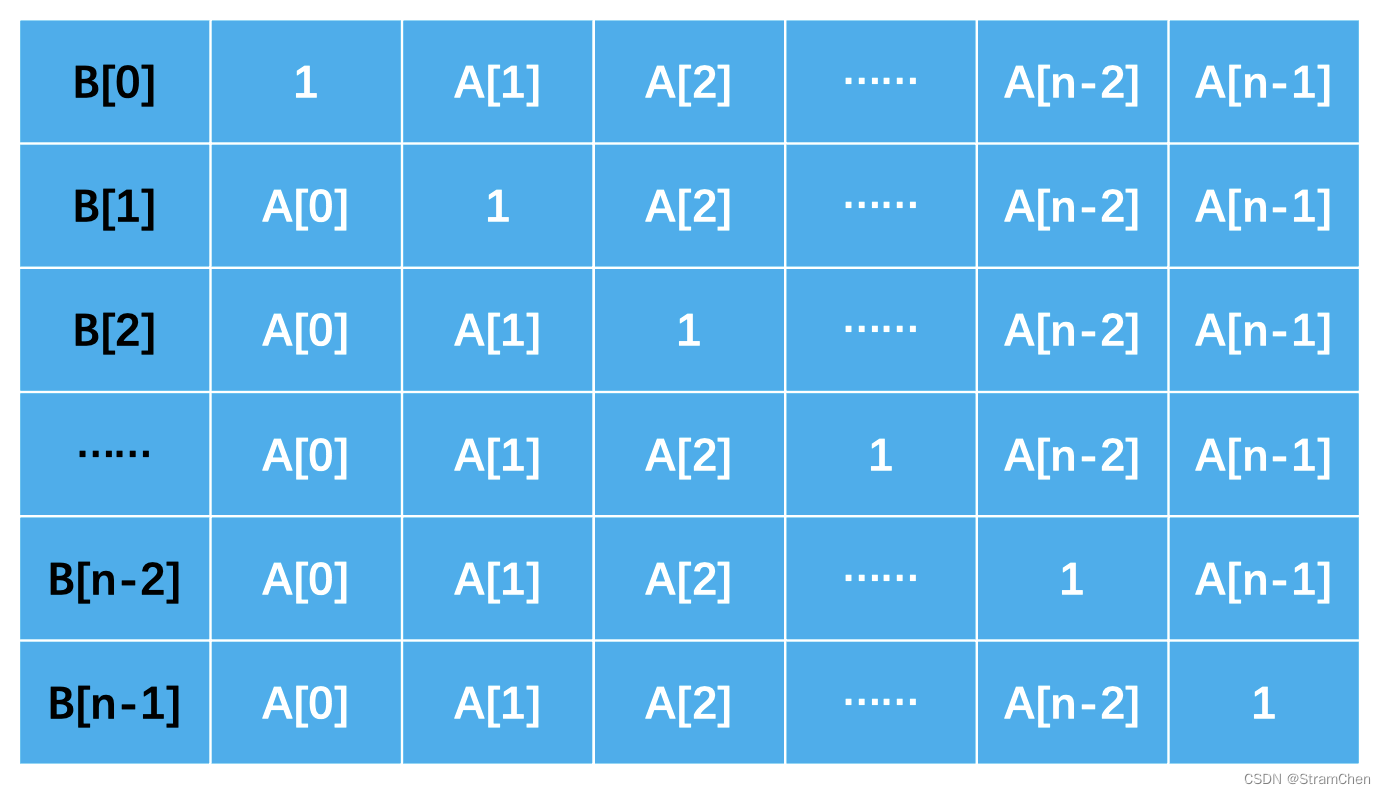
我们可以先忽略掉B[n]这一行，直接看带有A的举证

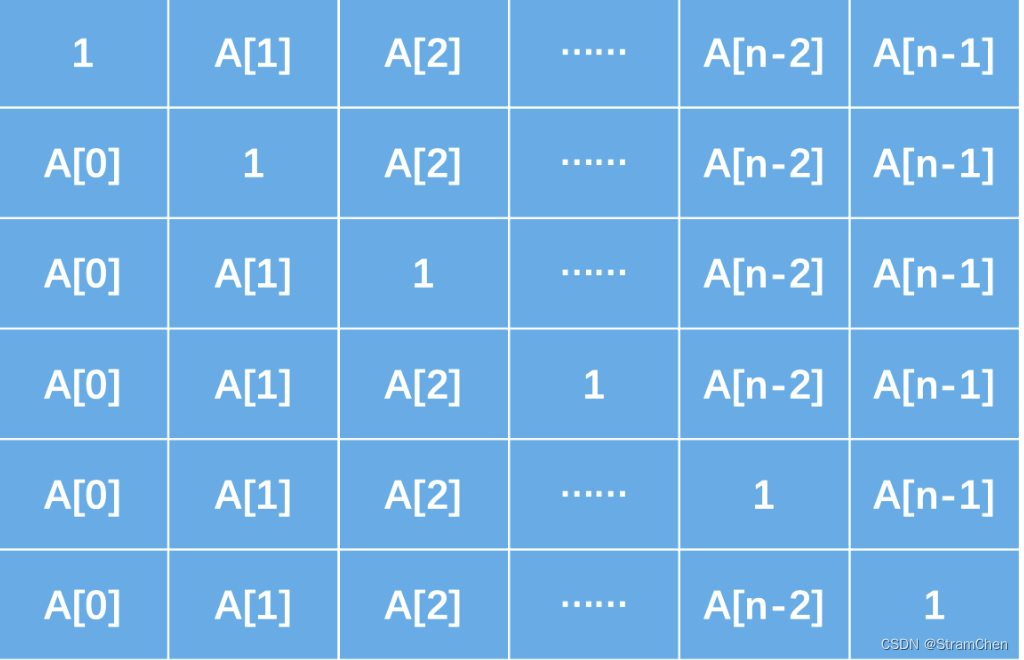
我们可以看到，这个矩阵以1为分割线，将矩阵分为了上下两个三角形。而B的结果就是这个矩阵每一行的乘积。
下三角用连乘可以很容求得，上三角，从下向上其实也是连乘。

因此我们的思路就很清晰了，先算下三角中的连乘，即我们先算出B[n]中的一部分，然后倒过来按上三角中的分布规律，把另一部分也乘进去，两次遍历，结果就出来了。

接下来我们直接上代码:

import java.util.*;
public class Solution {public int[] multiply (int[] A) {int[] b= new int[A.length];b[0] = 1;//第一次遍历算上三角，也就是对角线下面的三角形，我们根据规律可以看出b[0]的值直//接就是1，后面b[i]的值就是上一层b[i-1]的值乘上A[i-1]即可。for(int i=1;i<A.length;i++){b[i] = A[i-1]*b[i-1];}//第二次遍历，我们再把下三角累乘出来，分别跟上面的b[i]做乘积，这样每层的结果就//出来了，同时我们需要一个temp临时变量来记录每次累乘的结果int temp = 1;for(int i=A.length-1;i>=0;i--){//每次累乘的结果乘上b[i]就是那一行的值咯b[i] = b[i]*temp;/再进行下一次累乘temp = temp*A[i];  }return b;}
}

动态规划

说到动态规划，我们肯定会想到动态规划的三个步骤
1.确定状态
2.定义状态转移方程
3.求得最优解

其实上面两次遍历的思想我们稍微进行转变一下，就可以变成动态规划了，我们把第一次为了计算上三角而遍历累乘的结果利用动态规划数组进行存储起来，然后再反向对动态规划数组的结果和下三角逐行相乘即可得到结果数组。

1.确定状态

我们利用动态规划主要是为了保存上三角的值，那么dp[0]=1;

2.定义状态转移方程

状态转移方程肯定就是三角下一行的值等于上一行的值乘以A数组上一行对应下标的值，也就是dp数组第i行的值等dp数组第i-1行的值乘上A数组第i-1的下标的值。
转换成代码形式就是
dp[i] = dp[i-1]*A[i-1]

3.求得最优解

得到上三角的值，我们再反向对动态规划数组的结果和下三角逐行相乘即可得到结果数组。
其实我们只需要将两次遍历的代码中B数组用dp数组代替就可以了，代码其实可以是一摸一样的，是不是很容易。