红黑树
- 红黑树的特点
- 红黑树的模拟实现
- 红黑树的底层结构
- insert的实现
- 实现思路
- 更新黑红比例的逻辑
- insert的完整代码
- insert的验证
- 源码
红黑树的特点
-
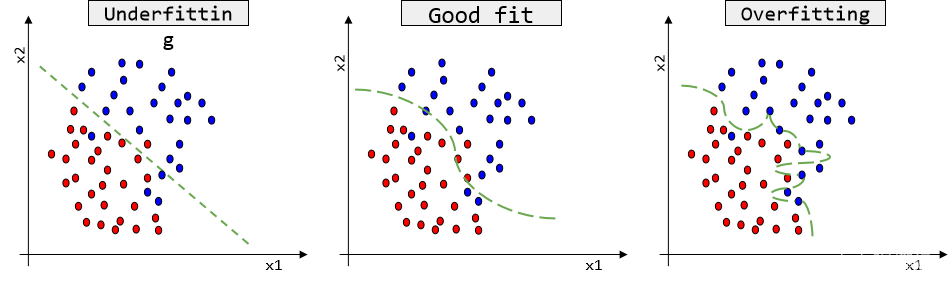
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是
Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的. -
红黑树的特点:
- 节点颜色不是红色就是黑色
- 根节点是黑色的
- 每一条路径的黑色节点数目是相同的, (注意:
这里的路径是从根节点到NIL(黑色)节点) - 每一条路径不允许出现连续的红色节点
-
路径是从根节点 到 NIL节点的

🗨️满足上面的条件, 为啥就能保证 红黑树确保没有一条路径会比其他路径长出俩倍呢?
- 根据上述的特点, 我们可以得知:
当每条路径的黑色节点数目一定的情况下, 最短路径是全黑, 最长路径是黑红相间的
如果我们保证最长路径 不超过 最短路径的二倍就可以了

红黑树的模拟实现
红黑树的底层结构
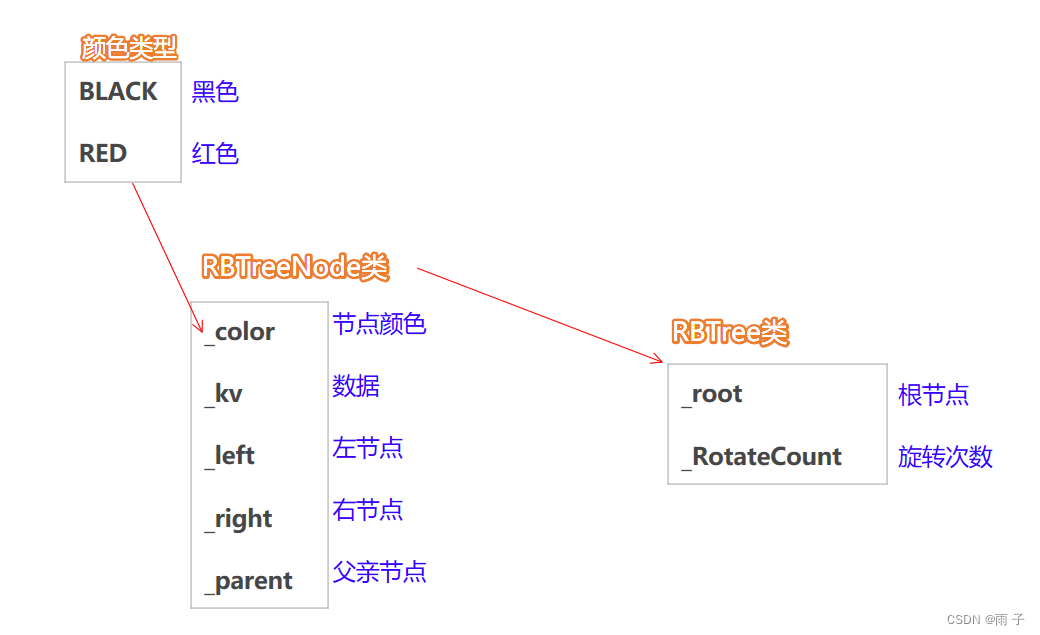
- 颜色类型
// 枚举
enum Color
{RED,BLACK
};
- RBTreeNode类
template<class K, class V>
struct RBTreeNode
{
public:RBTreeNode(const pair<K, V> kv):_kv(kv){}public:pair<K, V> _kv;Color _color = BLACK;RBTreeNode<K, V>* _left = nullptr;RBTreeNode<K, V>* _right = nullptr;RBTreeNode<K, V>* _parent = nullptr;
};
- RBTree类
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;public:RBTree(){}private:// 根节点Node* _root = nullptr;// 记录旋转次数int RotateCount = 0;
}
insert的实现
实现思路
二叉搜索树的插入逻辑 + 更新黑红比例
bool Insert(const pair<K, V> kv)
{if (_root == nullptr){// 根节点是黑色的_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = _root;Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 新建一个节点, 默认是红色cur = new Node(kv);cur->_color = RED;// 链接cur 和 parentif (cur->_kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 更改黑红比例// ...// ...// 更新完黑红比例后, 就返回truereturn true;
}
🗨️ 不能出现连续的红色节点 ⇒ 我们插入节点给个黑色节点多好, 为啥还要给红色节点冒风险呢?
因为, 我们插入的节点颜色是 红色, 插入的位置就有两种可能:
- 插入到黑色节点的后面 — — 正常的情况, 不需要进行更新
- 插入到红色节点的后面 — — 出现连续的红色节点, 需要
更新这一条支路 (当前节点到祖宗节点这一条路径)中的黑红比例
更新黑红比例的逻辑
由于 插入前, 是符合红黑树的性质,
插入的节点是红色 ⇒ 插入后才会出现连续的红色节点
⇒ 设插入的新节点为 cur(红色) ,
则父亲节点 paren 为 红色, 祖父节点 grandfather 为 黑色 ⇒ 这才符合 插入前符合红黑树的特点, 插入后才会出现连续的红色节点的情况
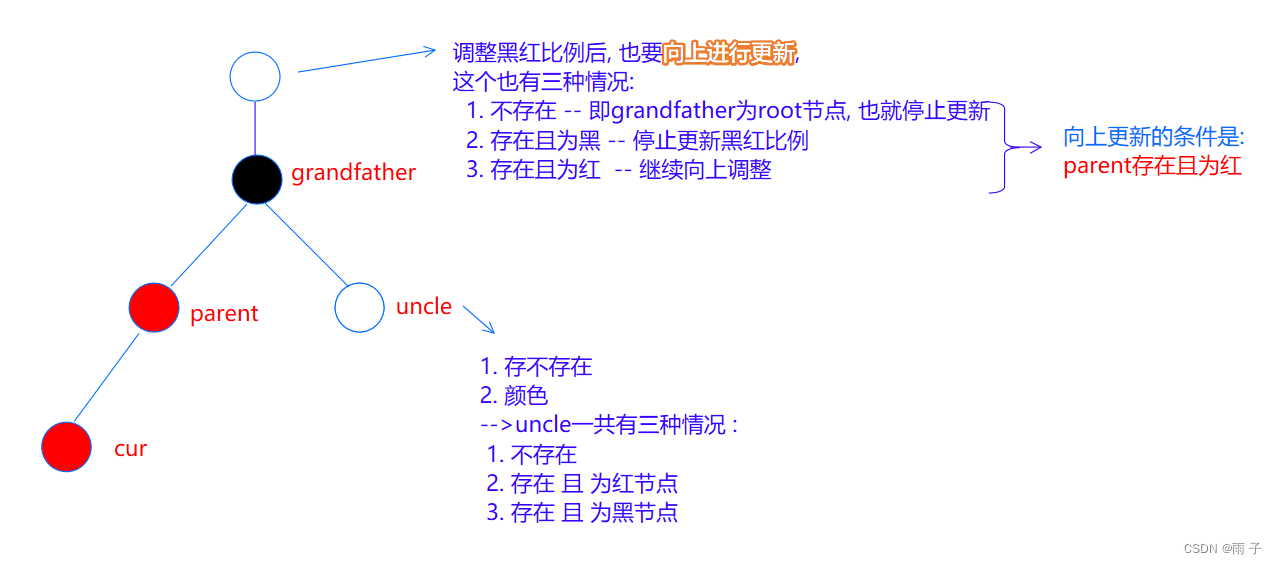
其实, 更新 当前节点到 祖宗节点这一条路径的 黑红比例 的本质是 看uncle的情况
首先, 要确定 uncle 位于grandfather的哪一侧 && uncle不一定存在, 但parent一定存在
⇒ 要确定parent 位于 grandfather的那一侧:
- parent 位于 grandfather的左侧
- parent 位于 grandfather的右侧
其次, 才是 uncle 的存在情况 以及 颜色情况
-
uncle存在且为红

-
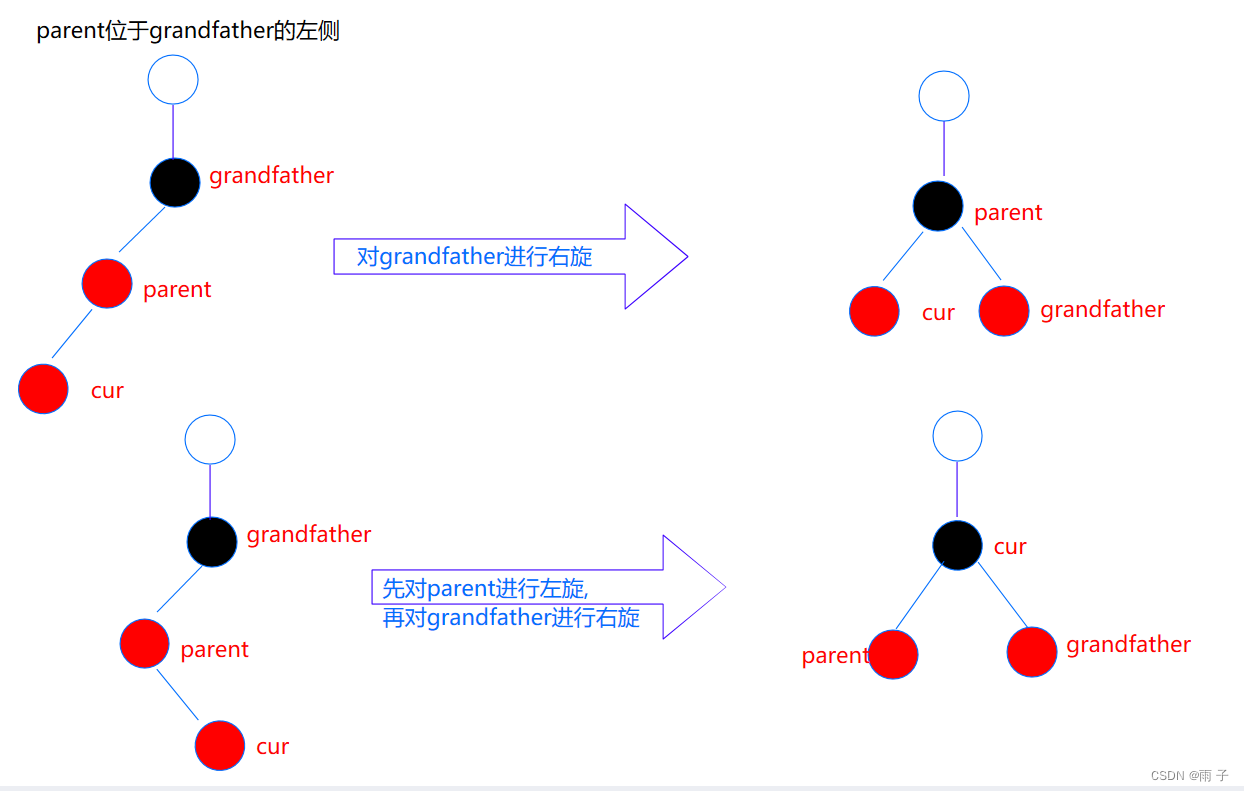
uncle不存在
如果 uncle不存在 ⇒cur为新增节点
- 如果cur不是新增节点, 那么 parent后面的节点必定是黑色的, 那么就违反了
每一条路径的黑色节点的个数是相同


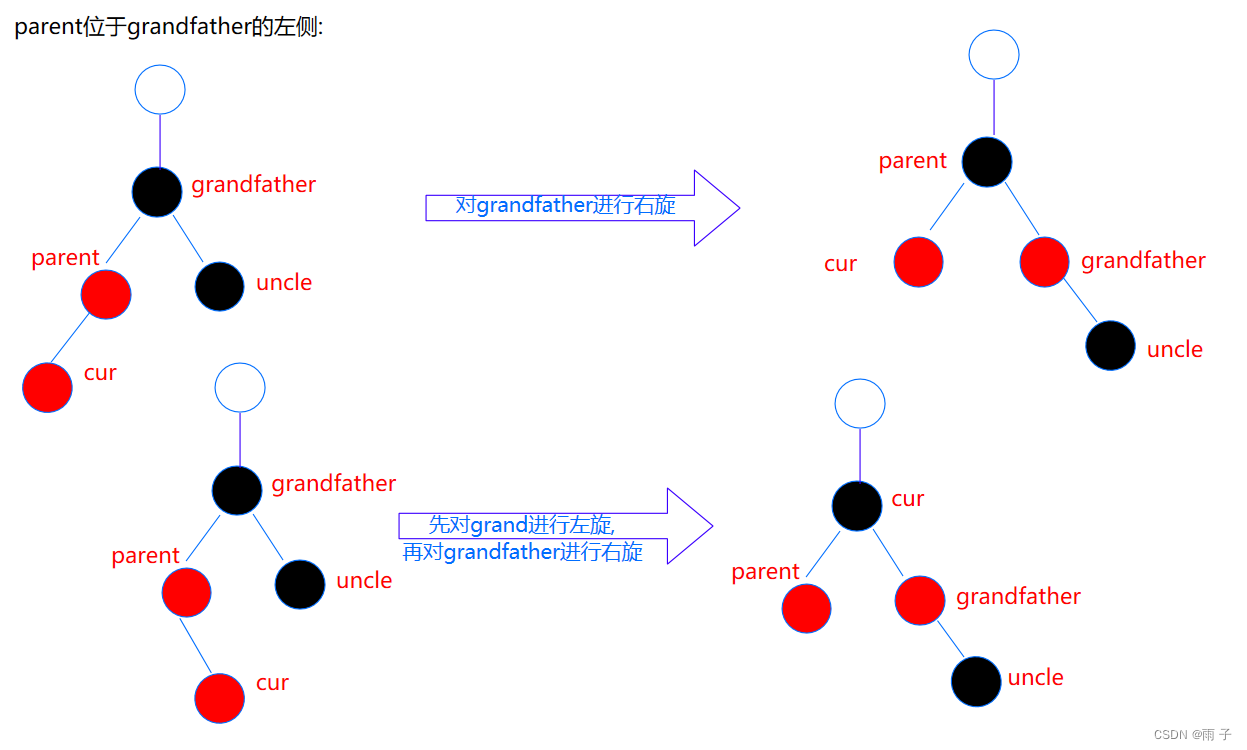
- uncle存在且为黑

如果uncle存在, 那么必定是黑色⇒ 那么 cur 也应该是黑色.
现在看到的cur 是红色的, 是由下面的更新上来的
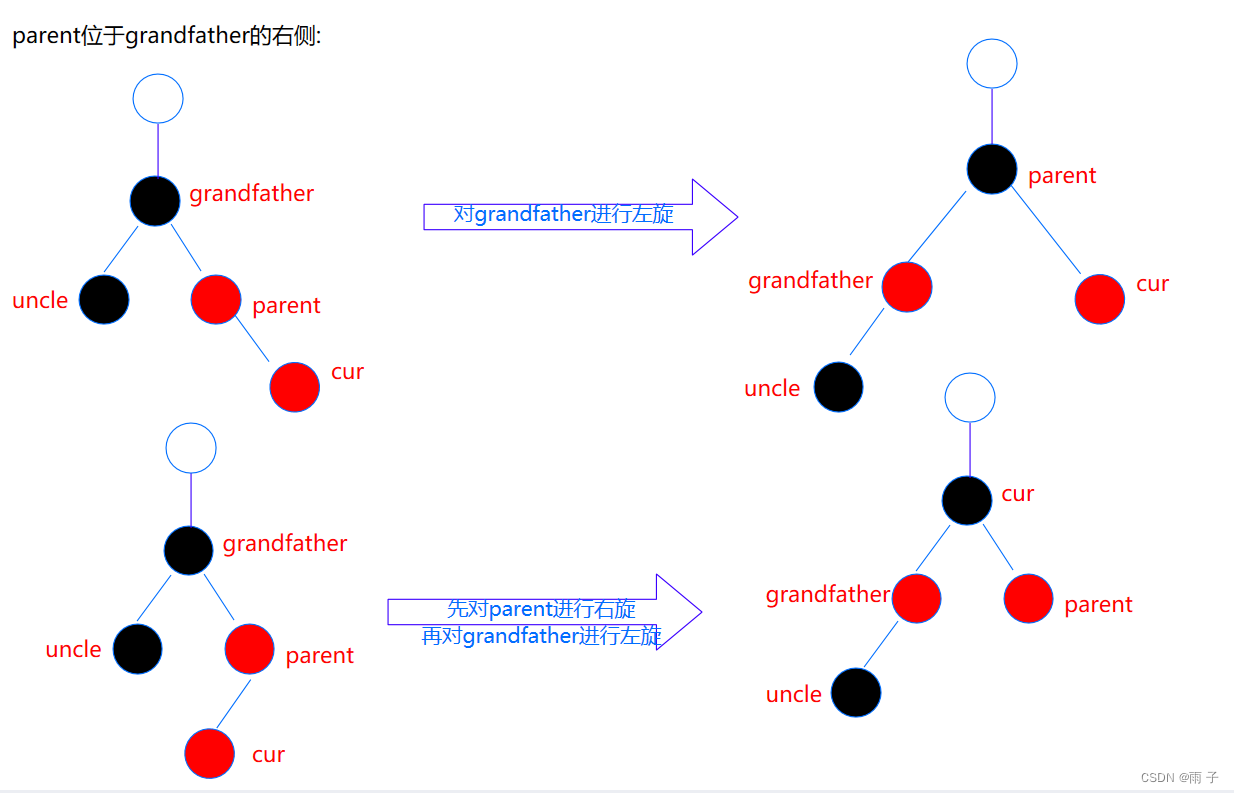
通过上面的图示, 我们得出 : 插入时, uncle主要分为两种情况
- uncle存在且为红 — —
由于更新后的头结点为红 ⇒ 我们需要继续向上更新下去 - uncle不存在 或 uncle存在且为黑 — —
由于更新后的头结点为黑 ⇒ 我们不需要继续向上更新下去
insert的完整代码
bool Insert(const pair<K, V> kv)
{if (_root == nullptr){// 根节点是黑色的_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = _root;Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 新建一个节点, 默认是红色cur = new Node(kv);cur->_color = RED;// 链接cur 和 parentif (cur->_kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 更改黑红比例// 父亲节点存在且为红, 才有机会继续向上更新下去while (parent && parent->_color == RED){Node* grandfather = parent->_parent;// parent 为 grandfather的左侧if (grandfather->_left == parent){Node* uncle = grandfather->_right;// u存在且为红if (uncle && uncle->_color == RED){// 颜色变化grandfather->_color = RED;parent->_color = uncle->_color = BLACK;// 继续向上调整cur = grandfather;parent = cur->_parent;}else // u不存在 或 u存在且为黑色{if (cur == parent->_left){RotateR(grandfather);grandfather->_color = RED;parent->_color = BLACK;}else{RotateL(parent);RotateR(grandfather);cur->_color = BLACK;grandfather->_color = RED;}// 更新后的头节点为黑色, 不需要继续向上更新break;}}// parent 为 grandfather的右侧else if (grandfather->_right == parent){Node* uncle = grandfather->_left;// u存在且为红if (uncle && uncle->_color == RED){// 颜色变化grandfather->_color = RED;uncle->_color = parent->_color = BLACK;// 继续向上调整cur = grandfather;parent = cur->_parent;}// u不存在 或 u存在且为黑色else{if (parent->_right == cur){RotateL(grandfather);parent->_color = BLACK;grandfather->_color = RED;}else{RotateR(parent);RotateL(grandfather);cur->_color = BLACK;grandfather->_color = RED;}// 更新后的头节点为黑色, 不需要继续向上更新break;}}else{assert("黑红比例失控!");}}// 有可能更新过程中会把 root更新为红色 // && root节点的颜色必须为黑色// -->暴力统一处理根节点的颜色_root->_color = BLACK;return true;
}
insert的验证
- 每一条路径的
黑节点个数相同⇒先找一个 基准值(root的左子树中 黑节点的个数)
如果后面的路径中 有的黑节点的个数 跟 基准值不同, 那就返回false. - 不能有连续的红节点 ⇒
当前节点为红节点, 那么父亲节点不能为红节点 root节点的颜色要为黑色
验证代码
// 外面调用接口
bool IsBalance()
{return IsBalance(_root);
}bool IsBalance(Node* root)
{if (root == nullptr)return true;// root节点为红, 就直接返回falseif (root->_color != BLACK){return false;}// 基准值 -- root左子树中的黑节点个数int benchmark = 0;Node* cur = _root;while (cur){if (cur->_color == BLACK)++benchmark;cur = cur->_left;}// 检查每条路径中黑节点个数 && 不能出现连续的红节点return CheckColour(root, 0, benchmark);
}bool CheckColour(Node* root, int blacknum, int benchmark)
{// 到叶子节点, 比较路径中黑节点的个数 和 基准值if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_color == BLACK){++blacknum;}// 不能存在连续的红节点if (root->_color == RED && root->_parent && root->_parent->_color == RED){cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);
}
Height
// 外面调用接口
int Height()
{return Height(_root);
}int Height(Node* root)
{if (root == nullptr)return 0;int left = Height(root->_left);int right = Height(root->_right);return left > right ? left + 1 : right + 1;
}
GetRotateCount
int GetRoateCount()
{return RotateCount;
}
测试程序
void rbt_test()
{const int N = 10000000;vector<int> v;v.reserve(N);srand((unsigned int)time(NULL));for (size_t i = 0; i < N; i++){int ret = rand();v.push_back(ret);// v.push_back(i);}muyu::RBTree<int, int> rbt;for (auto e : v){rbt.Insert(make_pair(e, e));// cout << "Insert:" << e << "->" << avl.Isbalance() << endl;}cout << "红黑树是否达标-> " << rbt.IsBalance() << endl;cout << "红黑树的高度-> " << rbt.Height() << endl;cout << "红黑树旋转的次数-> " << rbt.GetRoateCount() << endl;
}int main()
{rbt_test();return 0;
}
运行结果:
红黑树是否达标-> 1
红黑树的高度-> 19
红黑树旋转的次数-> 19119
源码
#pragma once#include<iostream>using namespace std;namespace muyu
{// 枚举enum Color{RED,BLACK};template<class K, class V>struct RBTreeNode{public:RBTreeNode(const pair<K, V> kv):_kv(kv){}public:pair<K, V> _kv;Color _color = BLACK;RBTreeNode<K, V>* _left = nullptr;RBTreeNode<K, V>* _right = nullptr;RBTreeNode<K, V>* _parent = nullptr;};template<class K, class V>class RBTree{typedef RBTreeNode<K, V> Node;public:RBTree(){}void RotateL(Node* parent){++RotateCount;Node* cur = parent->_right;Node* grandfather = parent->_parent;Node* curleft = cur->_left;// 旋转核心parent->_right = curleft;cur->_left = parent;// 更新父亲// 1. parent && curleftif (curleft){curleft->_parent = parent;}parent->_parent = cur;// 2.更新curif (grandfather == nullptr){cur->_parent = nullptr;_root = cur;}else{if (grandfather->_left == parent){grandfather->_left = cur;}else{grandfather->_right = cur;}cur->_parent = grandfather;}}void RotateR(Node* parent){++RotateCount;Node* cur = parent->_left;Node* grandfather = parent->_parent;Node* curright = cur->_right;// 旋转核心parent->_left = curright;cur->_right = parent;// 更新链接关系// 1. parent && currightif (curright){curright->_parent = parent;}parent->_parent = cur;// 2.更新curif (grandfather == nullptr){cur->_parent = nullptr;_root = cur;}else{if (grandfather->_left == parent){grandfather->_left = cur;}else{grandfather->_right = cur;}cur->_parent = grandfather;}}bool Insert(const pair<K, V> kv){if (_root == nullptr){// 根节点是黑色的_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = _root;Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 新建一个节点, 默认是红色cur = new Node(kv);cur->_color = RED;// 链接cur 和 parentif (cur->_kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 更改黑红比例while (parent && parent->_color == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;// u存在且为红if (uncle && uncle->_color == RED){// 颜色变化grandfather->_color = RED;parent->_color = uncle->_color = BLACK;// 继续向上调整cur = grandfather;parent = cur->_parent;}else // u不存在 或 u存在且为黑色{if (cur == parent->_left){RotateR(grandfather);grandfather->_color = RED;parent->_color = BLACK;}else{RotateL(parent);RotateR(grandfather);cur->_color = BLACK;grandfather->_color = RED;}break;}}else if (grandfather->_right == parent){Node* uncle = grandfather->_left;// u存在且为红if (uncle && uncle->_color == RED){// 颜色变化grandfather->_color = RED;uncle->_color = parent->_color = BLACK;// 继续向上调整cur = grandfather;parent = cur->_parent;}// u不存在 或 u存在且为黑色else{if (parent->_right == cur){RotateL(grandfather);parent->_color = BLACK;grandfather->_color = RED;}else{RotateR(parent);RotateL(grandfather);cur->_color = BLACK;grandfather->_color = RED;}break;}}else{assert("黑红比例失控!");}}// 暴力统一处理根节点的颜色_root->_color = BLACK;return true;}int Height(){return Height(_root);}int Height(Node* root){if (root == nullptr)return 0;int left = Height(root->_left);int right = Height(root->_right);return left > right ? left + 1 : right + 1;}bool CheckColour(Node* root, int blacknum, int benchmark){if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_color == BLACK){++blacknum;}if (root->_color == RED && root->_parent && root->_parent->_color == RED){cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;if (root->_color != BLACK){return false;}// 基准值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_color == BLACK)++benchmark;cur = cur->_left;}return CheckColour(root, 0, benchmark);}int GetRoateCount(){return RotateCount;}private:Node* _root = nullptr;int RotateCount = 0;};
}
十年磨一剑,霜刃未曾试。
今日把示君,谁有不平事。
— — 贾岛《剑客》

![[工业自动化-10]:西门子S7-15xxx编程 - PLC主站 - 信号量:数字量](https://img-blog.csdnimg.cn/e0fd4faa680a4a6086eeb914daae5059.png)
![轻量日志管理方案-[EFK]](https://img-blog.csdnimg.cn/cb4a4b369dec4ac4afe46ca0b1a4f3e1.png)