LabVIEW示波器连续触发编程
niScopeEX Fetch Forever范例利用了如何设置硬件和驱动的优点来进行连续采集。
当NI-SCOPE设备被设置为采集预触发扫描,设备上的板载内存被用作一个环形缓冲。这样,无论触发何时到来,设备都可以追踪和检索所有要求的预触发点数。Fetch Forever范例利用了这样的优势来设置一个触发到的单记录的采集。因为板载缓冲是连续的填写并且等待一个触发来决定预触发和后触发采样点,所以单次采集永远不完成。范例直接从板载缓冲中连续读取数据。
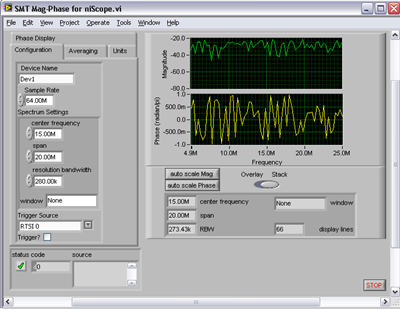
如果一个软件或者硬件触发被接收到,单次采集会采集到多于后触发扫描要求的点。下一次的取点会返回预触发和后触发的采样点,并且结束单次采样。这就是范例配置了一个触发(配置设备采集预触发点数)并且从来不发送触发原因。
如果应用需要一个连续的预触发采集,需要采用以下两种选择:
采用niScopeEX MultiRecord Fetch More Than Available Memory范例。该范例为硬件配置了一个多记录的采集。然后,可以配置触发源来触发每一个新的记录。局限性是必须采集有限的点数,这是因为驱动会返回一个时间戳信息,当使用多记录并且必须知道该为时间戳信息分配多少的存储。需要设置Enable Records>Memory属性为真。这样会转移板载存储到RAM中来。此时,在得到一个内存不足错误之前,主机可用内存的大小限制了记录的大小。
使用niScopeEX Configured Acquisition替代,该范例连续重配置了一个单记录的采集并且支持触发。唯一的局限是电脑处理器能否跟上需要的重配置速率。如果关心效率,可以修改范例并且移动某些或者所有的配置VI到While循环外面来。
这是LabVIEW的一个功能介绍,更多的使用方法与开发案例,欢迎登录官网,了解更多信息。有需要LabVIEW项目合作开发,请与我们联系。