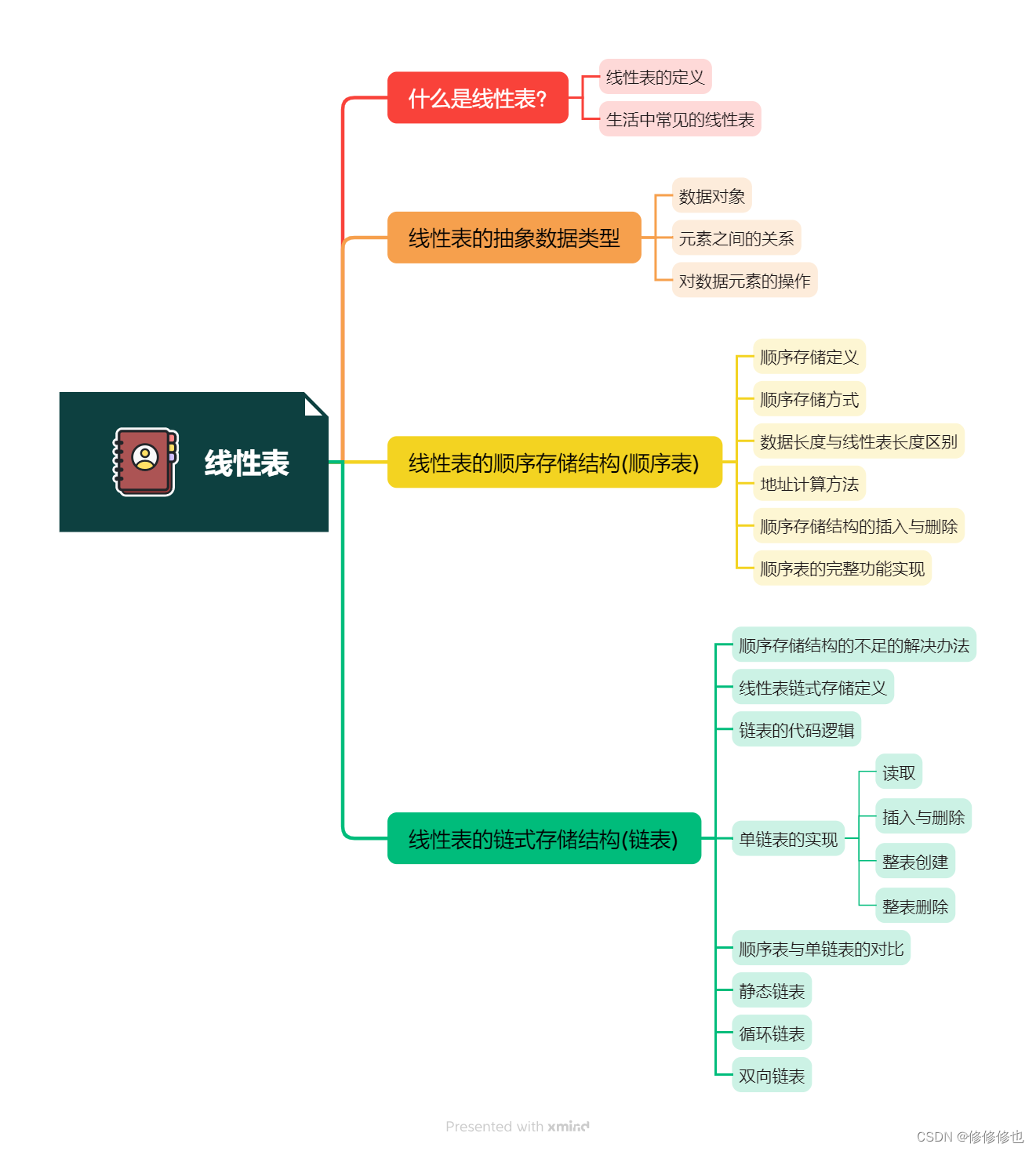
这是关于3Blue1Brown "线性代数的本质"的学习笔记。

向量是什么

可以是一个箭头，可以是一组实数，即一个坐标对。

箭头在高维（4维，甚至更高）空间，概念比较模糊。

坐标对用数值表示，相对清晰。但数值对依赖于选取的基向量。而且线性代数的核心话题，比如行列式、特征向量等，又和所选坐标系没有关系。

行列式说的是一个变换对面积的缩放比例，特征向量则是在变换中留在它所张成的空间中的向量。坐标系怎么选都不会改变这二者最根本的值。

函数

从某种意义上说，函数实际上只是另一种向量。
$$\begin{gathered} (f+g)(x)=f(x)+g(x) \\ (2f)(x)=2f(x) \end{gathered}$$
用箭头表示的向量的线性代数的所有特征，比如线性变换、数乘、点积等等，都能原封不动地用在函数上。

比如函数的变换，是输入一个函数，并把它变成另一个函数，这的一个例子就是导数，它将函数变换到另一个函数。这在函数中，一般称为算子，而不是变换。这是函数的变换，但怎么算是“线性”的？

什么是线性

满足以下两条性质的变换是线性的：

• 可加性：对两个向量进行相加，然后对它们的和进行变换，得到的结果和将变换后的两个向量相加一致。
• 成比例性：将一个向量与某个数相乘，然后对其进行变换，得到的结果和变换后的向量与这个数相乘一致

即线性变换保持向量加法运算和数乘运算。

前面讨论的网格线平行且等距分布，是这两条性质在二维平面这一特殊情况下的体现。

图1 线性的严格定义

因此，求导是线性运算。满足可加性和数乘性（成比例）质。

推论

一个向量可以表示为基向量以某种方式进行线性组合，所以，求一个向量变换后的结果，实际上就是求出变换后的基向量以相同方式进行线性组合的结果。

向量空间

箭头、一组数、函数等，它们构成的集合被称为“向量空间”。
向量空间中的对象满意以下规则（公理）：

图2 向量加法和数乘规则