文章目录
- 🍉题目1:反转链表
- 🍉解析
- 🍌解法一:创建一个新链表
- 🍌解法二:直接操作原链表
- 🍉题目2:返回中间节点
- 🍌解法一:快慢指针
- 🍌解法二:两次遍历
🍉题目1:反转链表
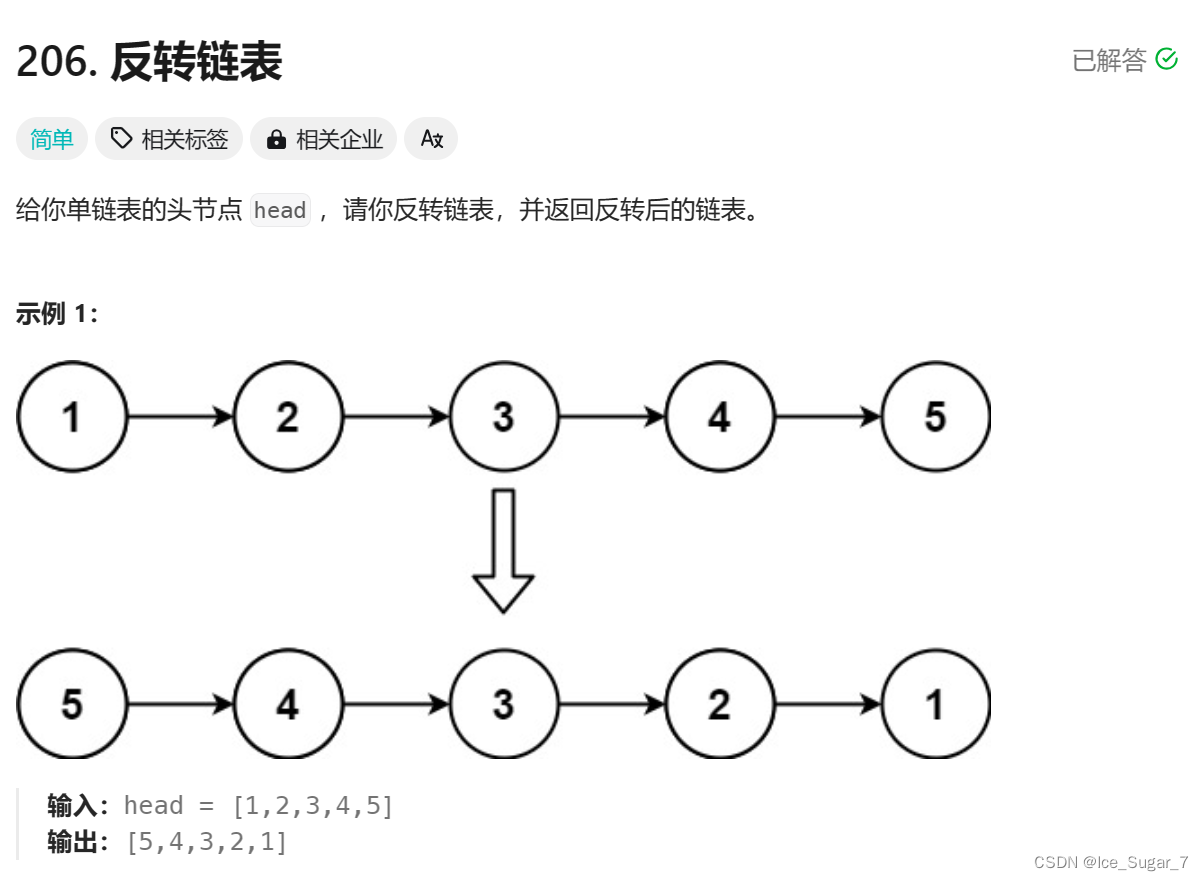
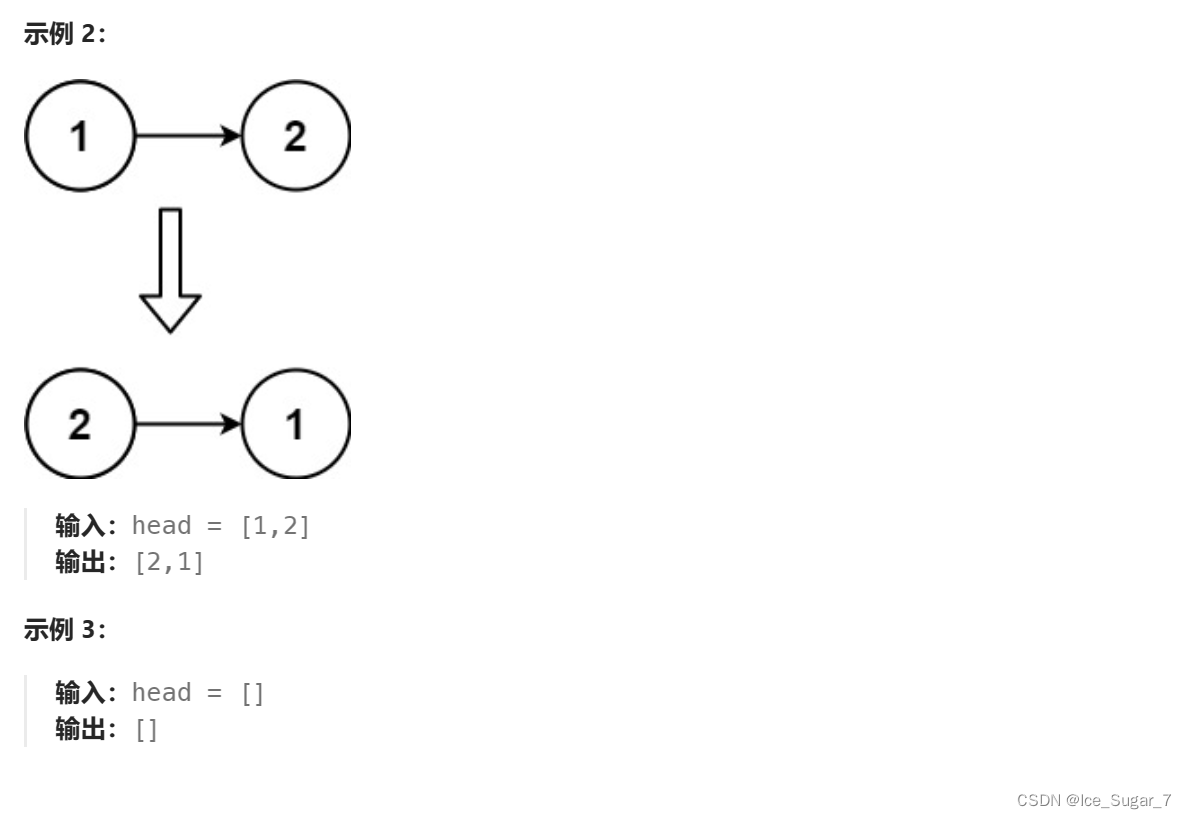
🍉解析
🍌解法一:创建一个新链表
这种解法算是比较通用的,就题目如果要求要对某个对象进行操作,那我们一般可以考虑创建一个新的对象,按照题目要求把符合条件的元素放进去。
现在要反转的话,那就相当于先遍历原链表,每遇到一个节点就头插插入新链表(越后面的节点插入后就到新链表越靠前的位置,这应该很好理解)
如何创建新链表?首先得先定义一个指针:newhead,newhead 是新链表的头节点。第一次插入得考虑新链表为空的情况
代码如下:
struct ListNode* reverseList(struct ListNode* head) {struct ListNode* cur = head;struct ListNode* newhead = NULL;while (cur){ struct ListNode* next = cur->next; //头插前先用next保存cur下次要指向的节点//头插cur->next = newhead;newhead = cur;cur = next;}return newhead;
}
🍌解法二:直接操作原链表
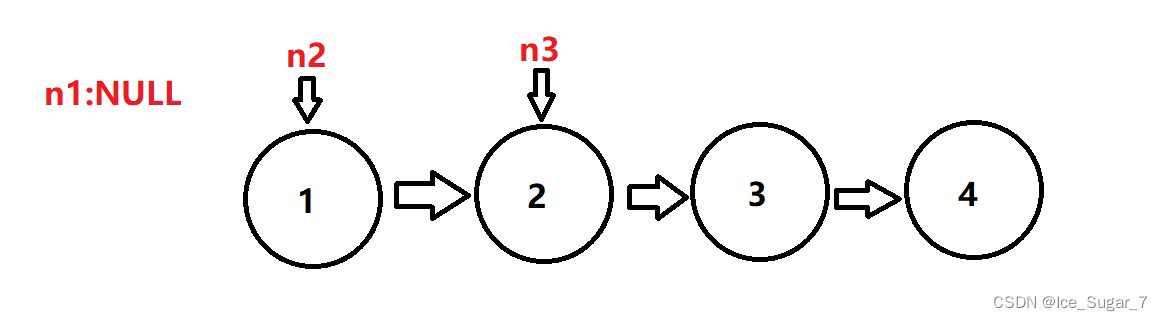
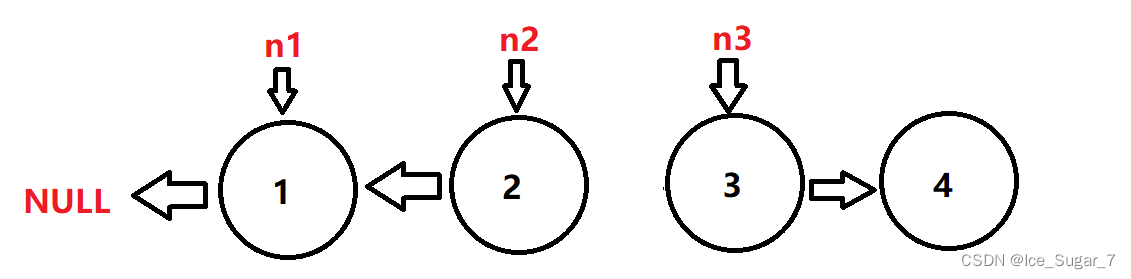
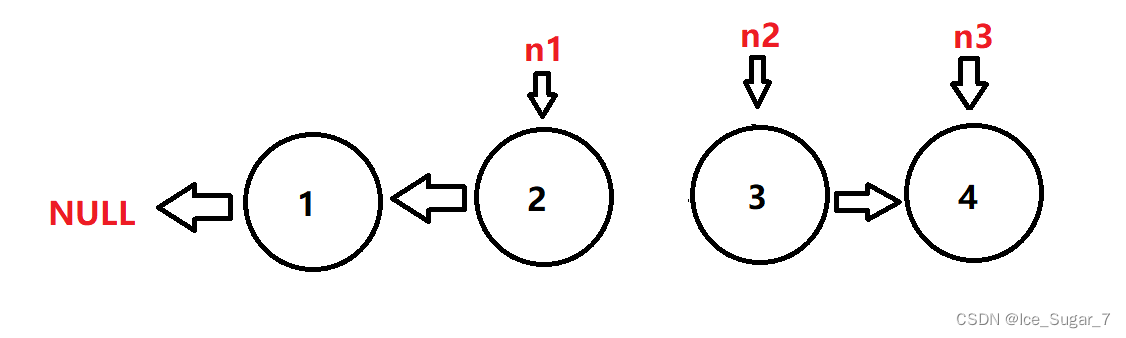
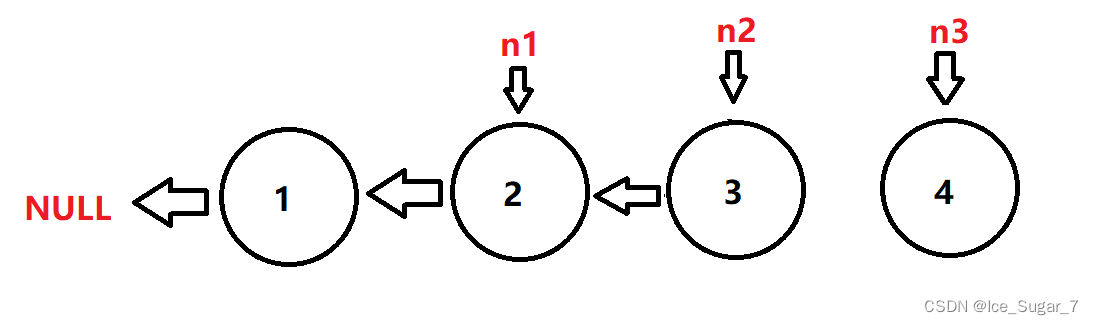
设置三个变量n1、n2 和 n3,每次将 n2 所指的节点的 next 指向 n1 ,然后 n1 和 n2 和 n3 继续往前走,直到 n3 为空(即下图第四个节点的next)。
这个思路简而言之就是:把一个节点的next改为指向前一个节点。
为啥要弄一个n3呢?因为 n2 不仅要让它的 next 指向 n1,同时你还要让 n2 往后走,而往后走也要用到next,这两个都会改变 n2 或者 n2->next ,所以就用一个 n3 保存 n2 的next。
下面是代码:
typedef struct ListNode ListNode;
struct ListNode* reverseList(struct ListNode* head) {if(!head){return NULL;}ListNode* n1 = NULL;ListNode* n2 = head;ListNode* n3 = head->next;while(n2) {n2->next = n1;n1 = n2;n2 = n3;if(n3) {n3 = n3->next;}}return n1;
}
注意:n3 在往前推进的时候要先判断是否为空,因为它为空的话就没法解引用,也就没有next了(这个点在前面单链表那篇文章中见到不少次了)
🍉题目2:返回中间节点
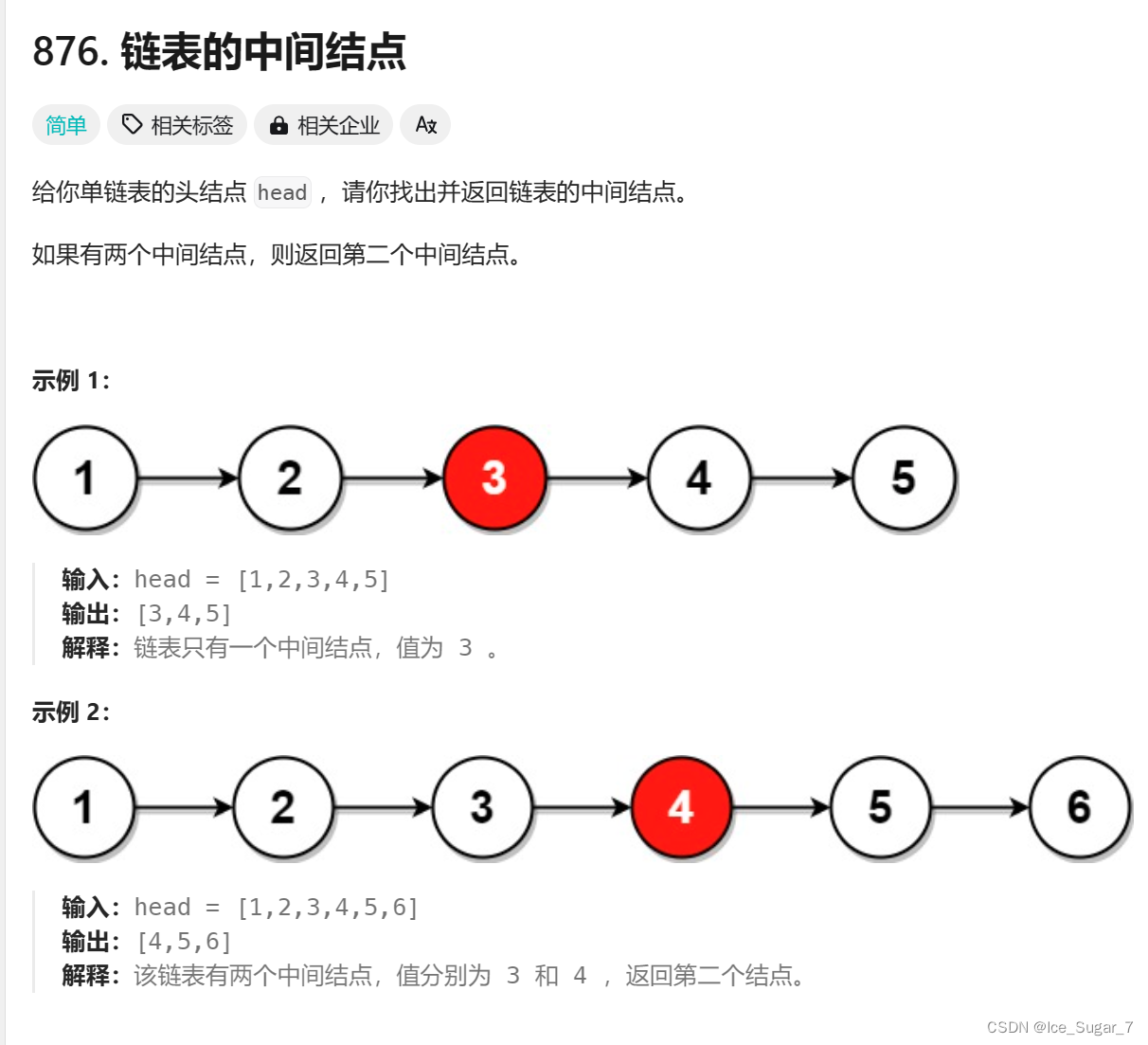
🍌解法一:快慢指针
顾名思义,就是弄两个指针,分别记为 fast 和 slow,其中快指针一次走两个单位;慢指针一次走一个。这样,当快指针遍历完链表时,慢指针刚好到中间的节点。若为偶数个节点,题目说返回第二个中间节点,你去画图会发现按这种解法,slow刚好走到第二个。
这种方法的原理也很简单,就是数学上的“路程差”。
typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head) {ListNode* slow = head,*fast = head;while(fast && fast->next) {fast = fast->next->next;slow = slow->next;}return slow;
}
快指针和慢指针的速度你可以根据需求自定义,而非说快指针的速度一定是慢指针的两倍。这种思想除了用于解决中间节点问题,还可以解决找倒数第 n 个节点的问题。
比如我们要找某链表倒数第三个节点,那就可以让快指针先走三步,此后快慢指针每次都走一步,快指针走完时(终止条件是快指针为空)
🍌解法二:两次遍历
先定义一个计数器count,然后第一次遍历每过一个节点count就+1,然后第二次使用for循环遍历count / 2次,循环具体要走多少次,你举个特例就可以推出来了(比如3个节点,4个节点)
typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head) {ListNode* pcur = head;int count = 1;while(pcur->next) {pcur = pcur->next;count++;}pcur = head;for(int i = 0;i<count/2;i++){pcur = pcur->next;}return pcur;
}










![论文阅读[121]使用CAE+XGBoost从荧光光谱中检测和识别饮用水中的有机污染物](https://img-blog.csdnimg.cn/5c7b9b90e3ba4c12a806aedc4d9c1e8c.png)


