NovelD:一种简单而有效的探索准则

1、Motivation

针对稀疏奖励环境下的智能体探索问题，许多工作中采用各种内在奖励(Intrinsic Reward)设计来指导困难探索环境中的探索 ，例如：

• ICM：基于前向动力学模型的好奇心驱动探索
• RND：基于随机网络蒸馏驱动的探索
• Count-Based：基于伪计数驱动的探索

但是本文作者从实验中观察到，如果有多个感兴趣的区域，这些方法有时会很快使智能体被困在一个区域，而无法充分探索其他区域。

2、Introduction

算法使用轨迹中连续状态的NovelD，这个标准在探索和未探索区域之间的边界上提供了很大的内在奖励。

NovelD有以下几点优势：

1. 几乎没有超参数
2. 是一种单阶段方法，可以很容易地与任何策略学习方法(例如PPO)相结合
3. NovelD是渐近一致的:在充分探索之后，它的IR会消失，而RIDE和AMIGo这样的方法则不会。
4. 与基于计数的方法和RND相比，NovelD优先考虑未探索的边界状态，产生更有效和更广泛的探索模式。

3、方法

在本篇文章中，每一次执行动作后得到的reward表示为：
$$r_t=r_t^e+\alpha r_t^i$$
intrinsic reward被定义为：
$$r^i({\mathbf{s}}_t,{\mathbf{a}}_t,{\mathbf{s}}_{t+1})=\max \left[\text{novelty}({\mathbf{s}}_{t+1})-\alpha \cdot \text{novelty}({\mathbf{s}}_t),0\right]$$
其中α是比例因子，定义一个被探索过的区域为：
{ s : n o v e l t y ( s ) ≤ m } \{\mathbf{s}:\mathrm{novelty}(\mathbf{s})\leq m\} {s:novelty(s)≤m}
当智能体的探索超过这个区域的边界时，NovelD会给予intrinsic reward。从公式(2)可以看出，当智能体从新状态转回熟悉的状态时，会截取IR以避免负IR。

从等式(2)可以看出，只有当智能体跨越边界时才会关系到IR，当st和st+1都是熟悉的或者陌生的状态时，它们的区别会很小。

但是简单的使用等式(1)会导致智能体在新状态st+1和旧状态st之间来回切换，对此NovelD设置了更为激进的限制：智能体只有在一个episode里第一次访问状态s时才会获得奖励。于是NovelD的intrinsic reward为：
r i ( s t , a t , s t + 1 ) = max ⁡ [ novelty ( s t + 1 ) − α ⋅ novelty ( s t ) , 0 ] ∗ I { N e ( s t + 1 ) = 1 } r^i(\mathbf{s}_t,\mathbf{a}_t,\mathbf{s}_{t+1})=\max\left[\text{novelty}(\mathbf{s}_{t+1})-\alpha\cdot\text{novelty}(\mathbf{s}_t),0\right]*\mathbb{I}\{N_e(\mathbf{s}_{t+1})=1\} ri(st​,at​,st+1​)=max[novelty(st+1​)−α⋅novelty(st​),0]∗I{Ne​(st+1​)=1}
Ne代表一个episode中的状态s的计数，每个episode会重置这个计数。而novelty算子是life-long的。

novelty使用RND方法来计算：
$$\mathrm{novelty}({\mathbf{s}}_t)=\mathrm{novelty}({\mathbf{s}}_t;\mathbf{w}):=\Vert \varphi ({\mathbf{s}}_t)-{\varphi }_{\mathbf{w}}^{\prime }({\mathbf{s}}_t){\Vert }_2$$
计算出st的novelty后，就对w执行一次更新来最小化novelty(st;w)。

NovelD是一个一致性算法，经过充分的探索，内在奖励收敛于0。

对于将intrinsic reward定义为：
$$\Vert \psi ({\mathbf{s}}_t)-\psi ({\mathbf{s}}_{t+1})\Vert$$
的方法，通常会面临渐进不一致性问题，这是因为在足够多的探索使ψ收敛后，由于神经网络无法完全拟合的特性，智能体总是可以获得非零IR，即当N—>∞时IR永远不—>0。因此，学习策略没有最大化外部奖励r_e，偏离了强化学习的目标。

但是NovelD方法是渐进一致的。

4、实验

1、对于所有实验，使用PPO作为基础RL算法，同时将NovelD与其他各种生成intrinsic reward的方法进行比较。

在实验的一半任务中，所有的基线结果都是零奖励。在《NetHack》中，NovelD取得了SOTA。

实验主要使用MiniGird中的三个具有挑战性的环境:多房间(MR)，关键走廊(KC)和受阻迷宫(OM)。

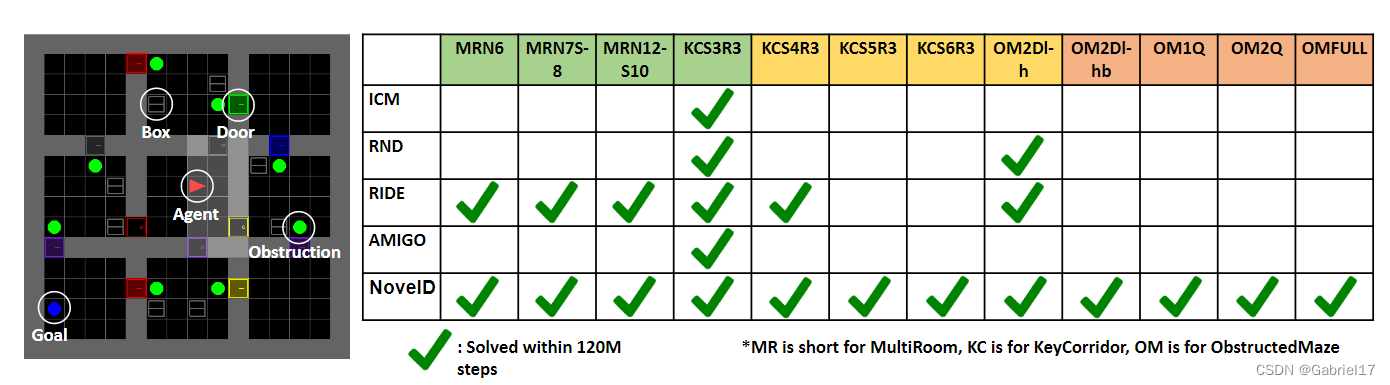
可以从图中看到，NovelD设法解决了MiniGrid中的所有静态环境。相比之下，所有的基线只能解决中等水平的任务，而不能在更困难的任务上取得任何进展。

2、仅在环境中使用IR进行探索(无外部奖励)，NovelD导致了更集中的边界探索和更广泛的状态覆盖。

为了研究NovelD是否在MiniGrid中产生更广泛的状态覆盖，实验在一个固定的MRN7S8环境中测试了NovelD和RND。同时，定义了两个指标来衡量勘探策略的有效性：

1. 每个状态的探视次数都超过训练次数

2. 每个房间的访问熵：
   $$\mathcal{H}({\rho }^{\prime }(\mathbf{s}))\text{ where }{\rho }^{\prime }(\mathbf{s})=\frac{N(\mathbf{s})}{{\sum }_{\mathbf{s}\in {\mathcal{S}}_r}N(\mathbf{s})}$$

实验结果显示，NovelD的每个房间熵分布大于RND。这表明与RND相比，NovelD鼓励对状态进行更统一的探索。

实验说明，当两个房间之间的门成为探索的瓶颈时，NovelD的IR专注于解决这个问题。

3、消融实验

文章设计实验寻找最佳的比例和裁剪系数，公式：
$$r^i({\mathbf{s}}_t,{\mathbf{a}}_t,{\mathbf{s}}_{t+1})=\max \left[\text{novelty}({\mathbf{s}}_{t+1})-\alpha \cdot \text{novelty}({\mathbf{s}}_t),\beta \right]$$
实验得出当α=0.5，β=0时效果最好。

文章设计实验验证不同特征提取方式对NovelD效果的影响，分别有：ICM、Random、DBC以及Successor Features。最终发现只有Random和Successor Features表现得还不错。

5、结论

NovelD方法也适用于随机环境，虽然到达随机环境的边界本身是一个难题，但通过在边界状态上设置高IR并使用RL算法训练代理，策略将更频繁地到达这些边界状态。

NovelD方法由于采用RND方法来进行新颖性度量，所以对于白噪声问题有一定的缓解，而实验也表明在《MiniGrid》、《Atari Games》和《NetHack》中，都没有看到由于电视噪音问题导致的NovelD的性能下降。

在多种环境中，NovelD显示了更广泛的状态覆盖，并将IR的重点放在边界状态上。

6、留存的问题

没有在一些连续RL领域测试NovelD的性能。