import numpy as np
from matplotlib.font_manager import FontProperties
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
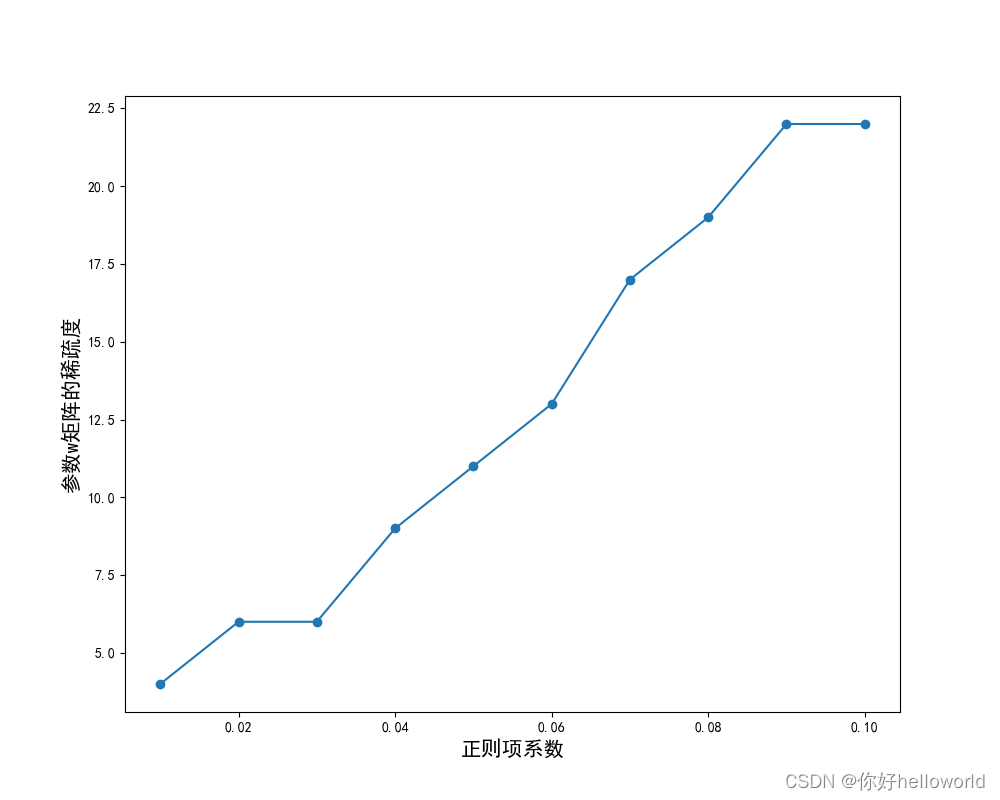
import matplotlib.pyplot as pltclass Lasso():def __init__(self):pass# 数据准备def prepare_data(self):# 生成样本数据X, y = make_regression(n_samples=40, n_features=80, random_state=0, noise=0.5)# 划分数据集X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)return X_train, X_test, y_train.reshape(-1,1), y_test.reshape(-1,1)# 参数初始化def initialize_params(self, dims):w = np.zeros((dims, 1))b = 0return w, b# 定义L1损失函数def l1_loss(self, X, y, w, b, alpha):num_train = X.shape[0] # 样本数num_feature = X.shape[1] # 特征数y_hat = np.dot(X, w) + b # 回归预测数据# 计算损失loss = np.sum((y_hat - y) ** 2) / num_train + alpha * np.sum(np.abs(w)) # 修改此处# 计算梯度,即参数的变化dw = np.dot(X.T, (y_hat - y)) / num_train + alpha * np.sign(w) # 修改此处db = np.sum((y_hat - y)) / num_trainreturn y_hat, loss, dw, dbdef lasso_train(self, X, y, learning_rate, epochs, alpha):loss_list = []w, b = self.initialize_params(X.shape[1])# 归一化特征X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)for i in range(1, epochs):y_hat, loss, dw, db = self.l1_loss(X, y, w, b, alpha)# 更新参数w += -learning_rate * dwb += -learning_rate * dbloss_list.append(loss)# if i % 300 == 0:# print('epoch %d loss %f' % (i, loss))params = {'w': w,'b': b}grads = {'dw': dw,'db': db}return loss, loss_list, params, grads# 根据计算的得到的参数进行预测def predict(self, X, params):w = params['w']b = params['b']y_pred = np.dot(X, w) + breturn y_predif __name__ == '__main__':lasso = Lasso()X_train, X_test, y_train, y_test = lasso.prepare_data()alphas=np.arange(0.01,0.11,0.01)wc=[]#统计参数w中绝对值小于0.1的个数,模拟稀疏度for alpha in alphas:# 参数:训练集x,训练集y,学习率,迭代次数,正则化系数loss, loss_list, params, grads = lasso.lasso_train(X_train, y_train, 0.02, 3000,alpha)w=np.squeeze(params['w'])count=np.sum(np.abs(w)<1e-1)wc.append(count)# 设置中文字体plt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = Falseplt.figure(figsize=(10, 8))plt.plot(alphas, wc, 'o-')plt.xlabel('正则项系数',fontsize=15)plt.ylabel('参数w矩阵的稀疏度',fontsize=15)plt.show()