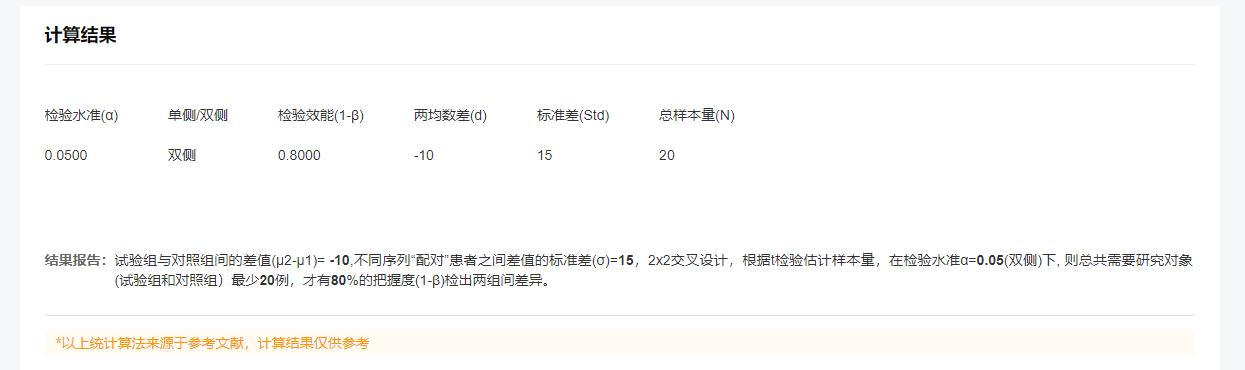
1. 背景
回归方程与回归系数的显著性检验
2. statsmodels 库
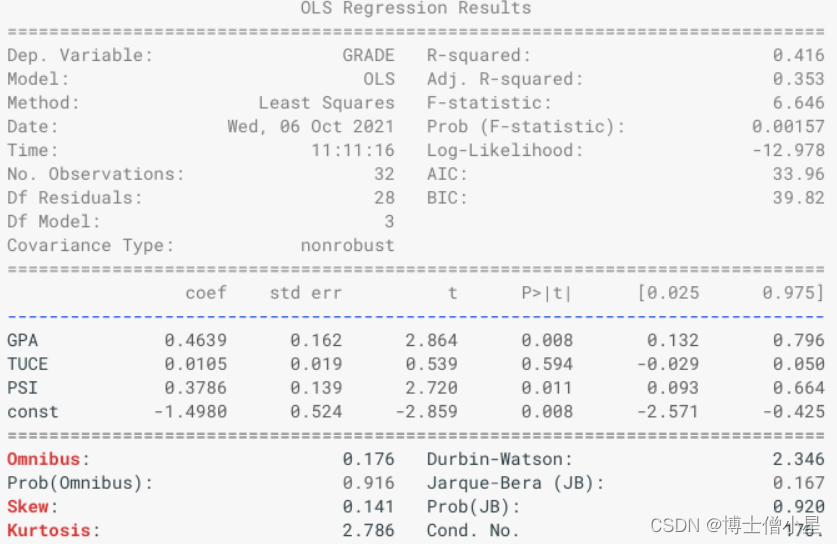
statsmodels库可以用来做逻辑回归、线性回归。并且会在summary中给出显著性检验的结果。最终我们想要的就是如下图的报告。
3. 计算过程
如果我们使用的sklearn构建的逻辑回归就没有办法直接输出这个报告,所以需要自己计算这个表中的信息。
3.1 先用statemodels计算作为对比
import pandas as pd
from sklearn.datasets import load_boston
from scipy import stats
import statsmodels.api as sm
import numpy as np''' 数据demo'''
boston = load_boston()
X = pd.DataFrame(boston.data, columns=boston.feature_names)
y = pd.DataFrame(boston.target, columns=['target'])X = sm.add_constant(X) # 添加常数项
model = sm.OLS(y, X)
results = model.fit()
y_pred = pd.DataFrame(model.predict(results.params, X),columns=['pred'])
print(results.summary())''''''输出结果:
OLS Regression Results
==============================================================================
Dep. Variable: target R-squared: 0.741
Model: OLS Adj. R-squared: 0.734
Method: Least Squares F-statistic: 108.1
Date: Thu, 04 Nov 2021 Prob (F-statistic): 6.72e-135
Time: 11:07:53 Log-Likelihood: -1498.8
No. Observations: 506 AIC: 3026.
Df Residuals: 492 BIC: 3085.
Df Model: 13
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 36.4595 5.103 7.144 0.000 26.432 46.487
CRIM -0.1080 0.033 -3.287 0.001 -0.173 -0.043
ZN 0.0464 0.014 3.382 0.001 0.019 0.073
INDUS 0.0206 0.061 0.334 0.738 -0.100 0.141
CHAS 2.6867 0.862 3.118 0.002 0.994 4.380
NOX -17.7666 3.820 -4.651 0.000 -25.272 -10.262
RM 3.8099 0.418 9.116 0.000 2.989 4.631
AGE 0.0007 0.013 0.052 0.958 -0.025 0.027
DIS -1.4756 0.199 -7.398 0.000 -1.867 -1.084
RAD 0.3060 0.066 4.613 0.000 0.176 0.436
TAX -0.0123 0.004 -3.280 0.001 -0.020 -0.005
PTRATIO -0.9527 0.131 -7.283 0.000 -1.210 -0.696
B 0.0093 0.003 3.467 0.001 0.004 0.015
LSTAT -0.5248 0.051 -10.347 0.000 -0.624 -0.425
==============================================================================
Omnibus: 178.041 Durbin-Watson: 1.078
Prob(Omnibus): 0.000 Jarque-Bera (JB): 783.126
Skew: 1.521 Prob(JB): 8.84e-171
Kurtosis: 8.281 Cond. No. 1.51e+04
==============================================================================3.2 自己代码做
计算的函数
def func_sign_testing_LRCoef(X, y_pred, y_true, Coef):'''逻辑回归系数的显著性检验:param X: 原始数据,行为样本,列为特征(注意,如果你的Coef比特征多一列,那么应该在数据上加一列const X.insert(0, 'const', 1) # 添加常数项):param y_pred: 模型的预测结果:param y_true: 数据的真实结果:param Coef: 逻辑回归的回归系数:return: 返回报告包含'coef','std error','tval','pval','lower alpha','upper alpha''''# y_pred = y_pred.values# y_true = y.values# Coef = results.params.valuesn, p = X.shapep = p - 1 # p 为特征数# X.insert(0, 'const', 1) # 添加常数项# SSR = np.dot(y_pred - y_true.mean(), y_pred - y_true.mean())y_pred = np.squeeze(y_pred)y_true = np.squeeze(y_true)Coef = np.squeeze(Coef)SSR = np.dot(np.squeeze(y_pred) - np.squeeze(y_true).mean(),np.squeeze(y_pred) - np.squeeze(y_true).mean())SSE = np.dot(np.squeeze(y_pred) - np.squeeze(y_true),np.squeeze(y_pred) - np.squeeze(y_true))# SSE = np.dot(y_pred - y_true, y_pred - y_true)# 先计算回归方程的显著性f_val = (SSR / p) / (SSE / n - p - 1)f_pval = stats.f.sf(f_val, p, n - p - 1)print("LR F", f_val)print("LR p", f_pval)# 单个参数的显著性检验# print(X.columns)ttest_result = pd.DataFrame(None, index=X.columns,columns=['coef', 'std error', 'tval', 'pval', '[lower alpha', 'upper alpha]'])ttest_result.loc[:, 'coef'] = np.squeeze(Coef)error = np.dot(y_true - y_pred, y_true - y_pred)S = np.array(np.linalg.inv(np.dot(X.T, X)))for i, col in enumerate(X.columns):RMSE = np.sqrt(error / n - p - 1)tval = Coef[i] / np.sqrt((error / (n - p - 1)) * S[i][i])ttest_result.loc[col, 'tval'] = tval# pval_test = stats.t.sf(np.abs(tval), df=492) * 2std_error = Coef[i] / tval # np.sqrt(S[i][i]) * RMSE# 其实表里的t检验值就剩余表里的b系数除以std error哦,t=b/std errorttest_result.loc[col, 'std error'] = std_errorpval = stats.t.sf(np.abs(tval), df=(n - p - 1)) * 2ttest_result.loc[col, 'pval'] = pval[lower_a, upper_a] = stats.norm.ppf(q=[0.025, 0.975], loc=Coef[i], scale=std_error)ttest_result.loc[col, '[lower alpha'] = lower_attest_result.loc[col, 'upper alpha]'] = upper_areturn ttest_result调用函数
boston = load_boston()
X = pd.DataFrame(boston.data, columns=boston.feature_names)
y = pd.DataFrame(boston.target, columns=['target'])
X = sm.add_constant(X) # 添加常数项
model = sm.OLS(y, X)
results = model.fit()
y_pred = pd.DataFrame(model.predict(results.params, X),columns=['pred'])# results.params.values 将训练得到的coef系数给进函数
func_sign_testing_LRCoef(X, y_pred, y, results.params.values)