解法：

将01序列置于坐标轴上，起始点为原点。0表示向右走，1表示向上走。这样就可以将前缀0的个数不少于1的个数就可以转换为路径上的点，横坐标大于纵坐标，也就是求合法路径个数。

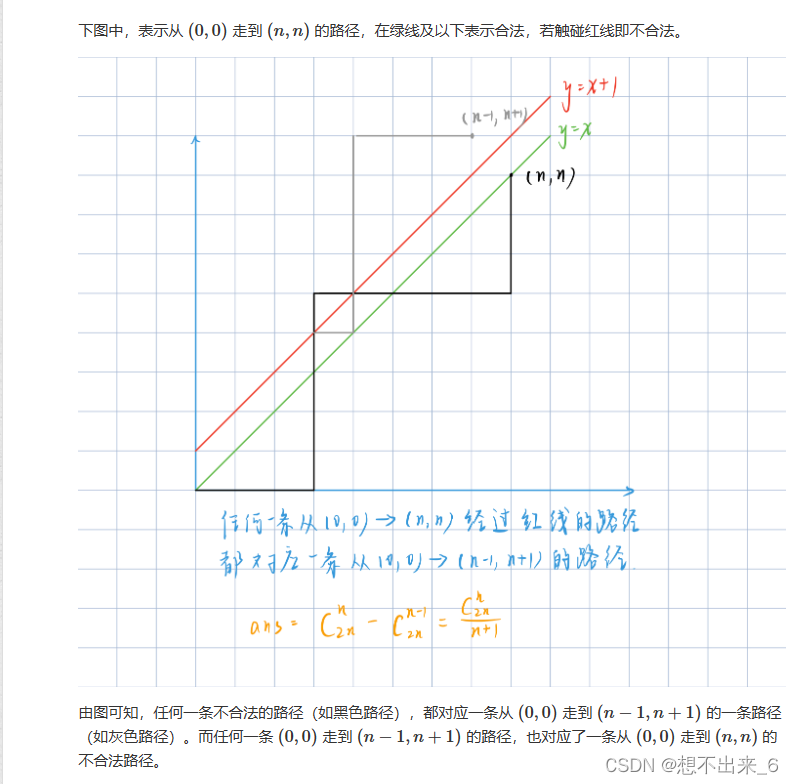
注意题目mod的数是质数，所以可以使用快速幂求逆元，若不是质数，则需要使用扩展欧几里得算法求逆元。 

快速幂：

//01序列 卡特兰数
#include<iostream>
using namespace std;
using ll = long long;
const ll mod = 1e9 + 7;//因为mod的数是质数可以用快速幂
//如果不是质数就用扩展欧几里得
ll qmi(ll a, ll k, ll p)
{ll res = 1;while (k){if (k & 1) res = res * a % p;a = a * a % p;k >>= 1;}return res;
}
//答案为C2n n /n + 1
int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll n; cin >> n;ll a = 2 * n, b = n, res = 1;for (ll i = a; i > a - b; --i) res = res * i % mod;for (ll i = 1; i <= b; ++i) res = res * qmi(i, mod - 2, mod) % mod;res = res * qmi(n + 1, mod - 2, mod) % mod;cout << res;return 0;
}

扩展欧几里得：

//01序列 扩展欧几里得
#include<iostream>
using namespace std;
using ll = long long;
const ll mod = 1e9 + 7;ll exgcd(ll a, ll b, ll& x, ll& y)
{if (!b){x = 1, y = 0;return a;}ll d = exgcd(b, a % b, y, x);y -= a / b * x % mod;return d;
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll n, x, y; cin >> n;ll a = 2 * n, b = n;ll res = 1;for (ll i = a; i > a - b; --i) res = res * i % mod;for (ll i = 1; i <= b; ++i){exgcd(i, mod, x, y);res = res * x % mod;}exgcd(n + 1, mod, x, y);res = (res * x % mod + mod) % mod;cout << res;return 0;
}