0.前言
好了那我们新的征程也即将开始,那么在此呢我也先啰嗦两句,本篇文章介绍数学基础的部分,因为个人精力有限我不可能没一字一句都讲得非常清楚明白,像矩阵乘法之类的一些基础知识我都是默认你会了(还不会的同学推荐去b站上一套课程:线性代数(mit的公开课版本)),就比如这篇文章的写作目的也只是带大家回顾一下后续我们敲代码需要使用的一些前置知识,当然我会在这些前置知识当中加入自己独特的见解,这也应该也是本个系列最有意思的地方。
1.向量
1.1什么是向量?
在数学中,向量是具有大小和方向的量。它可以表示为有序的数字集合,通常以列向量或行向量的形式表示。

上述图其实就能很好的概括我高中学过的一些基础知识。(我们高中学的模其实就是这里的长度,只是在图形学的领域我们会用两个绝对值来表示)
1.2平行四边形法则以及常用的一些表达

如上图所示,在我们在平面内进行基本的向量合成的时候,四边形法则无疑能很好的帮助我们。(这里向量与向量之间的最基本运算就不提了)
上图需要注意的是我们的采用矩阵的形式来指代了向量。
1.3点乘
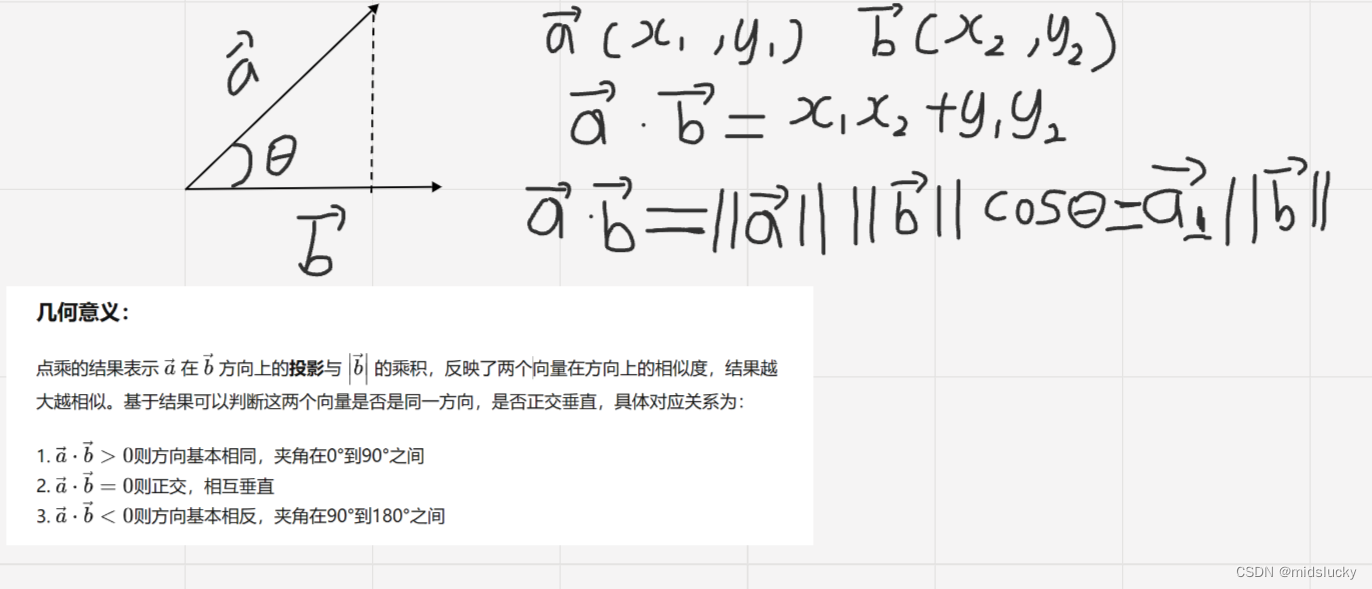

ok那基本上对点乘有了这些认知后就足够了。
1.4叉乘

基本上这副图就能囊括我所想要表达的一切,当然其公式的推导与证明过于繁杂就不在这里进行展开了。
简单的应用
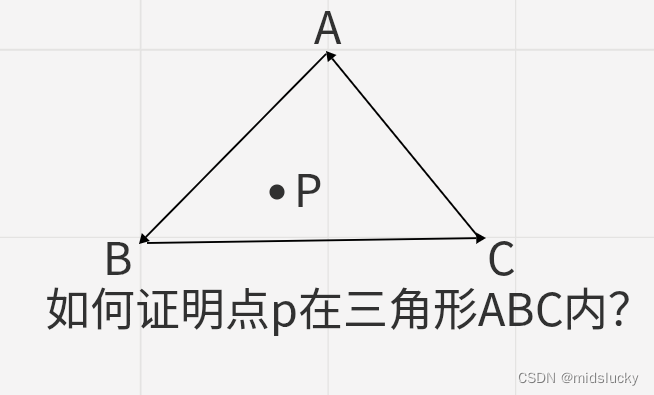
这个问题非常简单,只需要分别证明p分别在AB向量的右侧,在BC向量的左侧,AC向量的左侧(用叉乘得到的正负在加上右手螺旋法则即可)
(如果我此刻换成了以左手定则为标准会怎么样?这样的话我们上面定义的叉乘这一套就行不通了,因为上面的那一套都是以右手坐标系来定义的,如果定义成了左手坐标系,我们可以在右手所使用的计算规则上最后加个负号来得到左手坐标系下的运算值)
2.矩阵
2.1一些基础知识的回顾
(如果手上有资料的同学可以去翻看一下有关矩阵乘法的笔记)

当然有关这块内容这边也不做太多的解释只是带着大家回顾一下一些常用的,默认大家是有一定线代基础的。
2.2向量点乘与叉乘 和 矩阵乘法的一些关系