Introduction to Diffusion Models

生成模型
主要指的是无监督学习中的生成模型，在无监督学习中的主要任务是让机器学习给定的样本，然后生成一些新的东西出来。比如：给机器看一些图片，能够生成一些新的图片出来，给机器读一些诗，然后能够自己写诗出来。

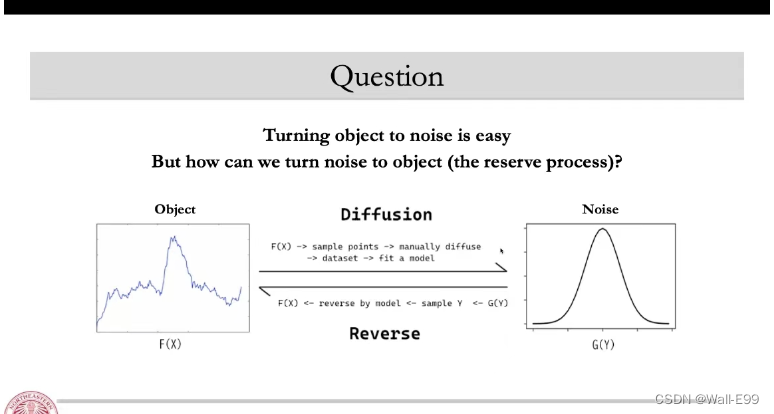
Forward Process

Forward Process I

Given $q\left(X_0\right),q\left(X_t\mid X_{t-1}\right)$, calculate $q\left(X_t\mid X_0\right)$

Forward step
$X_t=\sqrt{{\alpha }_t}{X}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t$, where ${ϵ}_t\sim N(0,I)$
Thus, $q\left(X_t\mid X_{t-1}\right)=N\left(\sqrt{{\alpha }_t}{X}_{t-1},\left(1-{\alpha }_t\right)I\right)$
（你保证alpha都是（0，1）的就行）

Forward Process II

$$\begin{array}{c}{X}_t=\sqrt{{\alpha }_t}{X}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t\\ =\sqrt{{\alpha }_t}\left(\sqrt{{\alpha }_{t-1}}{X}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{ϵ}_{t-1}\right)+\sqrt{1-{\alpha }_t}{ϵ}_t\\ =\sqrt{{\alpha }_t{\alpha }_{t-1}}{X}_{t-2}+\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{ϵ}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t\end{array}$$

Fact: The sum of two normal distributions is still a normal distribution

Therefore: $\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{ϵ}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t\sim N\left(0,\left({\alpha }_t-{\alpha }_t{\alpha }_{t-1}+1-{\alpha }_t\right)I\right)$
Let ${\alpha }_i=1-{\beta }_i$

Forward Process III

$$X_t=\sqrt{{\alpha }_t{\alpha }_{t-1}}{X}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}ϵ$$

After doing it for many times: $X_t=\sqrt{{\alpha }_t{\alpha }_{t-1}\dots {\alpha }_1}{X}_0+\sqrt{1-{\alpha }_t{\alpha }_{t-1}\dots {\alpha }_1}ϵ$

Therefore: $q\left(X_t\mid X_0\right)=N\left(\sqrt{\overline{{\alpha }_t}}{X}_0,\left(1-\overline{{\alpha }_t}\right)I\right)$, where $\overline{{\alpha }_t}={\alpha }_t{\alpha }_{t-1}\dots {\alpha }_1$

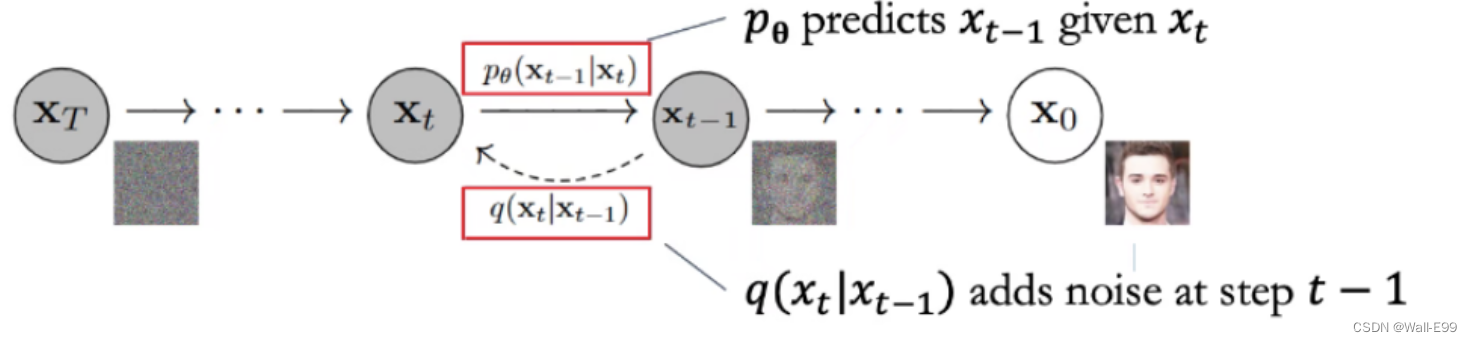
Reverse Process

Reverse Process I

Let us use Bayes Theorem
$$q\left(X_{t-1}\mid X_t\right)=q\left(X_{t-1}\mid X_t,X_0\right)=\frac{q\left(X_t\mid X_{t-1},X_0\right)q\left(X_{t-1}\mid X_0\right)}{q\left(X_t\mid X_0\right)}$$

Reverse Process II

We know these identities are true
$$\begin{array}{c}q\left(X_t\mid X_{t-1},X_0\right)\sim N\left(\sqrt{{\alpha }_t}{X}_{t-1},\left(1-{\alpha }_t\right)I\right)\\ q\left(X_t\mid X_0\right)=N\left(\sqrt{\overline{{\alpha }_t}}{X}_0,\left(1-\overline{{\alpha }_t}\right)I\right)\\ q\left(X_{t-1}\mid X_0\right)=N\left(\sqrt{\overline{{\alpha }_{t-1}}}{X}_0,\left(1-\overline{{\alpha }_{t-1}}\right)I\right)\end{array}$$

Reverse Process III

Let us apply these identities to the Bayes Theorem
$$\begin{array}{c}q\left(X_{t-1}\mid X_t\right)=\frac{q\left(X_t\mid X_{t-1},X_0\right)q\left(X_{t-1}\mid X_0\right)}{q\left(X_t\mid X_0\right)}\\ =\exp \left(-\frac{1}{2}\left(\frac{{\left(X_t-\sqrt{{\alpha }_t}{X}_{t-1}\right)}^2}{1-{\alpha }_t}+\frac{{\left(X_{t-1}-\sqrt{{\bar{\alpha }}_t}{X}_0\right)}^2}{1-{\bar{\alpha }}_{t-1}}-\frac{{\left(X_t-\sqrt{{\bar{\alpha }}_t}{X}_0\right)}^2}{1-{\bar{\alpha }}_t}\right)\right)\\ =\exp \left(-\frac{1}{2}\left(\left(\frac{{\alpha }_t}{1-{\alpha }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)X_{t-1}^2-\left(\frac{2\sqrt{{\alpha }_t}}{1-{\alpha }_t}{X}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{X}_0\right)X_{t-1}+C\left(X_t,X_0\right)\right)\right)\end{array}$$

Reverse Process IV

Find $\sigma$ and $\mu$ for the normal distribution
$$\begin{array}{rl}& \exp \left(-\frac{1}{2}\left(\left(\frac{{\alpha }_t}{1-{\alpha }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)X_{t-1}^2-\left(\frac{2\sqrt{{\alpha }_t}}{1-{\alpha }_t}{X}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{X}_0\right)X_{t-1}+C\left(X_t,X_0\right)\right)\right)\\ & \exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)=\exp \left(-\frac{1}{2}\left(\frac{1}{{\sigma }^2}{x}^2-\frac{2\mu }{{\sigma }^2}x+\frac{{\mu }^2}{{\sigma }^2}\right)\right)\\ & \end{array}$$

Reverse Process V

By matching the three terms, we get the solution for ${\mu }_t,{\sigma }_t$
$$\begin{array}{c}{\mu }_t=\frac{1}{\sqrt{{\alpha }_t}}\left(X_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t\right)\\ {\sigma }_t^2=\frac{\left(1-{\alpha }_t\right)\left(1-{\bar{\alpha }}_{t-1}\right)}{1-{\alpha }_t{\bar{\alpha }}_{t-1}}\end{array}$$
${\mu }_t,{\sigma }_t$是要我们解的东西
This is what we should use in the reserve process

Next: How to train the encoder ${ϵ}_t$

Loss Function

Want the reverse process ${\mathbf{p}}_{\theta }(\mathbf{X})$ as close as the forward process $\mathbf{q}(\mathbf{X})$
Use KL divergence as loss to match two distributions
$$D\left(q\left(X_0\right)\Vert p_{\theta }\left(X_0\right)\right)=\int q\left(X_0\right)\log \left(\frac{q\left(X_0\right)}{p_{\theta }\left(X_0\right)}\right)d{X}_0$$

常用tool：

The Evidence Lower Bound

• $\mathrm{ELBO}$ (Evidence Lower Bound)
• Let $p_{\theta }$ and $q_{\theta }$ be two distributions, we have:
  $$\ln p_{\theta }(x)\ge {\mathbb{E}}_{z\sim q_{\varphi }}\left[\ln \frac{p_{\theta }(x,z)}{q_{\varphi }(z)}\right].$$
• Step 1:
  $$L(\varphi ,\theta ;x):={\mathbb{E}}_{z\sim q_{\varphi }(\mid x)}\left[\ln \frac{p_{\theta }(x,z)}{q_{\varphi }(z\mid x)}\right].$$
• Step 2:
  $$\begin{array}{rl}L(\varphi ,\theta ;x)& ={\mathbb{E}}_{z\sim q_{\varphi }(\mid x)}\left[\ln p_{\theta }(x,z)\right]+H\left[q_{\varphi }(z\mid x)\right]\\ & =\ln p_{\theta }(x)-D_{KL}\left(q_{\varphi }(z\mid x)\Vert p_{\theta }(z\mid x)\right).\end{array}$$
• Conclusion (Many details skipped): Can derive a quadratic lower bound on KL divergence

ps 初步了解了一下clip

CLIP

clip初认识
它是一个 zero-shot 的视觉分类模型，预训练的模型在没有微调的情况下在下游任务上取得了很好的迁移效果。作者在30多个数据集上做了测试，涵盖了 OCR、视频中的动作检测、坐标定位等任务。
预训练网络的输入是文字与图片的配对，每一张图片都配有一小句解释性的文字。将文字和图片分别通过一个编码器，得到向量表示。这里的文本编码器就是 Transformer；而图片编码器既可以是 Resnet，也可以是 Vision transformer，作者对这两种结构都进行了考察。

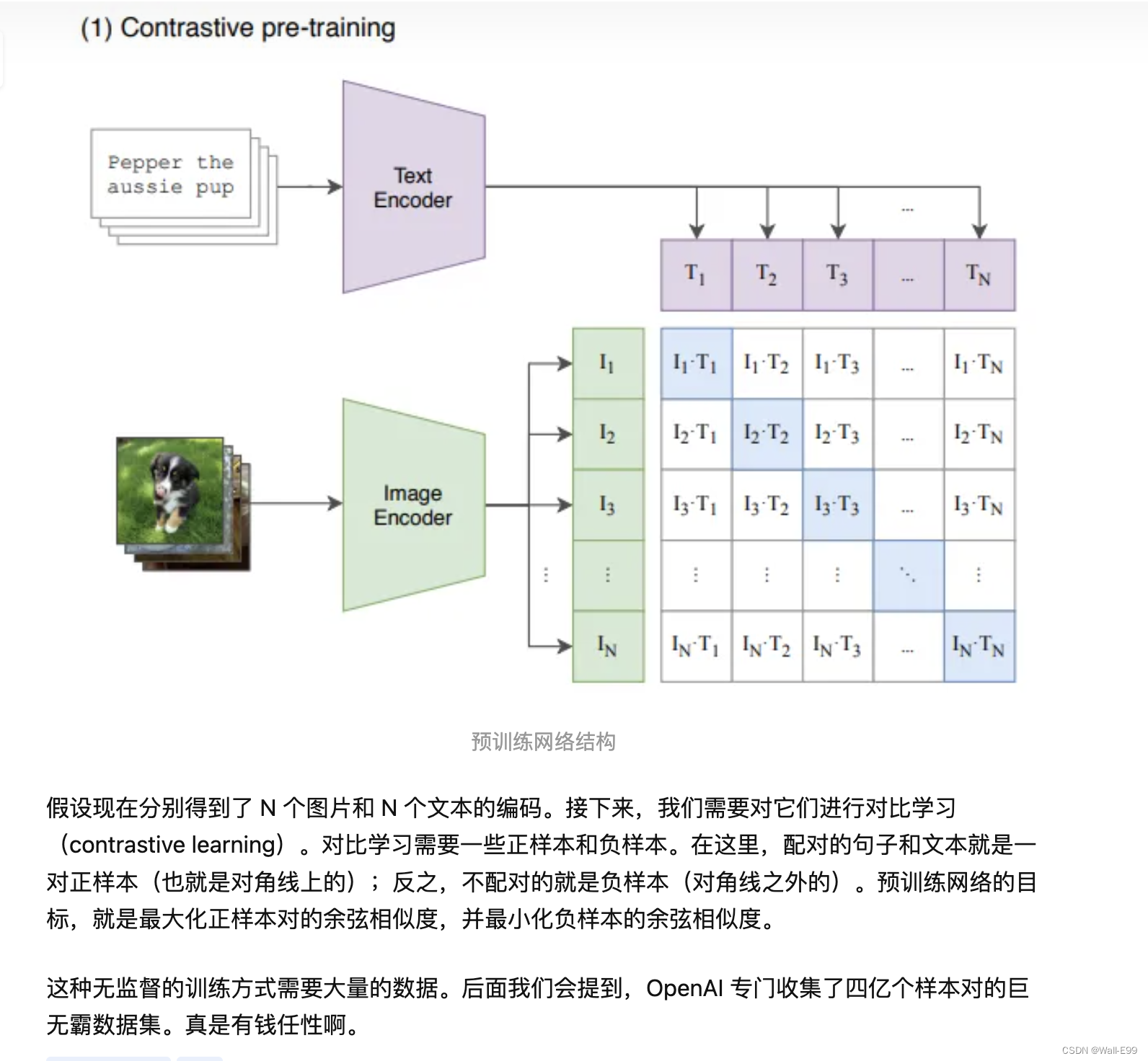
开源了预训练好的模型和 API，可以直接拿来做下游任务的推理：
https://github.com/openai/CLIP
https://openai.com/research/clip
一些可以试一试的项目：
https://github.com/yunhao-tech/Course_project/blob/master/Advanced%20Machine%20learning/Final%20project_CLIP.ipynb

当我们在谈论 Text-To-Image：Diffusion Model

背景
2022最卷的领域-文本生成图像
2021年1月，国际知名AI公司OpenAI公布了其首个文本生成图像模型DALL·E 。2021年12月底，OpenAI再次提出GLIDE模型，此模型能够生成比DALL·E更复杂、更丰富的图像。2022年4月，OpenAI又又又提出DALL·E 2，这次他们已经自信地表示“能够生成真实或者艺术图像”。仅一个月后，2022年5月，Google不甘落后发表其新模型Imagen，在写实性上击败DALL·E 2。

可以发现从2022年初开始，各种新模型如雨后春笋般冒出来，但其实它们背后都是一个模型范式：Diffusion Model 。下文我们就介绍下这个图像界的新贵，它在图像领域已经是比肩GAN的存在，或许其作用会进一步延伸到NLP，最终成为有一个通用模型范式。