数据结构——树状数组

文章目录

前言
问题引入
问题分析
树状数组
- `lowbit`
- 树状数组特性
- 初始化一个树状数组
- 更新操作
- 前缀和计算
- 区间查询
总结

前言

原题的连接
最近刷leetcode的每日一题的时候，遇到了一个区间查询的问题，使用了一种特殊的数据结构树状数组，学习完之后我不禁感叹这个数据结构设计的巧妙，下面是我的学习笔记。

问题引入

给你一个数组 nums ，请你完成两类查询。

其中一类查询要求更新数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（包含）的nums元素的和，其中 left <= right
实现 NumArray 类：

NumArray(int[] nums) 用整数数组 nums 初始化对象
void update(int index, int val) 将 nums[index] 的值更新为 val
int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（包含）的nums元素的和（即，nums[left] + nums[left + 1], …, nums[right]）

问题分析

这个问题我们可以总结为：

单点修改，就是一次只修改一个数（与之相对的是区间修改）
区间查询，查询某一个区间的和

我们如果用暴力的求解，在每次单点修改之后都需要重新计算一下区间的和，显然效率低下。
那我们如果使用前缀和数组进行求解，这样所有的区间和问题都可以转换成区间边界前缀和相减，但是每次单点修改之后，修改位之后的所有前缀和都需要修改。
通过上面的思考，我们发现每次单点修改，之后重新计算前缀和的成本太高了。那有没有一种方法能缩小这种由于单点更新导致的前缀和重新计算？

树状数组

我们先看一下树状数组长什么样子：
假设我们现在有一个数组a[]={1,5,7,4,3,2,1,6,7,3,0,4,9}
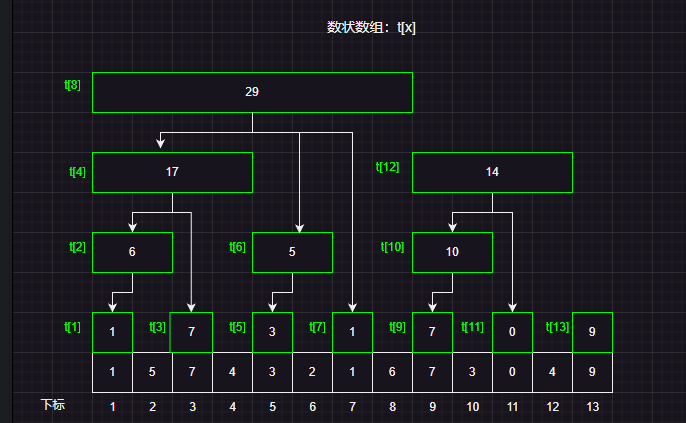
在这里插入图片描述

然后上图展示的就是一个树状数组，树状数组实际上一个数组，但是在逻辑结构上看做一个树形结构。其实和堆的底层结构是一样的。
数组的每个元素实际上代表的是某一个区间和，而树状数组设计巧妙的就是这个区间覆盖的长度的设计！
然后我们来逐一分析如何得到这么一颗树形结构

`lowbit`

什么一个数的lowbit ？
lowbit是最截取一个数二进制最低位的二进制1 到最末尾
例如数字6，他的二进制位为0110，取出它的lowbit位就变成了10转换成十进制就是2！
在这里插入图片描述
例如数字8，他的二进制为1000，取出它的lowbit位就变成了1000转换成十进制就是8

那么如何计算数字a的lowbit呢？
这个只需要 a&(-a)，就是a与上a的补码加1，补码加一使得最右边的1右边的所有位与a的二进制位均相同，而左边的位全部与a的二进制相反，这样一个操作直接能取出。

所以lowbit的函数就为：

	// 计算lowbit数值 int lowbit(int x) {return x & (-x);}

树状数组特性

理解了lowbit的概念之后我们在看这个树状数组：
我们对树状数组t[i]的定义是：原数组a在区间[i-lowbit(i),i]区间上的和（i的下标从1开始）
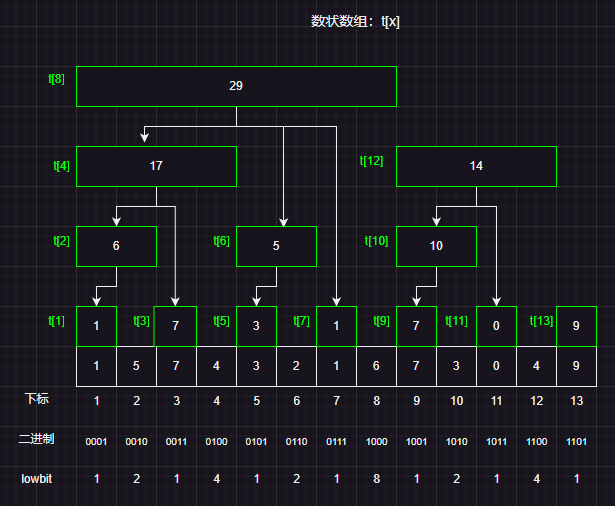
在这里插入图片描述

我们发现了树状数组实际上遵循以下规律：

t[i] 实际上代表的是一个a数组的某个区间的和，而这个区间长度正好是lowbit(i)
t[i]的父节点为t[i+lowbit(i)]，而父区间一定是包含子区间的，所以子区间发生更新之后，一定需要修改父区间
t[i]实际上就是数组在[i-lowbit(i)+1,i]这个区间上面的和

初始化一个树状数组

如果要初始化一个树状数组，我们需要定义两个数组，一个是用来保存原始的数组，一个用来保存树状数组：
初始化树状数组其实很简单：我们只需要牢记规律1，计算t[i]时，而为右边界通过规律1反推出左边界，就能计算出区间和

class TreeArray {private:vector<int> t;   // 树状数组vector<int> v;    // 原始数组// 计算lowbit数值 int lowbit(int x) {return x & (-x);}
public:// 初始化树状数组void Init(const vector<int>& x) {// 注意这里的v和t 下标都不是从0开始的，而是从1开始的v.resize(x.size() + 1);copy(x.begin(), x.end(), (++v.begin()));t.resize(x.size() + 1, 0);for (int i = 1; i <= x.size(); i++) {for (int j = i - lowbit(i) + 1; j <= i; j++) {t[i] += v[j];}}}
};

更新操作

更新操作也十分简单，由于更新之后需要修改某些区间和，这里牢记规律2，从子区间向上更新父区间，然后更新v和t数组

例如：下面我们需要修改下标为3的值，将它的值修改为4，那么区间和就需要增加1，然后将所有包含下标为3的区间都进行修改
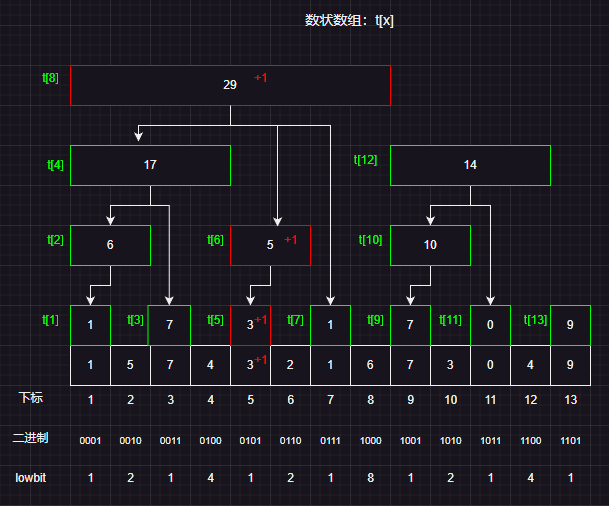
在这里插入图片描述


class TreeArray {private:vector<int> t;   // 树状数组vector<int> v;    // 原始数组// 计算lowbit数值 int lowbit(int x) {return x & (-x);}
public:// 初始化树状数组void Init(const vector<int>& x) {v.resize(x.size() + 1);copy(x.begin(), x.end(), (++v.begin()));t.resize(x.size() + 1, 0);for (int i = 1; i <= x.size(); i++) {for (int j = i - lowbit(i) + 1; j <= i; j++) {t[i] += v[j];}}}void Update(int index, int val) {// 传入的index是从0开始的，但是我们这里的树状数组下标是从1开始int dif = val - v[index + 1];  // 这里我们计算一个差值v[index + 1] = val;// 修改index的所有的父节点for (int i = index + 1; i < t.size(); i += lowbit(i)) {t[i] += dif;}}
};

前缀和计算

前缀和这个就更简单了，更具树状数组的定义

我们对树状数组t[i]的定义是：原数组a在区间[i-lowbit(i)+1,i]区间上的和（i的下标从1开始）

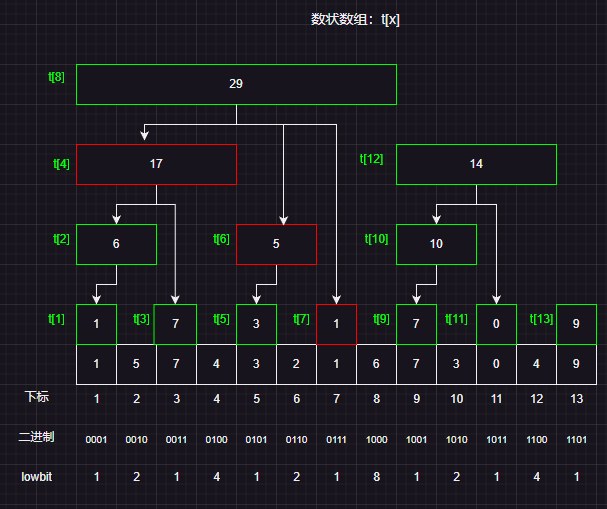
比方说我们要计算下标为7的前缀和，我们可以拆成t[7]+t[6]+t[4]，而我们发现7减去区间长度（lowbit(7)）就是t[6]，而t[6]减去区间长度t[4]…
这就是线段树的设计巧妙之处，把前缀和转换成多个树状数组元素相加！

在这里插入图片描述

class TreeArray {
private:vector<int> t;   // 树状数组vector<int> v;    // 原始数组// 计算lowbit数值 int lowbit(int x) {return x & (-x);}
public:// 初始化树状数组void Init(const vector<int>& x) {v.resize(x.size() + 1);copy(x.begin(), x.end(), (++v.begin()));t.resize(x.size() + 1, 0);for (int i = 1; i <= x.size(); i++) {for (int j = i - lowbit(i) + 1; j <= i; j++) {t[i] += v[j];}}}void Update(int index, int val) {// 传入的index是从0开始的，但是我们这里的树状数组下标是从1开始int dif = val - v[index + 1];v[index + 1] = val;// 修改index的所有的父节点for (int i = index + 1; i < t.size(); i += lowbit(i)) {t[i] += dif;}}// 算出index的前缀和int GetPrefixSum(int index) {int sum = 0;for (int i = index + 1; i > 0; i -= lowbit(i)) {sum += t[i];}return sum;}
};

区间查询

我们直接把区间查询转换成前缀和相减！

class TreeArray {private:vector<int> t;   // 树状数组vector<int> v;    // 原始数组// 计算lowbit数值 int lowbit(int x) {return x & (-x);}
public:// 初始化树状数组void Init(const vector<int>& x) {v.resize(x.size() + 1);copy(x.begin(), x.end(), (++v.begin()));t.resize(x.size() + 1, 0);for (int i = 1; i <= x.size(); i++) {for (int j = i - lowbit(i) + 1; j <= i; j++) {t[i] += v[j];}}}void Update(int index, int val) {// 传入的index是从0开始的，但是我们这里的树状数组下标是从1开始int dif = val - v[index + 1];v[index + 1] = val;// 修改index的所有的父节点for (int i = index + 1; i < t.size(); i += lowbit(i)) {t[i] += dif;}}// 算出index的前缀和int GetPrefixSum(int index) {int sum = 0;for (int i = index + 1; i > 0; i -= lowbit(i)) {sum += t[i];}return sum;}// 区间查询int Select(int begin, int end) {return GetPrefixSum(end) - GetPrefixSum(begin - 1);}
};