算法通关村——数字中的统计、溢出、进制转换处理模板

数字与数学基础问题

1、数字统计

1.1、符号统计

LeetCode1822. 给定一个数组，求所有元素的乘积的符号，如果最终答案是负的返回-1，如果最终答案是正的返回1，如果答案是0返回0.

这题其实只用看数组中0和负数的个数就好了，数组中有0的话，最后的结果肯定是0，数组中负数的个数是奇数的话，最终结果就是负的，偶数个的话结果就是正的。代码如下：

public int arraySign(int[] nums) {int prod = 1;for (int i = 0; i < nums.length; i++) {if (nums[i] == 0) {return 0;} else if (nums[i] < 0) {//直接交替就好了，很好的处理技巧prod = -prod;}}return prod;
}

1.2、阶乘结果中末尾0的个数

设计一个算法，算出n阶乘后有多少个尾随0。

这题如果硬算的话肯定会花费很多时间，我们可以换个角度思考，如果一个数的末尾有0，肯定是乘过10的，而10是由 2 * 5得来的，所以只用统计2和5一起出现多少对，不过因为2出现的次数一定大于5出现的次数，因此我们只需要统计5出现的次数就好了。在统计的过程中，我们只需要统计5、10、15、…… $5^n$ 这样5的整数倍就好了，最后累加起来，就是多少个0。代码如下：

public int trailingZeroes(int n) {int cnt = 0;for (long num = 5; n / num > 0; num *= 5) {cnt += n / num;}return cnt;
}

这里num * 5 是因为 n / num 首先计算的是从1到n数中包含1个5的个数，比如1 * 5 = 5，2 * 5 = 10，然后计算的是包含2个5的个数，比如5 * 5 = 25，5 * 5 * 2 = 50，以此类推，加起来就是最终结果中含5的个数。

2、溢出问题

2.1、整数反转

LeetCode7. 给你一个32位的有符号整数x，返回将x中的数字部分反转后的结果。如果反转后整数超过32位的有符号整数的范围[-2^31 , 2^31 - 1]，就返回0.假设环境不允许存储64位整数（有符号或无符号）。

这题需要考虑溢出的问题，比如1147483649这个数字，它是小于最大的32位整数2147483647的，但是将这个数字反转过来后就变成了9463847411，这就比最大的32位整数还要大了，这样的数字是没法存到int中的，所以就溢出了。

取得一个数中的各个位上的数字很简单，循环取模即可，例如取得12345的各个数位上的数字，首先将12345 % 10 = 5，就得到个位数上的数字5，然后将12345 / 10 = 1234，这样再继续模10就好了，如下图所示：

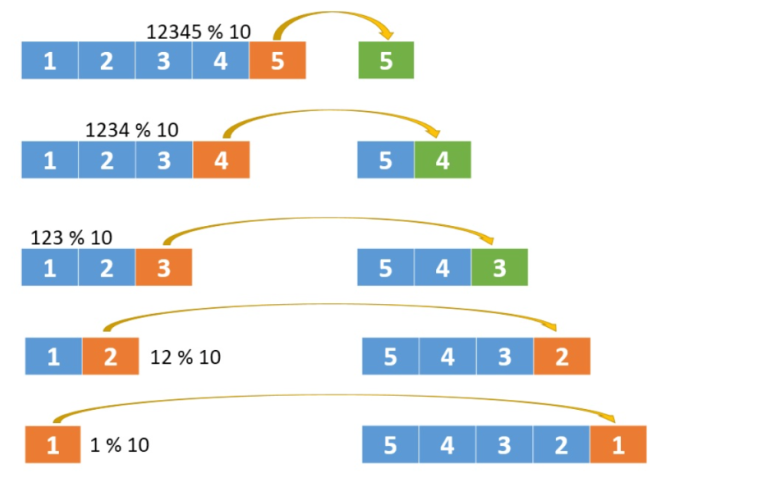
这是正数的情况，如果再考虑负数的话，可以将循环设置为while(x != 0)。因为无论是正数还是负数，按照上面不断的/10操作，最后都会变为0，所以判断终止条件就是 != 0。

再就是怎么去处理溢出的问题，我们需要从倒数第二位开始判断是否溢出，因为如果直接比较最终的结果的话，像上面所讲到的，一旦数溢出的话int是存不下的，所以得提前判断。而32位最大整数MAX=2147483647，它的倒数第二位是4，所以就要分析结果的倒数第二位和4的大小关系，如下所示：

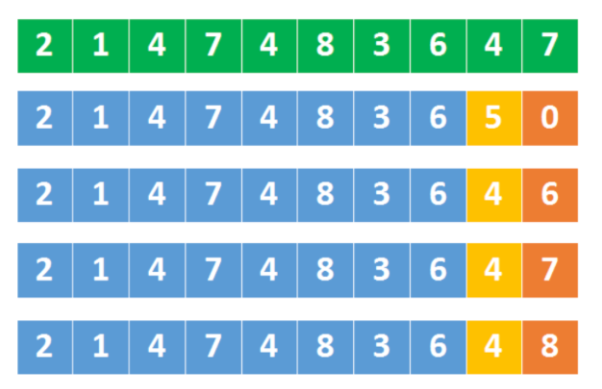
如果res > 214748364，那最后一位要接上的数就不用看了，肯定溢出了
如果res = 214748364，就需要跟最大数的最后一个数字相比，如果比7大，那就说明溢出了
如果res < 214748364，继续处理即可，不会溢出

对于负数同理，代码如下：

public int reverse(int x) {int res = 0;while(x != 0) {//获得末尾数字int temp = x % 10;//判断是否大于最大的32位整数if (res > Integer.MAX / 10 || (res == Integer.MAX / 10 && temp > 7)) {return 0;}//判断是否小于最小的32位整数if (res < Integer.MIN / 10 || (res == Integer.MIN / 10 && temp < -8)) {return 0;}res = res * 10 + temp;x /= 10;}return res;
}

3、进制专题

3.1、进制转换

给定一个十进制数M，以及需要转换的进制数N，将十进制数M转化位N进制数。M是32位整数，2<=N<=16.

对于这个问题，需要处理以下的几个点：

超过进制最大范围后需要映射到其他进制，比如用ABCDEF去表示数
需要对结果进行转置
需要判断符号

用以下三个措施可以比较方便的去处理这个问题：

定义大小位16的数组F，保存的是2到16的各个进制的值对应的标记，这样赋值时只计算下标，不必考虑不同进制的转换关系
使用StringBuffer完成数组转置等功能
通过一个flag来判断正数还是负数

//要考虑到余数>9的情况，2 <= N <= 16
public static final String[] F = {"0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "A", "B", "C", "D", "E", "F"};//将十进制数M转化位N进制数
public String convert(int M, int N) {if (M < 0) {flag = true;M * -1;}StringBuffer sb = new StringBuffer();int temp;while(M != 0){temp = M % N;sb.append(F[temp]);M = M / N;}sb.reverse();return (flag ? "-" : "") + sb.toString();
}