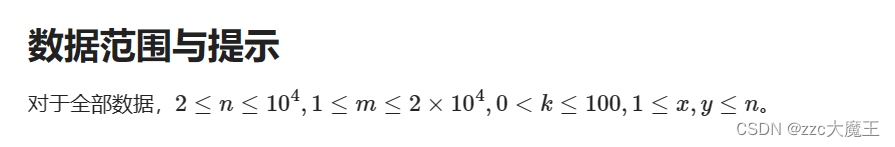
---

分析

根据数据范围分析一下复杂度，Floyd和dj算法都必爆。

发现题目说的是树，还是边还是双向的（树本身就是无向的，连通无回路的无向图叫做无向树，简称树。如果题目说了树，那么默认边就是双向的），也没指明根节点，那么就是无根树，任选一个节点当根节点。

思路

是树的话就简单了，任意两点之间的最短距离很容易想到最近公共祖先，x到LCA的距离加上y到LCA的距离就是最短距离。

考虑在LCA预处理的dfs里面加上dis数组维护每个节点到根节点的距离。

那么x，y两点的最短距离就是dis[x]+dis[y]-2*dis[lca(x,y)]

AC代码

#include <bits/stdc++.h>
using namespace std;inline int read(){int x=0;char c=getchar();while(c<48 or c>57)c=getchar();while(c>=48 and c<=57)x=(x<<3)+(x<<1)+(c xor 48),c=getchar();return x;
}using pii=pair<int,int>;
const int N=1e4+5;
int n,m,lg[N],d[N],f[N][15],dis[N];
vector<pii>e[N];
bitset<N>vis;void dfs(int now,int fa){if(vis[now])return;//使用vector别忘了加vis，不然会访问父节点vis[now]=true;f[now][0]=fa;d[now]=d[fa]+1;for(int i=1;i<=lg[d[now]];++i)f[now][i]=f[f[now][i-1]][i-1];for(auto i:e[now]){if(!vis[i.second]){dis[i.second]=dis[now]+i.first;dfs(i.second,now);}}
}
int lca(int x,int y){if(d[x]<d[y])swap(x,y);while(d[x]>d[y])x=f[x][lg[d[x]-d[y]]-1];if(x==y)return x;for(int i=lg[d[x]];i>=0;--i)if(f[x][i]!=f[y][i]){x=f[x][i];y=f[y][i];}return f[x][0];
}int main(){ios::sync_with_stdio(false);n=read(),m=read();for(int i=1,x,y,k;i<=n-1;++i){x=read(),y=read(),k=read();e[x].push_back({k,y});e[y].push_back({k,x});}for(int i=1;i<=n;++i)lg[i]=log(i)/log(2)+1;dfs(1,1);for(int i=1,x,y;i<=m;++i){x=read(),y=read();cout<<dis[x]+dis[y]-2*dis[lca(x,y)]<<endl;}return 0;
}

倍增LCA代码细节有点多，被卡了两发。

1. d[x]>d[y]跳到同一深度之后先判断是不是到一个点了，是就直接返回。

2. 往上跳的时候是f[x][lg[d[x]-d[y]]-1]，因为预处理的时候lg加了1