文章目录
- 🥦引言:
- 🥦什么是堆
- 🥦大顶堆与小顶堆
- 🧄大顶堆(Max Heap)
- 🧄小顶堆(Min Heap)
- 🥦堆的表示
- 🧄数组表示:
- 🧄树表示:
- 🥦堆的操作
- 🧄堆化操作
- 🧄插入操作
- 🧄删除根节点操作
- 🧄堆的创建
- 🥦堆的应用
- 🧄优先队列
- 🧄堆排序
- 🧄辅助数据结构
- 🥦堆的复杂度分析
- 🥦结论
- 🥦参考文献
🥦引言:
在计算机科学中,数据结构和算法是构建复杂软件系统的基石。堆作为一种经典的数据结构,具有广泛的应用和重要的算法基础。本文将深入解析堆的原理、性质和常见的操作,帮助读者更好地理解和应用堆。
🥦什么是堆
堆是一种特殊的数据结构,属于树的一种表现形式。堆具有以下两个主要特征:
-
堆是一个完全二叉树(或近似完全二叉树):堆中的所有层次都被填满,最后一层从左到右填入节点。
-
堆具有堆序性:对于最小堆来说,父节点的值始终小于或等于其子节点的值;对于最大堆来说,父节点的值始终大于或等于其子节点的值。
-
在堆中,每个节点的值都取决于其子节点的值:对于最小堆来说,父节点的值不大于任何子节点的值;对于最大堆来说,父节点的值不小于任何子节点的值。
🥦大顶堆与小顶堆
对于堆来说,可以根据节点的性质分为两种类型:大顶堆(Max Heap)和小顶堆(Min Heap)。
🧄大顶堆(Max Heap)
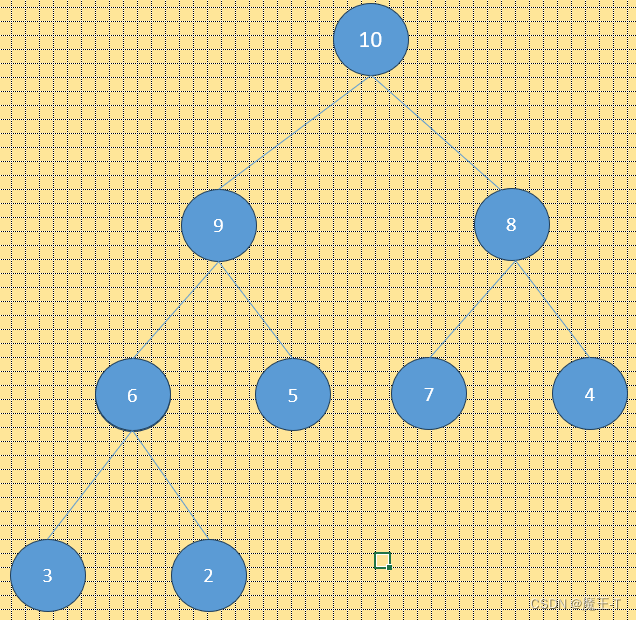
在大顶堆中,父节点的值大于或等于其子节点的值。也就是说,大顶堆的根节点是堆中的最大值。对于任意节点i,其子节点的值必须小于或等于节点i的值。大顶堆常用于获取最大值或进行部分排序。
结构表示如下:
🧄小顶堆(Min Heap)
在小顶堆中,父节点的值小于或等于其子节点的值。也就是说,小顶堆的根节点是堆中的最小值。对于任意节点i,其子节点的值必须大于或等于节点i的值。小顶堆常用于获取最小值或进行部分排序。
结构表示如下:

无论是大顶堆还是小顶堆,堆的逻辑结构和操作都是相同的。唯一的区别是节点的值大小和根节点的值。
在实际应用中,大顶堆和小顶堆都有各自的用途。例如,在优先队列中,可以使用大顶堆来实现,以便快速获取优先级最高的元素。而在进行部分排序时,可以使用小顶堆来实现,以方便获取最小的k个元素。
无论是大顶堆还是小顶堆,它们都是一种非常重要的数据结构,在算法和数据处理中有广泛的应用。了解堆的性质和操作,可以帮助我们更好地理解和应用这两种堆。
🥦堆的表示
堆可以使用数组或树来表示。下面分别介绍这两种表示方法:
🧄数组表示:
-
在数组表示中,堆的元素按照完全二叉树的形式存储在一个数组中。
-
堆的根节点存储在数组的索引位置0处。
-
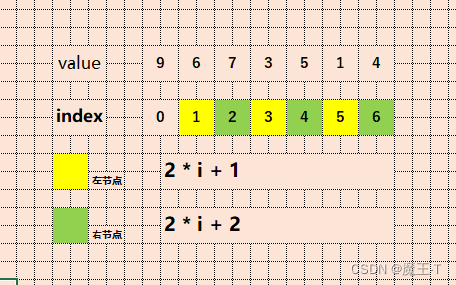
对于索引为i的节点,其左子节点的索引为2i + 1,右子节点的索引为2i + 2。
-
通过数组的索引关系,可以方便地在堆的插入、删除等操作中定位到对应的节点。
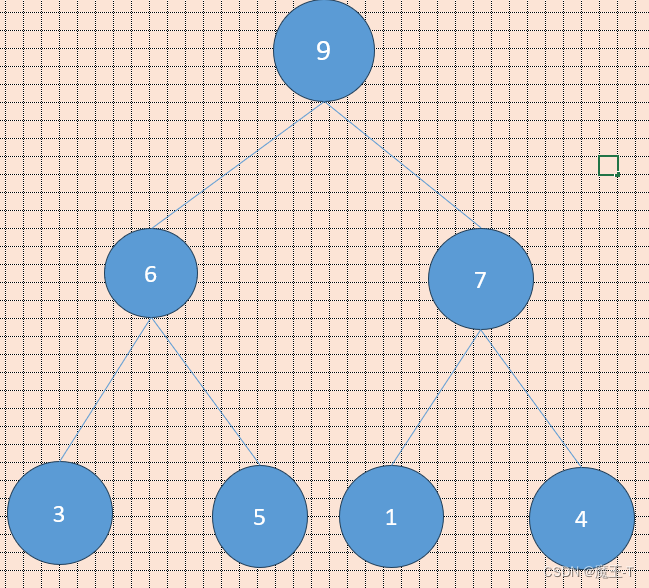
例如,对于一个大顶堆(Max Heap)的数组表示:heap = [9, 6, 7, 3, 5, 1, 4],可以构建如下的堆结构:
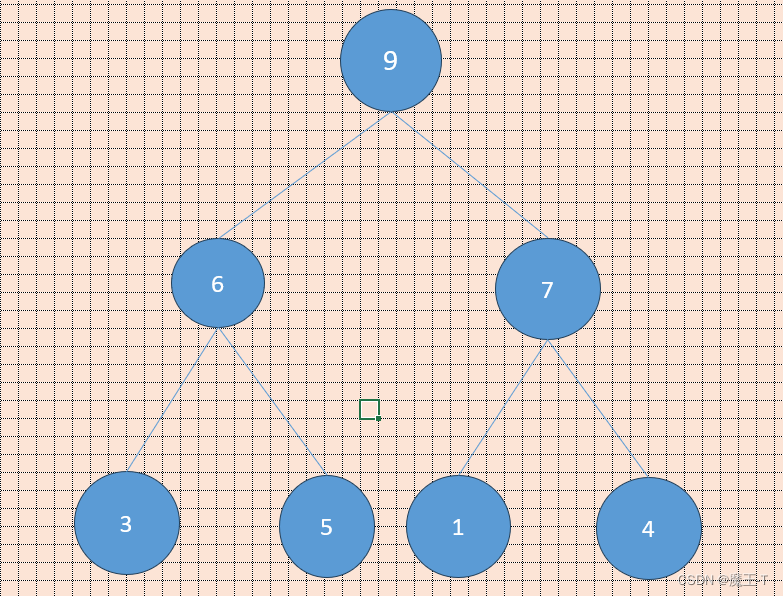
数组表示:
🧄树表示:
-
在树表示中,堆可以使用二叉树进行表示。
-
堆的根节点是二叉树的根节点。
-
每个节点最多有两个子节点,并且子节点与父节点之间有特定的大小关系(对于大顶堆是大于等于,对于小顶堆是小于等于)。
-
通过指针或引用,可以方便地在堆的插入、删除等操作中定位到对应的节点。
-
例如,对于一个大顶堆(Max Heap)的树表示:
🥦堆的操作
🧄堆化操作
首先引入堆化的概念, 当我们向一个已经是堆的数据结构(如数组或二叉堆)中插入一个新元素时,需要进行插入操作,并保持堆的性质。这个过程可以称为"堆插入"。堆插入的一般步骤如下:
将新元素插入到堆的最后一个位置(或数组的末尾)。
向上调整(也称为上浮)新插入的元素,直到它在堆中找到合适的位置并满足堆的性质。
具体来说,对于大顶堆(Max Heap)的情况,堆插入的过程如下:
将新元素插入到堆的最后一个位置。
与其父节点进行比较,如果新元素的值大于父节点的值,则交换它们的位置。
重复上述步骤,直到新元素找到了合适的位置并满足堆的性质。
类似地,对于小顶堆(Min Heap)的情况,堆插入的过程如下:
将新元素插入到堆的最后一个位置。
与其父节点进行比较,如果新元素的值小于父节点的值,则交换它们的位置。
重复上述步骤,直到新元素找到了合适的位置并满足堆的性质。
通过堆插入操作,可以在保持堆的性质下有效地将新元素插入到堆中,并且时间复杂度为O(log n),其中n表示堆的大小。插入完成后,堆将继续保持堆的性质。
🧄插入操作
向堆中插入一个新节点。通常,插入操作首先将新节点添加到堆的末尾,然后通过向上调整(上滤)操作来恢复堆的堆序性。
示例:
-
初始状态

-
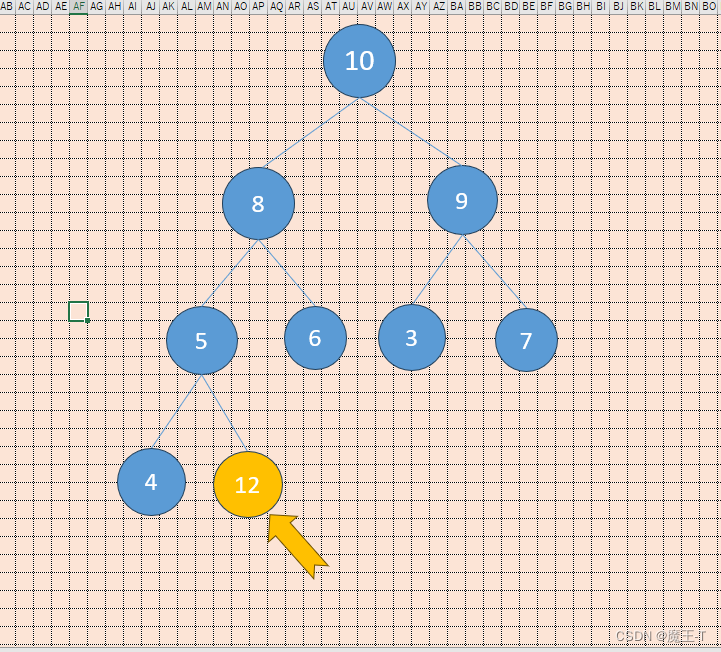
插入元素12
插入12后,需要将其与父节点5进行比较,因为12大于5,所以交换它们的位置。
-
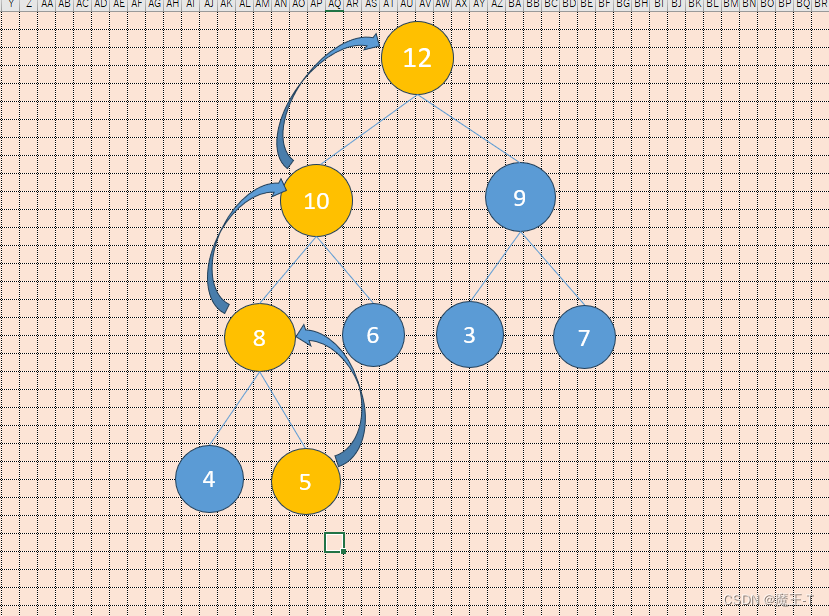
插入12后,需要将其与父节点5进行比较,因为12大于5,所以交换它们的位置。然后,还需要将12与其父节点8进行比较,因为12大于8,所以交换它们的位置。最后,还需要将12与其父节点10进行比较,因为12大于10,所以交换它们的位置。
代码示例
def heapify_up(heap, index):parent_index = (index - 1) // 2while parent_index >= 0 and heap[index] > heap[parent_index]:heap[index], heap[parent_index] = heap[parent_index], heap[index]index = parent_indexparent_index = (index - 1) // 2def insert_into_heap(heap, new_item):heap.append(new_item)heapify_up(heap, len(heap) - 1)# 示例使用:
heap = [10,8,7,5,6,3,4]
print("原始堆:", heap)insert_into_heap(heap, 9)
print("插入后的堆:", heap)
🧄删除根节点操作
将堆中的根节点删除。通常,删除根节点后,将堆中最后一个节点移到根位置,然后通过向下调整(下滤)操作来恢复堆的堆序性。
下面是一个示例的大顶堆删除操作的结构图:
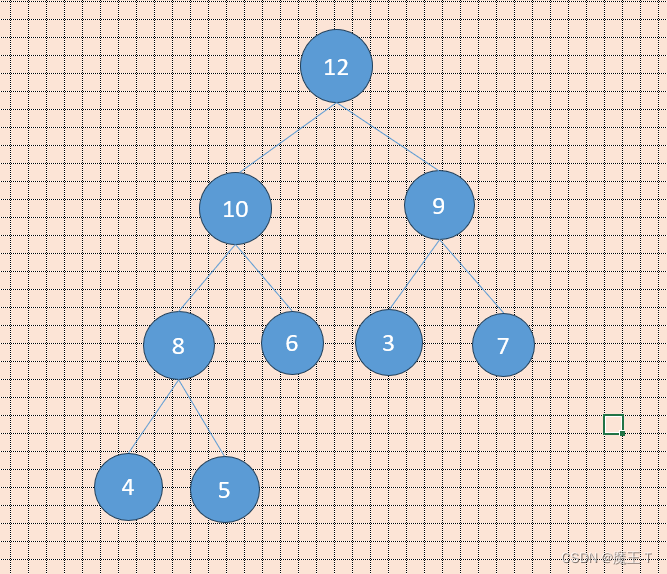
- 初始状态:
- 删除堆顶元素12:
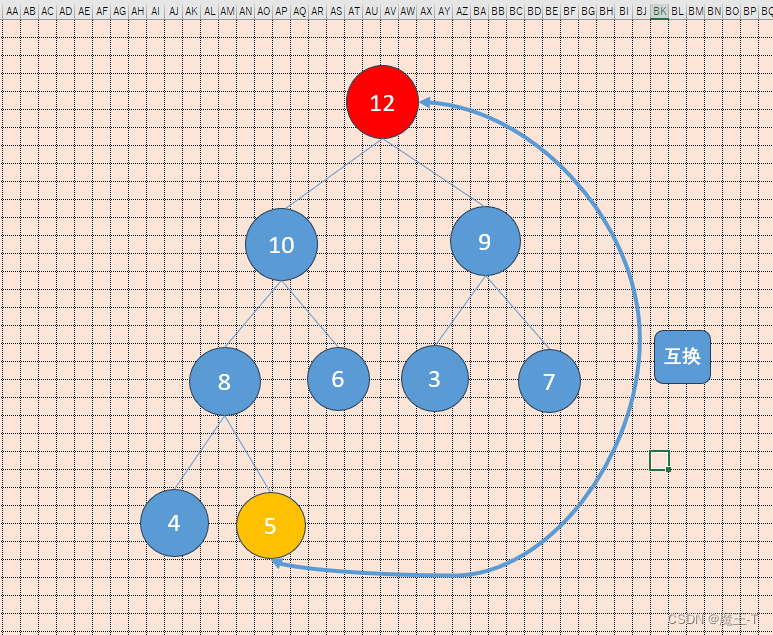
删除堆顶元素时,需要将最后一个元素5替换到堆顶,然后通过向下调整操作,将其移动到合适的位置,并保持大顶堆的性质。
- 向下调整操作:

在向下调整的过程中,将当前节点与其子节点进行比较,如果子节点的值较大,则将当前节点与较大的子节点交换位置。继续以上比较和交换的步骤,直到当前节点不再有子节点或者当前节点的值大于等于其子节点的值,保持大顶堆的性质。
- 最终结果:
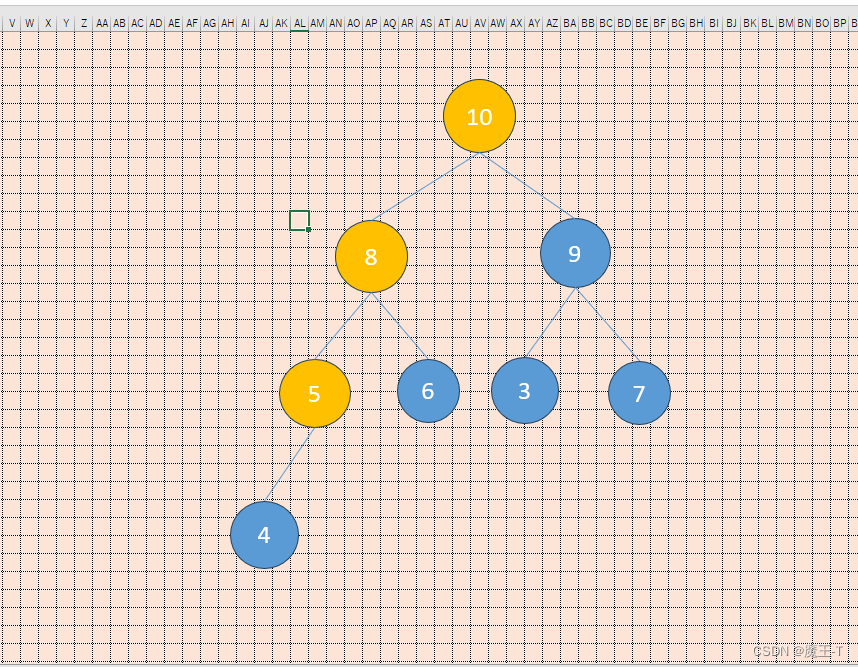
在删除堆顶元素的过程中,需要进行多次比较和交换,并通过向下调整操作将新的堆顶元素移动到正确的位置,同时保持大顶堆的性质。以上是一个简单的示例,实际操作中可能还需要考虑边界情况和特殊情况的处理。
下面是一个示例的 Python 代码,展示了如何执行堆的删除操作:
import heapq# 创建一个堆
heap = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5]# 将列表转换为堆
heapq.heapify(heap)# 删除堆顶元素
root = heapq.heappop(heap)print("删除的堆顶元素:", root)
print("删除后的堆:", heap)
输出如下:
删除的堆顶元素: 1
删除后的堆: [2, 3, 4, 3, 5, 9, 5, 6, 5]
在上述代码中,使用了 heapq 模块提供的函数来执行堆操作。heapify 函数将普通列表转换为堆,heappop 函数用于删除堆顶元素,并返回被删除的元素。最后,打印删除的堆顶元素和删除后的堆。
🧄堆的创建
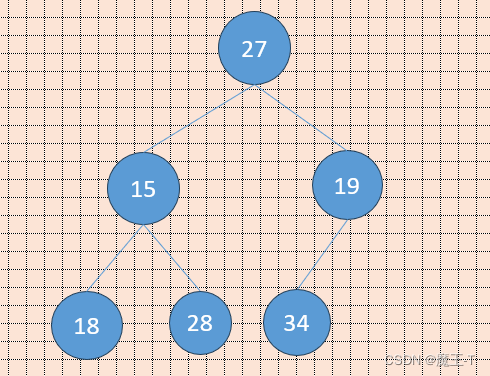
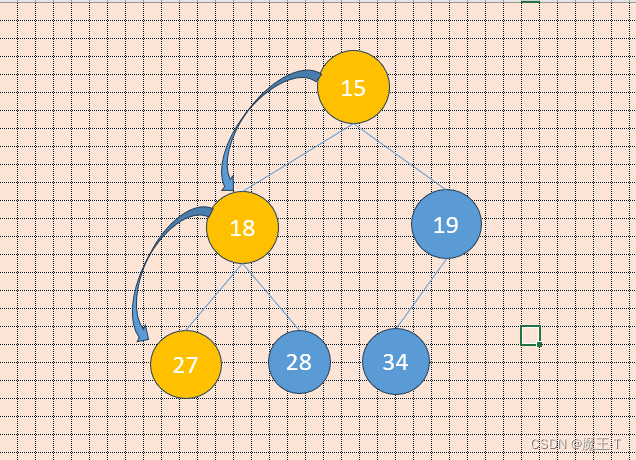
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
int array[] = {27,15,19,18,28,34};
🥦堆的应用
🧄优先队列
使用堆来实现优先队列,可以快速找到最大或最小的元素,并在一系列数据中动态调整优先级。
🧄堆排序
堆排序是一种高效的排序算法,利用堆的性质进行排序操作。
🧄辅助数据结构
堆在其他算法和数据结构中的实现中起到辅助作用,如图的最短路径算法中使用的Dijkstra算法。
🥦堆的复杂度分析
堆的插入和删除操作的时间复杂度均为O(log n),其中n为堆中元素的数量。堆化操作的时间复杂度为O(n)。
🥦结论
堆作为一种重要的数据结构,在计算机科学中广泛应用。通过深入理解堆的原理、性质和操作,我们能够更好地应用堆解决实际问题。堆不仅作为优先队列和排序算法的基础,还在各种算法和系统中发挥着重要的作用。熟练掌握堆的概念和操作,将极大地提高算法设计和实现的能力。
🥦参考文献
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to algorithms. MIT press.
🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄🍄
🏫博客主页:魔王-T
🏯系列专栏:结构算法
🥝大鹏一日同风起 扶摇直上九万里
❤️感谢大家点赞👍收藏⭐评论✍️
END






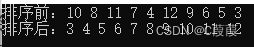

![[vxe-table] expandAll:true 当table数据更新后无法展开,只有第一次能展开才能生效的问题](https://img-blog.csdnimg.cn/09fc97e1c7414eedb26f6612e35dc750.png)