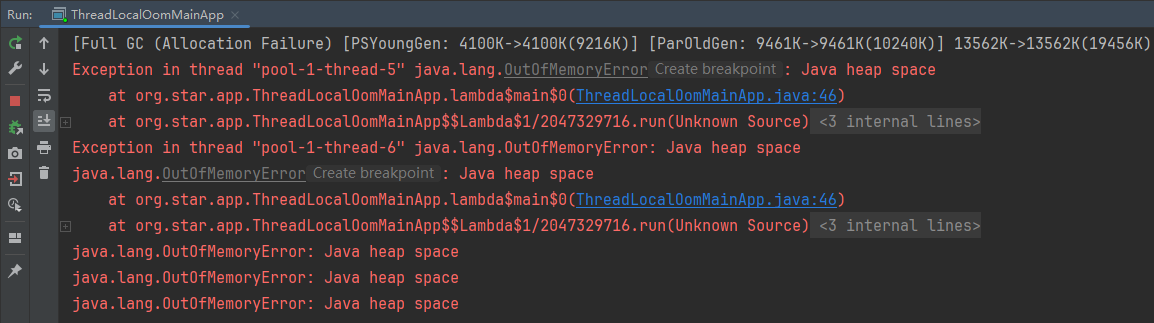
我们知道算法的效率分为时间效率和空间效率,接下来我们就对这两者进行讨论。
一.时间复杂度.
又被称为时间效率,主要反映一个算法的运行速度。
定义:计算机算法中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间,一个算法所发挥的时间与其中语句的执行次数成正比,算法中的基本操作的执行次数为算法的时间复杂度。
下面我们就通过具体实例来慢慢学会它!
例一:
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void Func1(int N)
{int count = 0;for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){++count;}}for (int k = 0; k < 2 * N; k++){++count;}int M = 10;while (M){++count;}printf("%d\n", count);}
int main()
{int N = 0;scanf("%d", &N);Func1(N);return 0;
}看这个代码,问题来了,请问它一共循环多少次?
结果为:N*N+N*2+10
接下来我们就可以看看时间复杂度了。
首先,时间复杂度是一个估算,是看表达式中对其影响最大的一项(当N趋近无穷大
时),所以对于上面这个表达式,N*N对时间复杂度影响最大,就取它。
接下来我们用大O渐进法来表示:
对于上表达式:O(N^2)
understand?
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数
2、在修改后的运行次数函数中,只保留最高阶项
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:O(N^2)
接下来我们一题来分析上述情况:
例二:
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; k++){++count;}int M = 10;while (M){++count;}printf("%d\n", count);}
int main()
{int N = 0;scanf("%d", &N);Func2(N);return 0;
}
求其时间复杂度:
首先循环次数:2*N+10
时间复杂度为:O(N)-----对于上面规律三的运用
例三:
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void Func3(int N,int M)
{int count = 0;for (int i = 0; i < N; i++){count++;}for (int j = 0; j < M; j++){count++;}printf("%d\n", count);
}
int main()
{int N = 0;int M = 0;scanf("%d %d", &N,&M);Func3(N,M);return 0;
}求其时间复杂度?
循环次数:M+N
时间复杂度:我们发现这题要分类讨论
1.当M与N大小差不对时,O(M) ,O(N)都行
2.当M远大于N时,O(M)
3.当N远大于M时,O(N)
例四:
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void Func3(int N)
{int count = 0;for (int i = 0; i < 100; i++){count++;}printf("%d\n", count);
}
int main()
{int N = 0;scanf("%d %d", &N);Func3(N);return 0;
}求其时间复杂度:
循环次数:100
时间复杂度:O(1)
用常数1取代运行时间中的所有加法常数
满足公式1
例五:
const char* Func5(char* a, char b)
{while (*a != '\0'){if (*a == b){return a;a++;}}return NULL;
}求时间复杂度?
有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
评均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况: N次找到
平均情况: N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
对于这题,同理;由于不知道会循环多少次,所以我们按最坏情况来写,即O(N)
例六:
void Bubblesort(int* a, int n)
{for (int i = 0; i < n-1; i++){for (int j = 0; j < n-1 - i; j++){if (*(a + j) > *(a + j + 1)){int tmp = *(a + j);*(a + j) = *(a + j + 1);*(a + j + 1) = tmp;}}}
}求其时间复杂度?
循环次数:第一趟:N-1
第二趟:N-2
……
第N-1趟:1
所以总共: ( N*(N+N-1))/2
时间复杂度:O(N^2)
例七:
int Binarysearch(int* arr, int n, int x)
{int left = 0;int right = n;while (left < right){int mid = (left + right) / 2;if (x > arr[mid]){left = mid + 1;}if (x < arr[mid]){right = mid - 1;}if (x== arr[mid]){return mid;}}return -1;
}求时间复杂度?
循环次数:
对于该题又要分情况讨论了
1,可能一次就可以-----最好情况O(1)
2.最坏情况:
要X次:2^X=N => log2N(2是底数)
时间复杂度:0(logN)
注意:算法的复杂度计算,喜欢省略简写成logN,因为很多地方不好写底数,有些书本,或者网上资料会写成O (lgN),严格来说这个不对的
例题八:
long long int Factorial(int n)
{return n < 2 ? n : Factorial(n - 1) * n;
}求时间复杂度?
循环次数:递归了N次
时间复杂度:0(N)
常见时间复杂度分析:
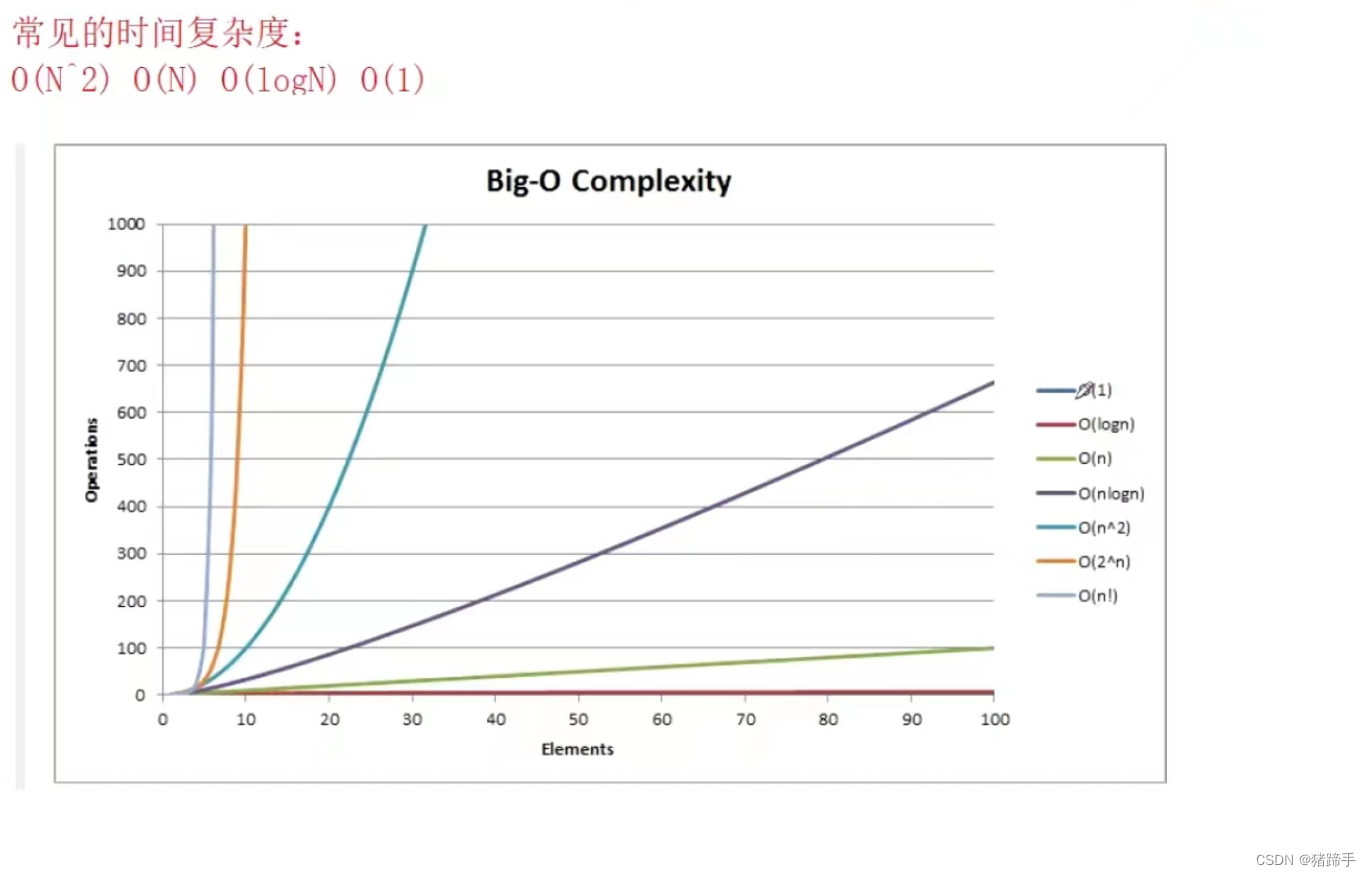
通过对比我们发现:
不同的时间复杂度是存在非常大的差距的,我们能实现越小越好。
二.空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
我们还是通过例题来比较:
例一:
void Bubblesort(int* arr, int n)
{for (int i = 0; i < n-1; i++){for (int j = 0; j < n - 1 - i; j++){if (arr[j] > arr[j + 1]){int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;}}}
}首先:在这里,我们要明白时间是累计的,空间是不累计,所以,对于这题,我们发现变量只有3个(参数不算),大O渐进法表示为:O(1)
注意:该循环走了N次,重复利用的是一个空间
例二:
long long int Factorial(int n)
{return n < 2 ? n : Factorial(n - 1) * n;
}算空间复杂度?
递归只在整体返回时才消除栈帧,递归调用了N层,每次调用建立一个栈帧,每个栈帧使用了常数个空间 ,所以空间复杂度为:O(1)
最后,诸君共勉!!!