首先MySQL的数据**(索引+记录)**是存在磁盘里的,磁盘读取非常慢,所以要尽可能减少磁盘操作,因此我们需要更好的利用索引。
首先索引按顺序排列了数据,那么很显然最好的查找方式是二分查找,数组自然是一个初步的想法,但对于插入删除而言,数组开销太大,那么有什么好的方式能发挥二分查找的优势呢?
答案是二分查找树,左侧数据小于节点,右侧数据大于节点
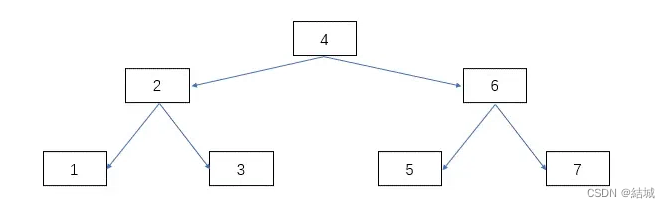
但是有个极端情况,一直加入的是大于(或者小于)当前节点值得节点,那么二分查找树会退化成链表,就没法二分查找了
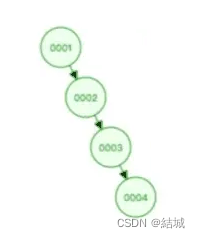
为解决这个问题,可以用平衡二叉查找树(AVL树),比二分查找树多了一个限制条件:每个节点得左右子树高度差不超过1。
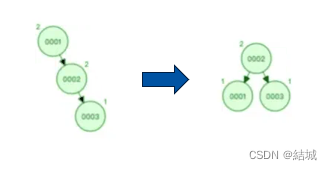
红黑树也是平衡二叉树,但约束条件比较复杂,涉及左旋、右旋等。
不管是AVL树还是红黑树都是二叉树,就存在着一个问题——节点数量多的时候,深度很深,还是会增加磁盘io次数。
进一步,人们提出B树,也就是平衡M叉树,一层多放几个,比只放两个节点会好一些,降低树的深度。M是B树的阶,要求一个节点最多有M-1个值和M个子节点,多的话就分裂。

B树的数据和索引都存到节点中,也就是说找到了数据所在节点就能获取到数据了。但实际上,你每次从磁盘读入都是索引+记录,很大概率记录占用空间更大,那我一次读进内存,假设不是我要的,那我还不如一次多读点索引进来供我选择。而且B树还有一个问题,我想做范围查询假设要查5-8的数,那我就得做搜索,还得回退,又是一堆io,麻烦。
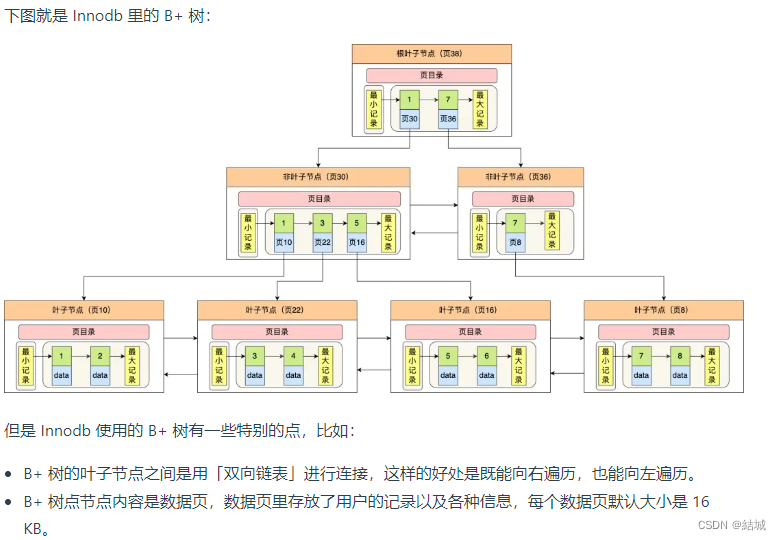
**重点:**因此B+树对B树做了升级,只有叶子节点存储了数据,其余节点只存索引,这样一次能读到更多索引。同时B+树的叶子节点之间也有链接,形成了链表,也就很好的支持了范围查询。

对比B树和B+树:
- 单个查询:B树可能会快,因为可能不用到叶子节点就查到了,但是其波动很大,可能是叶子节点可能是非叶子节点。而B+树非叶子节点存放索引数量更多,比B树矮胖,更少io次数搜索到叶子节点。
- 插入删除:B树可能会导致复杂的树结构变化;而B+树有很多冗余信息在非叶子节点上,基本不太会引起树的结构很大变化。
- 范围查询:B树肯定是要树的遍历才行;B+树则因为叶子节点之间的链接,很好的支持了范围查询。
Mysql的B+树做出了进一步改动,叶子节点是双向链表。对于聚簇索引,叶子节点的数据是具体的记录(实际数据);对于二级索引,叶子节点的数据是主键值。