哈希的应用
一、位图
情景:给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中???
看到查找元素的范围,暴力肯定是过不了的,我们要么二分要么哈希,但是二分要求排序,题目说没排过序,只剩下哈希,但是如果用正常的哈希表肯定不行,数据量太大了(可以算一下,大概15G),根本加载不进内存,更别谈放到哈希表中了,那怎么办?
这时候就需要用到位图---本质就是状态压缩版的哈希表,用一个比特位表示一个数字,大大压缩了数据量,(整形是4字节,如果是哈希表只能用来表示一个数字,但是位图可以用来表示4*8=32个数),数据量缩小了32倍,大概0.5G,具体的实现如下
namespace zxws
{template <size_t N=100>class bitset{public:bitset(){bit.resize(N/32+1);}void set(size_t x)//增{size_t i = x / 32;size_t j = x % 32;bit[i] |= (1u << j);//1u代表unsigned int类型的1}void reset(size_t x)//删{size_t i = x / 32;size_t j = x % 32;bit[i] &= ~(1u << j);}bool test(size_t x)//查{size_t i = x / 32;size_t j = x % 32;return (bit[i] >> j) & 1u;}private:vector<int>bit;};
}模拟实现没啥难度,就是要了解位运算,当然这只是位图的最重要的几个函数,还有一些其他的不常用的就不模拟实现了,有兴趣大家可以去查看文档
那么了解了位图的实现原理,我们再来看看下面的几个题
1. 给定100亿个整数,设计算法找到只出现一次的整数?2. 给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?3. 位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
namespace zxws
{template <size_t N = 100>class twobitset{public:void set(size_t x){size_t i = x / 32;size_t j = x % 32;if (bs1.test(x) == false && bs2.test(x) == false)//00->01{bs1.set(x);}else if (bs1.test(x) == true && bs2.test(x) == false)//01->10{bs1.reset(x);bs2.set(x);}}void test(size_t x){return bs1.test(x) == true && bs2.test(x) == false;//01--代表只出现一次}private:bitset<N>bs1;bitset<N>bs2;};
}题2:找文件交集,这个就很明显了,两个位图分别存放两个文件中的数字,然后比特位之间&一下,比特位上为1的就是交集
题3:这题其实和第1题一样,都是查看数字出现次数,要求不出现两次,即有没出现,出现1次,出现2次和出现2次以上四个状态,两个位图正好够了,实现同题1
二、布隆过滤器
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间
实现原理图

一般来说用三个哈希函数就差不多了

上图是网上的研究数据显示结果,仅供参考(k,m,n满足上诉关系时,不容易发生哈希冲突)
布隆过滤器的作用范围还是很广泛的,尤其是在不怎么关心某一个东西是否真的存在的场景下,举个例子,比如说取用户ID,当你取的id没人用时,OK你创建成功,当你取的id显示有人用时,如果是真的有人用了,那我们就换一个,如果没人用,它误判了,那我们也就是不能用这个id而已,没有啥太大影响,这时布隆过滤器就非常合适
当然如果说用户投诉说明明没人用这个id,却不让用,要求我们修复bug,这时我们只要让在布隆过滤器过滤后显示为存在的数据再去数据库中校验一下即可,
当然也有人会觉得反正都要去数据库校验还要布隆过滤器干嘛,注意:1.布隆过滤器它为啥叫过滤器,关键就是它只能确定不存在的数据,不能确定存在的数据。2.网络上通讯会比较耗时,如果每一个id的确认都需要与服务器上的数据库校验,就会浪费时间
实现如下
//哈希函数就自行去网上找哪些不容易产生哈希冲突的就行
template <size_t N, class K=string, class HashFunc1=HashFun<K>, class HashFunc2=DGBHash<K>, class HashFunc3=APHash<K> >
class BloomFiler {
public:void set(const K& key){size_t hash1 = HashFunc1()(key) % N;size_t hash2 = HashFunc2()(key) % N;size_t hash3 = HashFunc3()(key) % N;_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);}bool test(const K& key){size_t hash1 = HashFunc1()(key) % N;size_t hash2 = HashFunc2()(key) % N;size_t hash3 = HashFunc3()(key) % N;if (_bs.test(hash1) == false|| _bs.test(hash2) == false|| _bs.test(hash3) == false)return false;return true;}
private:bitset<N*5>_bs;
};两个问题:
1. 给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法(具体下面一个专题讲)
2. 如何扩展BloomFilter使得它支持删除元素的操作?一般来说是不能支持的,因为删除一个元素的映射会影响其他元素的哈希映射(因为它们会出现冲突),但是我们可以给它们加一个引用计数,这样就能在删除它的同时不影响其他元素的映射
优点1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关2. 哈希函数相互之间没有关系,方便硬件并行运算3. 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势4. 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势5. 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
三、哈希分割---哈希思想的扩展
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址?如何找到top K的IP?
100G的file很显然太大,我们的想法是将它分割成一个个小文件,然后在小文件中计数,我们将文件按Hash(id) % 100,得到100个1G的小文件(理想情况),然后我们就可以在小文件中统计每个id出现的次数(因为同一个id经过哈希映射会在同一个小文件中),但是,上面的只是理想情况,如果某一个小文件的大小为10G,也就是分完之后还是太大了,我们又该怎么办?
出现上诉情况共分两种可能:
1.相同的id太多
2.哈希冲突太多,导致多个不同的id都放在了同一个小文件中
如果是情况一,我们不用管,map中只会插入一次这个id,空间足够
如果是情况二,会报内存错误,这时我们就对这个小文件进行二次哈希分割即可
top K问题用堆实现就行,之前再二叉树数据结构中讲过的
下面,我们回过头去看看
给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法
近似算法就是用布隆过滤器,但是精确的算法呢?
这个query的大小也要考虑到,假设query的大小为50字节,那么一共5000亿字节,约等于500G,很明显了哈希切割,当然我们得先将query转成整数,Hash(query)%500,两个文件各自分成500个1G的小文件(理想情况),这样两个文件中相同的query会分别放在同一个余数的两个小文件中,如下图
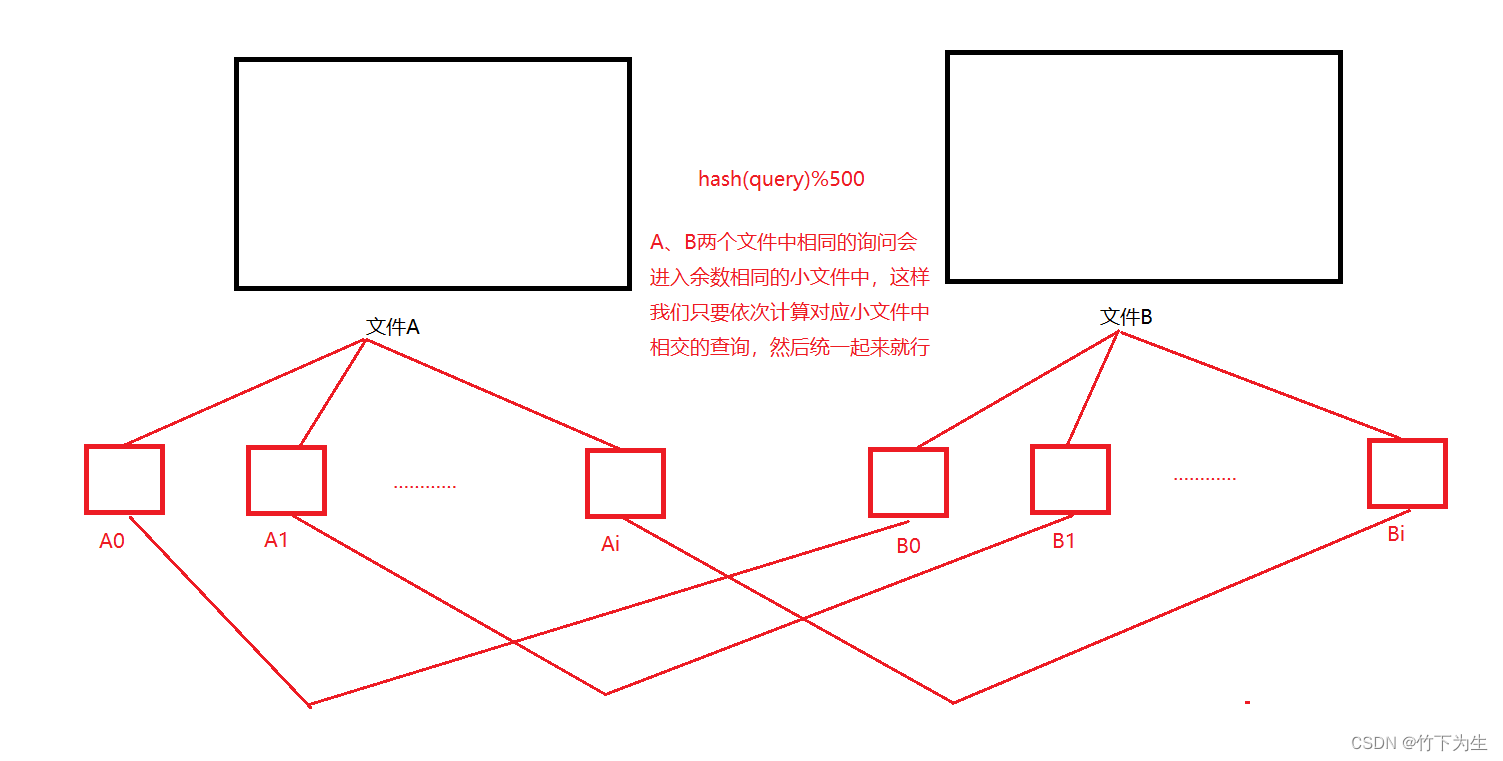
当然它也会出现小文件太大的情况,处理方法同上,注意这个不能用位图的原因是query里面存的不一定是整数,这样不同的query查询也有可能映射到用一个比特位(这也是布隆过滤器不准确的原因之一),就不精确了
如果上诉内容对你理解哈希有帮助的话,不要忘记点赞+评论哟!!!