文章目录
- 202. 快乐数
- 解法:
- 11. 盛最多水的容器
- 解法:
202. 快乐数


原题链接
拿到题,我们先看题干
把一个整数替换为每个位置上的数字平方和,有两种情况:
- 重复这个过程始终不到 1(无限死循环)
- 结果变成 1(快乐数)
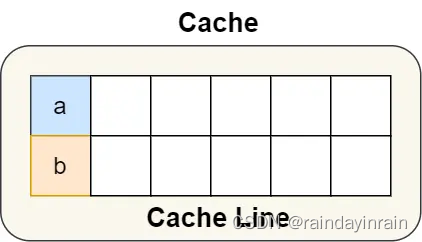
接下来我们画图看一下是不是这两种情况
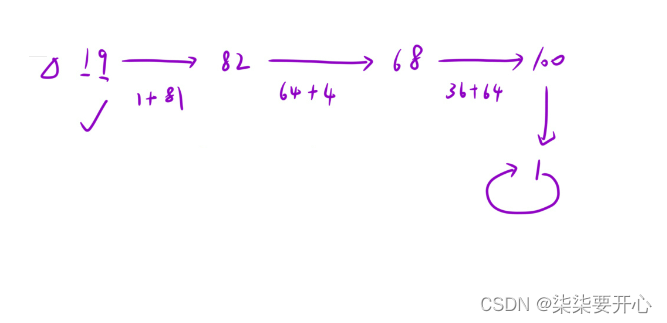
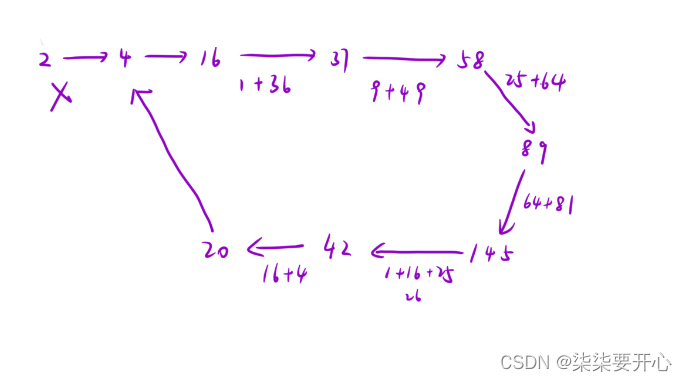
画完图我们就可以发现,这个跟曾经数据结构学过的判断链表是否有环非常相似
判断是不是快乐数,就是看入环的数字是几,如果是 1 那么就是快乐数
解法:
(快慢双指针)
- 定义快慢双指针 slow 和 fast
- 慢指针每次向后移动一位
快指针每次向后移动两位 - 判断相遇的值是不是 1
class Solution {public int isSum(int n) {int sum = 0;while(n != 0) {int t = n % 10;sum += t*t;n = n / 10;}return sum;}public boolean isHappy(int n) {int slow = n;int fast = isSum(n);while(slow != fast) {slow = isSum(slow);fast = isSum(isSum(fast));}return slow == 1;}
}
11. 盛最多水的容器


[原题链接](https://leetcode.cn/problems/container-with-most-water/
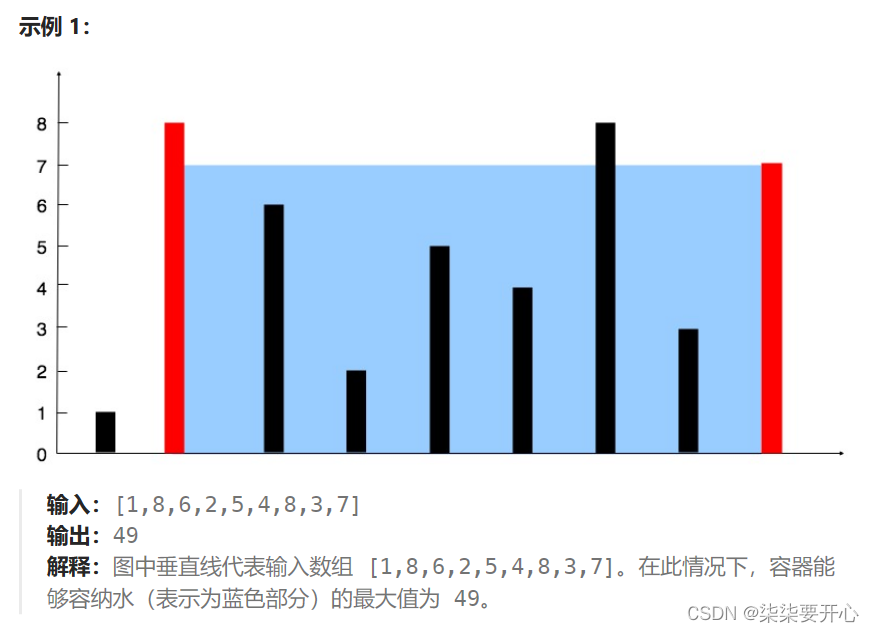
先看题干,貌似就是求体积,再看示例,就是求两段之间最小的那个值 乘 两段之间的差值
解法:
一:(暴力枚举)
运用两个 for 循环进行枚举
但是时间复杂度为 O(n2)
会导致时间溢出
二:(利用单调性,使用双指针)
这里我们先看一下什么是单调性

先用 [ 6, 2, 5, 4 ] 来举例
6 > 4
所以如果 4 不变,从右向左一个一个计算体积
4 * 3 = 12
2 * 2 = 4
4 * 1 = 4
发现只有第一个的体积是最大的
这样我们可以直接删去 4 ,从 6 开始向 5 进行遍历
这就是单调性
利用这样的规律,我们在看原数组,我们就可以这样解题
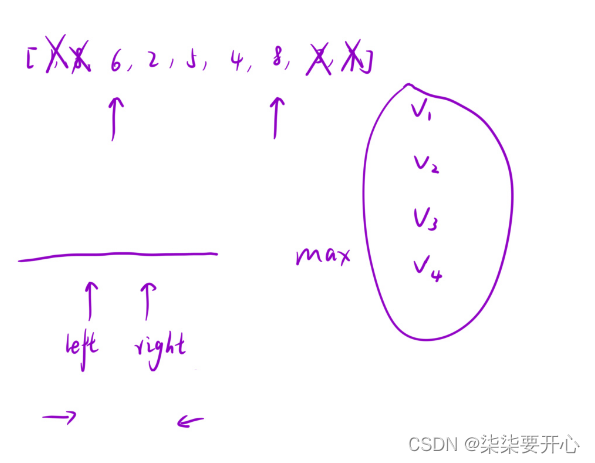
- 定义双指针 left 和 right
- 把 最大的体积存放到 ret 中
- left 和 right 比较大小
left < right : left ++;
left > right : right–; - 直到 left 和 right 相遇
class Solution {public int maxArea(int[] height) {int left = 0;int right = height.length-1;int ret = 0;while(left < right) {int v = Math.min(height[left],height[right]) * (right - left);ret = Math.max(ret,v);if(height[left] < height[right]) {left++;}else {right--;} }return ret;}
}