DBS note6：Hashing（哈希存储）

一、一般策略

二、算法简述

三、哈希缺点（Drawbacks of Hashing）

四、举例

五、外部哈希的分析

一、一般策略

由于我们无法一次性将所有数据放入内存中，我们需要构建多个不同的哈希表并将它们连接在一起。然而，这个想法存在一个问题。

如果我们构建了两个分开的哈希表，它们中都包含相同的值（例如，“Brian” 同时出现在两个表中），那么连接这两个表将导致一些 “Brian” 并非相邻。

为了解决这个问题，在将内存中的数据构建成哈希表之前，我们需要确保如果某个特定值存在于内存中，那么它的所有出现也都在内存中。换句话说，如果 “Brian” 至少在内存中出现一次，那么只有当我们的数据中的每个 “Brian” 出现都在内存中时，我们才能构建哈希表。这确保了值只能出现在一个哈希表中，使得哈希表可以安全连接。

二、算法简述

我们将使用分治算法来解决这个问题。在 “divide” 阶段，我们执行分区传递，在 “conquer” 阶段，我们构建哈希表。就像在排序笔记中一样，我们假设有 B 个可用的缓冲帧。在对数据进行哈希时，我们将使用其中 1 个缓冲区作为输入缓冲区，剩下的 B-1 个缓冲区作为输出缓冲区。

我们开始将数据从磁盘流式传输到一个输入缓冲区。有了这些输入数据后，我们希望将它们分成几个部分。每个部分都是一组页面，这些页面上的值通过特定的哈希函数都被映射到相同的哈希值。在第一轮分割中，我们会将输入缓冲区中的每条记录通过哈希函数分到 B-1 个部分中，每个部分对应 B-1 个输出缓冲区中的一个。如果某个输出缓冲区已满，相应的页面就会被写入磁盘，然后哈希过程继续。所有来自同一缓冲区的刷新页面都会在磁盘上相邻存储。第一轮分割结束时，我们在磁盘上存储了 B-1 个部分，每个部分的数据都是连续存储的。

分区的一个重要特性是，如果某个值出现在一个分区中，我们数据中所有该值的出现都会位于同一个分区。这是因为相同的值将被哈希到相同的位置。例如，如果 “Brian” 出现在一个分区中， “Brian” 将不会出现在任何其他分区中。

在第一轮分割后，我们得到了 B-1 个大小不同的分区。对于能够放入内存的分区（分区的大小小于或等于 B 页），我们可以直接进入“conquer ”阶段，开始构建哈希表。对于太大的分区，我们需要使用不同于第一轮中使用的哈希函数进行递归分区。为什么要使用不同的哈希函数呢？如果我们重复使用原始函数，每个值都将哈希到其原始分区，因此分区的大小不会减小。我们可以使用不同的哈希函数进行递归分区，直到所有分区最多有 B 页为止。

一旦所有的分区都能够放入内存，并且相同的值都出现在同一个分区中（根据分区的特性），我们就可以开始 “conquer” 阶段。首先，我们为构建最终哈希表选择一个新的哈希函数。然后，对于每个分区，我们将分区流式传输到内存中，使用新的哈希函数创建哈希表，并将生成的哈希表刷新回磁盘。

三、哈希缺点（Drawbacks of Hashing）

需要注意的是，哈希对数据倾斜非常敏感。数据倾斜发生在我们进行哈希的值不符合均匀分布的情况下。由于哈希分区的特性（相同值的所有哈希最终都会在同一个分区中），数据倾斜可能导致分区大小非常不均匀，这对我们的目的来说是不理想的。此外，并非所有的哈希函数都是相同的。在最理想的情况下，我们的哈希函数是一个均匀的哈希函数，将数据分成“均匀”的大小相等的分区。然而，哈希函数通常是非均匀的，会在所有分区之间不均匀地分布数据。在本课程中，除非另有说明，我们将使用均匀哈希函数。在下面的两个图像中，圆柱体表示在磁盘上发生的步骤，正方形表示在内存中发生的步骤，两者之间的线表示数据在磁盘和内存之间的流动。

下面的图像展示了哈希的两个阶段 - divide 和 conquer - 当不需要递归分区时。这意味着在初始分区后，所有分区都适合于 B 页内。请注意，在 “divide ” 阶段中，1 个缓冲页专用于输入缓冲区，其余的 B-1 个用于分区。然后，在 “conquer ” 阶段中，对每个单独的分区使用不同的哈希函数 $h_r$ 来形成内存中的哈希表。

下面的图像显示了递归分区。请注意，附加的阶段仅适用于大小大于 B 页的分区（灰色分区）。

四、举例

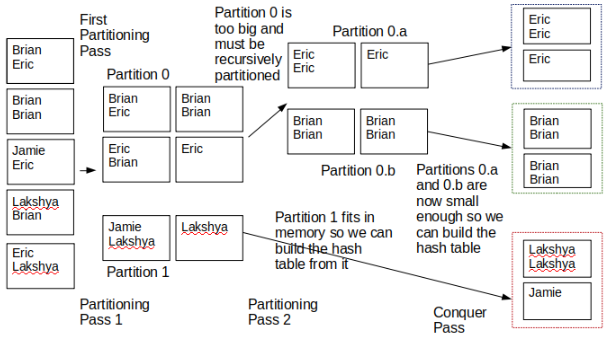
在以下示例中，我们假设我们有 B=3 个缓冲页可用。我们还假设对于第一个哈希函数，Brian 和 Eric 哈希到相同的值，但对于第二个哈希函数，它们哈希到不同的值，而 Jamie 和 Lakshya 对于第一个哈希函数哈希到相同的值。

在第一次分区传递（分区传递 1）后，分区 0 有 4 页，分区 1 有 2 页。分区 1 可以放入内存，但分区 0 不能。这意味着我们必须对分区 0 进行递归分区。

经过第二次分区传递后，分区 0 被分为两部分：分区 0.a 有 2 页，分区 0.b 有 2 页。由于分区 1 已经适应内存，所以在第二次分区传递期间它没有被分区。

一旦所有分区（0.a、0.b、1）适应内存，我们执行 "conquer" 并构建哈希表。可以看到在最终的 "conquer" 后，所有相同值都在一起，这是我们的最终目标。

五、外部哈希的分析

我们无法像排序算法中那样简单地创建一个计算I/O数量的公式，因为我们不知道分区的大小。我们首先需要认识到的一件事是，在分区后表的页数可能会增加。为了理解这一点，考虑下面的表，我们可以在一页上容纳两个整数：

[1, 2] [1, 4] [3, 4]

假设B=3，因此我们只将数据分为2个分区。假设1和3散列到分区1，2和4散列到分区2。分区后，分区1将包含：

[1, 1]，[3]

而分区2将包含：

[4, 2]，[4]

请注意，我们现在有4页，而我们一开始只有3页。因此，计算 I/O 数量的唯一可靠方法是查看每个阶段，看看将读取什么和将写入什么。设 m 为所需的总分区次数， $r_i$ 为第 i 个分区阶段需要读取的页数， $w_i$ 为第 i 个分区阶段需要写出的页数，X 为分区后我们需要构建哈希表的总页数。以下是 I/O 数量的公式：