CT3D
- 一、RPN for 3D Proposal Generation
- 二、Proposal-to-point Encoding Module
- 2.1、Proposal-to-point Embedding
- 2.2、Self-attention Encoding
- 三、Channel-wise Decoding Module
- 3.1、Standard Decoding
- 3.2、Channel-wise Re-weighting
- 3.3、Channel-wise Decoding Module
- 四、Detect head and Training Targets
- 五、训练losses
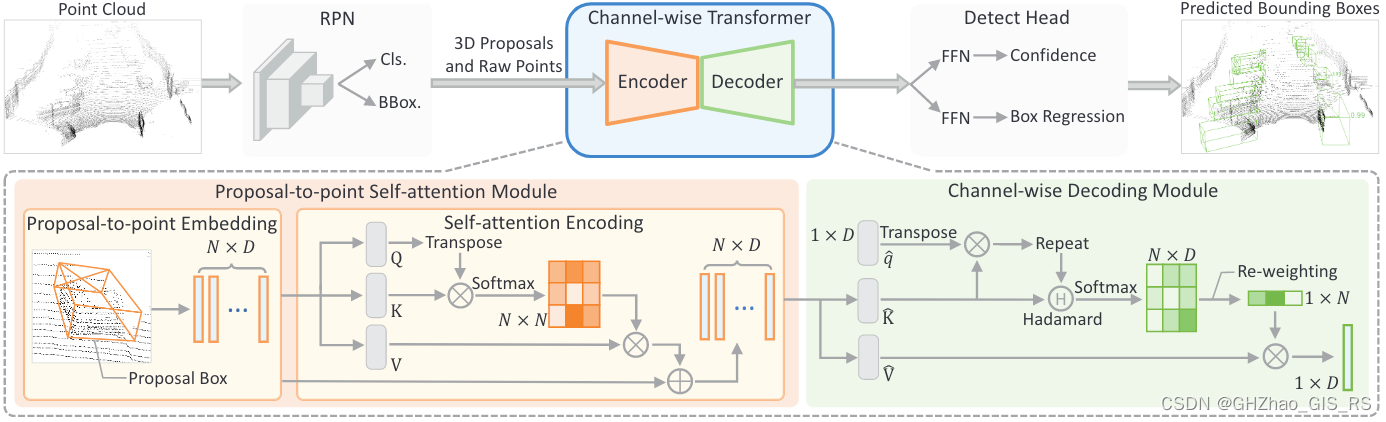
一、RPN for 3D Proposal Generation
就是基于单阶段的网络获取box作为Proposal,文章中使用的是Second网络,其他的如pointpillar、centerpoint都可以作为
CT3D的RPN网络。
二、Proposal-to-point Encoding Module
通过以下两个模块精修RPN输出的proposal:
1、将proposal特征映射到点的特征上(下图左)。
2、通过自注意力编码对proposal内点之间的相对关系进行建模来细化点的特征(下图右)。
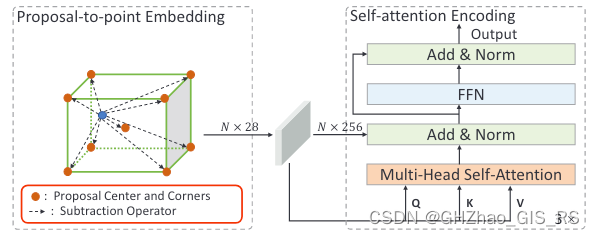
2.1、Proposal-to-point Embedding
对于给定的一个proposal,选择ROI区域内的点,ROI区域是一个没有高度限制的圆柱体,然后随机选取ROI范围内的256个点。
- 首先计算采样点和Proposal中心点的相对坐标, Δ p i c = p i − p c , ∀ p i ∈ N \Delta \boldsymbol{p}_{i}^{c}=\boldsymbol{p}_{i}-\boldsymbol{p}^{c}, \forall \boldsymbol{p}_{i} \in \mathcal{N} Δpic=pi−pc,∀pi∈N。
- 然后一个直接的做法是将Proposal的长、宽、高、和旋转角度信息直接拼接到每个点的特征上,即 [ Δ p i c , l c , w c , h c , θ c , f i r ] \left[\Delta \boldsymbol{p}_{i}^{c}, l^{c}, w^{c}, h^{c}, \theta^{c}, f_{i}^{r}\right] [Δpic,lc,wc,hc,θc,fir]。由于Transformer 编码器根据这种几何信息重新定向的效果可能较差,所以这种直接基于尺寸和方向的特征表示对于Proposal的优化帮助可能是有限的。
- 通过计算采样点和Proposal八个顶点的相对位置, Δ p i j = p i − p j , j = 1 , … , 8 \Delta \boldsymbol{p}_{i}^{j}=\boldsymbol{p}_{i}-\boldsymbol{p}^{j}, j=1, \ldots, 8 Δpij=pi−pj,j=1,…,8, p j {p}^{j} pj是第 j j j个顶点的坐标,这样长、宽、高和角度信息就被重新编码为不同纬度的距离信息。
- 最后将上述信息合并,并经多一个MLP网络上提升特征纬度。
f i = A ( [ Δ p i c , Δ p i 1 , … , Δ p i 8 , f i r ] ) ∈ R D \boldsymbol{f}_{i}=\mathcal{A}\left(\left[\Delta \boldsymbol{p}_{i}^{c}, \Delta \boldsymbol{p}_{i}^{1}, \ldots, \Delta \boldsymbol{p}_{i}^{8}, f_{i}^{r}\right]\right) \in \mathbb{R}^{D} fi=A([Δpic,Δpi1,…,Δpi8,fir])∈RD
2.2、Self-attention Encoding
随后将重新编码后的采样点送入多头自注意力层,然后接一个带有残差结构的FFN网络。除了没有位置编码外(在第一步中已经包含了位置信息),这种自注意力编码机制和NLP中的Transofrmer结构几乎一模一样。encoding具体细节略过。
三、Channel-wise Decoding Module
解码器模块是将编码器模块输出的所有点的特征聚合成一个全局特征,表示这个proposal的特征,用来做refine。标准的transformer的解码器的query embedding个数是M,Voxelnext解码器的query embedding的个数是1,主要原因是
- M个query embedding计算会特别慢,尤其是在Proposals的数量特别多的时候。
- M个query embedding通常对应M个输出,而目标检测的refine阶段,一个Proposal只对应一个输出。
3.1、Standard Decoding
标准解码策略是用一个D维可学习点向量作为query embedding,用所有点的所有通道来聚合点的特征,得到注意力全中 W W W,每个注意力head的解码权重计算公式如下:
w h ( S ) = σ ( q ^ h K ^ h T D ′ ) , h = 1 , … , H \boldsymbol{w}_{h}^{(S)}=\sigma\left(\frac{\hat{\boldsymbol{q}}_{h} \hat{\mathbf{K}}_{h}^{T}}{\sqrt{D^{\prime}}}\right), h=1, \ldots, H wh(S)=σ(D′q^hK^hT),h=1,…,H
其中 K h ^ \hat{K_h} Kh^是第h个head的key embedding,是通过编码器的输出投影得到的(其实就是1x1卷积,只是为了改变特征通道数,也可以不改变),size是[N,D]。 q h ^ \hat{q_h} qh^是相应的query embdding,这里就是1个随机生成的D维向量,size是[1,D],然后使用softmax进行归一化,得到解码权重向量,size是[1,N]。文章中给出了这个公式对应图示:
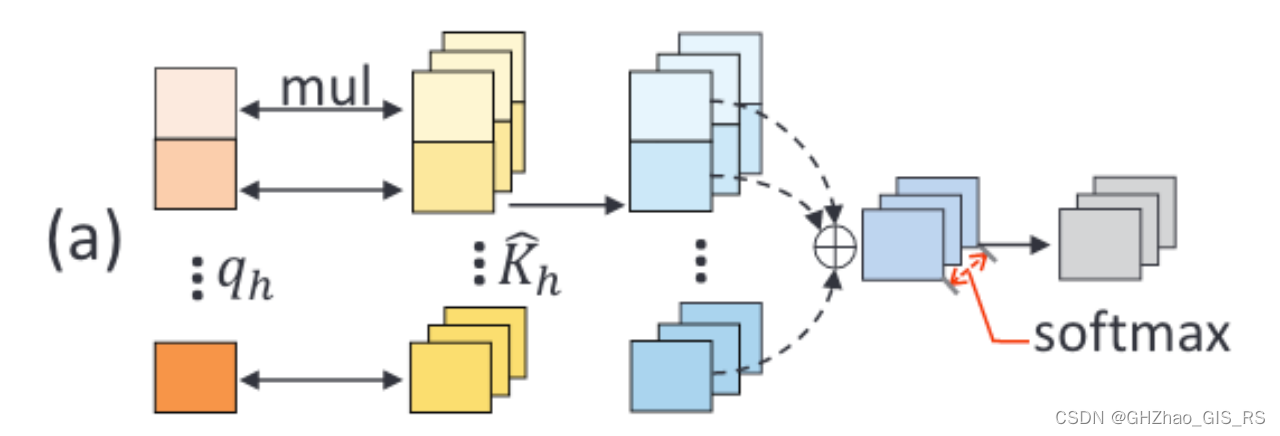
文章中说的到的解码权重向量是从简单的全局聚合导出的,缺乏全部通道建模,并且给了图展示,其实对照的图和公式不能一下看出来怎么是全局聚合,缺乏通道建模,下面我按照自己的理解方式尝试解释一下:
先看一个自注意力机制的计算过程:
假设原始向量是 X X X的维度是[3,4],即有3个token,每个token的特征通道是4,也可以理解为 X X X是3个点云的集合,每个点云的特征数为4,那一次自注意力机制的计算过程就是:
标准解码的权重向量是从简单的全局聚合计算得到的,缺乏局部通道建模,这对于学习点云的3D表面结构至关重要,因为不同通道通常在点云中表现出很强的几何关系。
3.2、Channel-wise Re-weighting
w h ( C ) = s ⋅ σ ^ ( K ^ h T D ′ ) , h = 1 , … , H \boldsymbol{w}_{h}^{(C)}=\boldsymbol{s} \cdot \hat{\sigma}\left(\frac{\hat{\mathbf{K}}_{h}^{T}}{\sqrt{D^{\prime}}}\right), h=1, \ldots, H wh(C)=s⋅σ^(D′K^hT),h=1,…,H
3.3、Channel-wise Decoding Module
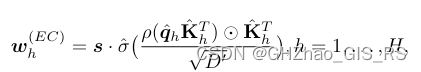
四、Detect head and Training Targets
将经过编码-解码模块的输出送入两个FFN网络中,预测得到confidence和相对于输入的Proposal的box残差值。
训练过程中confidence的真值被设置为Proposals和对应的gt的3D IoU值。confidence真值计算公式如下:
c t = min ( 1 , max ( 0 , I o U − α B α F − α B ) ) c^{t}=\min \left(1, \max \left(0, \frac{\mathrm{IoU}-\alpha_{B}}{\alpha_{F}-\alpha_{B}}\right)\right) ct=min(1,max(0,αF−αBIoU−αB))
box回归值的真值计算如下:
x t = x g − x c d , y t = y g − y c d , z t = z g − z c h c , l t = log ( l g l c ) , w t = log ( w g w c ) , h t = log ( h g h c ) , θ t = θ g − θ c , \begin{aligned} x^{t} & =\frac{x^{g}-x^{c}}{d}, y^{t}=\frac{y^{g}-y^{c}}{d}, z^{t}=\frac{z^{g}-z^{c}}{h^{c}}, \\ l^{t} & =\log \left(\frac{l^{g}}{l^{c}}\right), w^{t}=\log \left(\frac{w^{g}}{w^{c}}\right), h^{t}=\log \left(\frac{h^{g}}{h^{c}}\right), \\ \theta^{t} & =\theta^{g}-\theta^{c}, \end{aligned} xtltθt=dxg−xc,yt=dyg−yc,zt=hczg−zc,=log(lclg),wt=log(wcwg),ht=log(hchg),=θg−θc,
五、训练losses
CT3D是端到端的训练策略,包括三个损失,分别是RPN损失、confidence损失、box回归损失。

confidence损失用的是二元交叉墒计算。
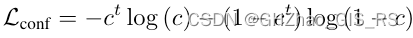
回归损失使用的是Smooth-L1计算,只有 I o U ≥ α R IoU ≥ α_R IoU≥αR 的Proposal才会用来计算回归损失。
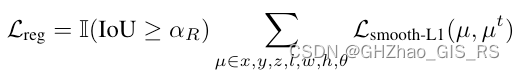







![[vue3] 使用 vite 创建vue3项目的详细流程](https://img-blog.csdnimg.cn/direct/4c7294755eb74506b4d4bc37c30270d2.png)