排序

将一组杂乱无章的数据按照一定规律排列起来。将无序序列排成一个有序序列。

排序方法的分类

储存介质：

• 内部排序：数据量不大，数据在内存，无需内外存交换数据。
• 外部排序：数据量较大，数据在外存（文件排序）。

比较器个数：

• 串行排序：单处理机（同一时刻比较一对元素）。
• 并行排序：多处理机（同一时刻比较多对元素）。

主要操作：

• 比较排序：用比较的方法。
  插入排序，交换排序，选择排序，归并排序
• 基数排序：不比较元素的大小，仅仅根据元素本身的取值确定其有序位置。

辅助空间：

• 原地排序：辅助空间用量为O（1）的排序方法。
• 非原地排序：辅助空间用量超过O（1）的排序方法。

稳定

• 稳定排序
• 非稳定排序

插入排序

直接插入排序

前提是数组中的元素是有序的。

#include<stdio.h>void PrintArr(int arr[],int l);
void InsertSort(int arr[], int l);//#define MAXSIZE 20	//设记录的值不超过20个
//#define  KeyType int//设关键字为整型量
//#define InfoType int //定义InfoType的其他数据项
//
//
//typedef struct {
//	KeyType key;//定义每个记录(数据元素)的结构
//	InfoType otherinfo;//其他数据项
//}RedType;
//
//typedef struct SqList {
//	RedType r[MAXSIZE + 1];//存储顺序表的结构
//						//r[0]一般做哨兵或者缓冲区
//	int length;//顺序表的长度
//}SqList;
//
//void InsertSort(SqList S) {
//	int i, j;
//	for (i = 2; i < S.length; i++) {
//		if (arr[i]  < arr[i - 1] ) {
//			arr[i]  = arr[0] ;
//		
//		for (j = i - 1; arr[j]  > arr[0] ; j--) {
//			arr[j + 1] = arr[j];//j的值都要依次向后移，进行插入
//		}
//		arr[j+1]  = arr[0] ;//这里直接将哨兵的值赋值给当前查出来正确的位置
//		}
//	}
//}void InsertSort(int arr[], int l) {int i = 0, j;int temp;printf("请输入要插入的数：");scanf_s("%d", &temp);arr[i] = temp;for (i = 2; i < l; i++) {if (arr[i] < arr[i - 1]) {arr[i]  = arr[0] ;for (j = i - 1; arr[j]  > arr[0] ; j--) {arr[j + 1] = arr[j];//j的值都要依次向后移，进行插入}arr[j+1]  = arr[0] ;//这里直接将哨兵的值赋值给当前查出来正确的位置}}PrintArr(arr, l);
}void PrintArr(int arr[],int l) {int i;for (i = 1; i <= l; i++) {printf("%d ", arr[i]);}
}int main() {int arr[10] = { 1,2,3,4,5,6,7,14, 12};InsertSort(arr,10);return 0;
}

折半插入排序

查找插入位置时采用折半查找法。

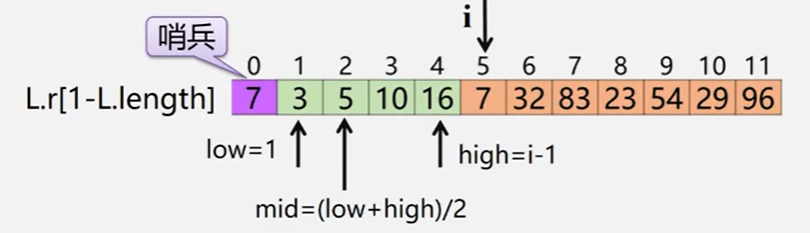
void BInsert(SqList &S) {int i, j,low,high,mid;for (int i = 2; i <= S.length; i++) {if (S.r[i].key < S.r[i - 1].key) {S.r[i] = S.r[0];low = 1, high = i - 1;while (low <= high) {mid = (low + high) / 2;if (S.r[0].key <S.r[mid].key) {high = mid - 1;}else {high = mid + 1;}}for (j = i - 1; j < high + 1; j--) {S.r[j - 1] = S.r[j];S.r[high + 1] = S.r[0];}}}
}

折半插入排序—算法分析

• 折半查找比顺序查找要快，所以折半插入排序就平均性能来说比直接插入排序要快；
• 他所需要的关键码比较次数与待排序对象序列排列无关，仅依赖于对象个数，在插入第i个对象时，需要经过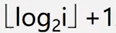次关键码比较，才能确定它应该插入的位置。
• 折半查找减少了比较次数，但没有减少移动次数。
• 平均性能优于直接插入排序。
• 时间复杂度为O(n的平方）。
• 空间复杂度为O（1）。
• 是一种稳定的排序方法。

希尔插入排序

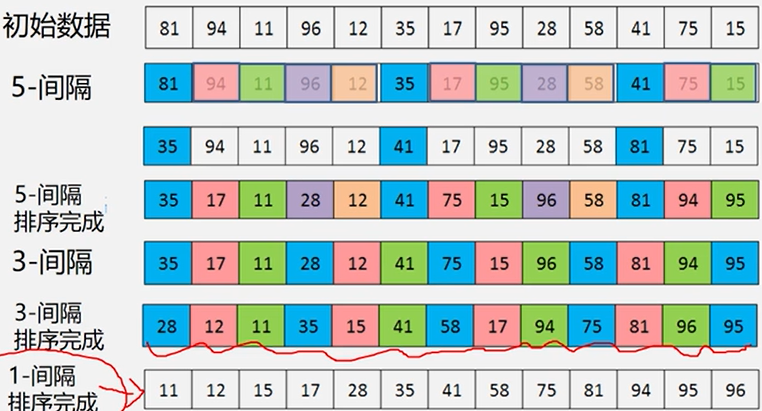
希尔排序的特点：

1. 一次移动，移动位置较大，跳跃式地接近排序后的最终位置。
2. 最后一次只需少量移动
3. 增量序列必须是递减的，最后一个必须是1.
4. 增量序列应该是互质的。

//希尔排序
void ShellInsert(SqList& L, int dk) {//对顺序表L进行一趟增量为dk的Shell排序，dk为增长因子int i,j;for (i = dk + 1; i <= L.length; ++i) {if (L.r[i].key < L.r[i - dk].key) {L.r[0] = L.r[i];for (j = i - dk; j > 0 && (L.r[0].key < L.r[j].key); j = j - dk) {L.r[j - dk] = L.r[j];}L.r[j + dk] = L.r[0];			}}
}void ShellSort(SqList& L, int dlta[], int t) {//按增量序列dlta[0..t-1]对顺序表L进行希尔排序for (int k = 0; k < t; k++) {ShellInsert(L, dlta[k]);//一趟增量为dlta[k]的插入排序}
}

希尔排序算法分析