Lattice-Based Blind Signatures: Short, Efficient, and Round-Optimal
CCS 2023

摘要

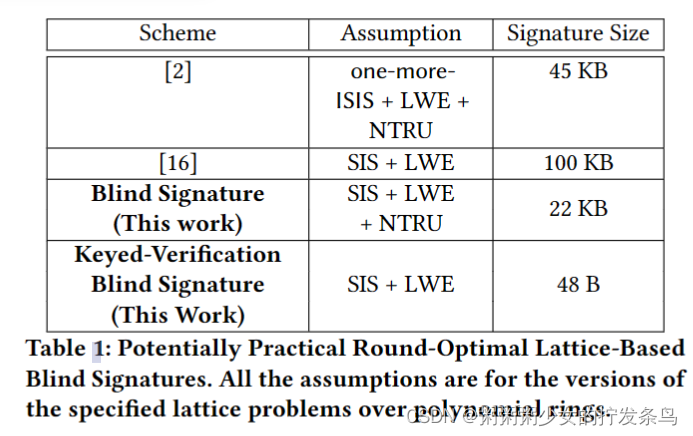
我们提出了一种基于随机预言机启发式和标准格问题（环/模块SIS/LWE和NTRU）的2轮盲签名协议，签名大小为22KB。该协议是全面优化的，并且具有小到60KB的转录本大小。该盲签名比基于del Pino和Katsumata的标准假设的最紧凑的基于格的方案（Crypto 2022）短约4倍，比Agrawal等人的方案短约2倍。（CCS 2022）基于他们新提出的又一个ISIS假设。我们还提出了一种“密钥验证”盲签名方案，其中验证器和签名者需要共享一个密钥。该方案的签名大小较小，仅为48字节，但还需要进一步的工作来探索其签名生成协议的效率。

引言

盲签名是一种协议，在该协议中，用户从签名者那里获得消息的签名，而签名者不需要了解消息的任何信息，是基于隐私的密码学的基本原理之一[13]。由于数字货币的出现和人们日益增长的隐私期望，它们的重要性正在稳步增加。根据各种假设，已经有许多实际的实例对这个原语进行了实例化，目前有在国家层面部署这些原语以创建中央银行数字货币的具体建议（例如[14]）。

最近的另一个重要发展是，基于因子分解和离散对数等假设的密码学正在向基于推测量子安全假设的密码学过渡。经过6年的NIST量子后标准化工作，最近产生了四种公钥方案（一种加密和三种数字签名），将在明年进行标准化[31]，美国国家安全局现在要求必须在2030年代初全面过渡到量子安全密码学[32]。这一时间线很可能与盲签名和其他即将推出的基于隐私的加密方案的大规模部署密切吻合；这强烈地意味着这些也需要是量子安全的。但是，尽管有许多基于经典假设的非常有效的盲签名，但缺乏对量子安全盲签名的研究。【[14]标题中的“量子安全”仅指特定的安全属性——然而，整个方案并不量子安全，因为它基于RSA。】

最近，两项基于格的盲签名提案改善了这一现状，尽管其效率不如经典签名，但肯定处于实用领域。[16]的方案是基于标准格假设【我们讨论的所有格假设和本文中的格假设都是多项式结构的上格。】的盲签名，签名大小约为100KB，总通信量低于1兆字节。[2]中的方案基于该文提出的新的一个多ISIS假设，其优点是该方案更高效，大小约为45KB，并且创建签名所需的通信更少。

在我们的工作中，我们改进了现有技术，提出了一种基于标准格假设的实用盲签名，将签名大小缩小到大约22KB。我们还提出了一种密钥验证盲签名方案，其中签名只有48字节，但后者的缺点是签名的生成效率较低，并且验证需要签名者的密钥。

我们的方案是轮最优的，这意味着签名是在两轮之后生成的。圆优化在实践中是有用的，因为通信延迟通常是交互式协议中的主要瓶颈。它还可以非常有用，因为它允许其中一方离线预计算协议的整个部分，这甚至可以允许相当低功率的用户参与协议。此外，2轮盲签名不必担心涉及签名协议的并发执行的微妙问题，这可能会使多轮盲签名的设计复杂化，并在过去导致具体的攻击[7]。

我们的协议使用两种不同类型的零知识证明。签名验证中使用的零知识证明是[26]证明格关系知识的一种有效的基于格的证明。然而，在用户和签名者之间的第一轮交互中，我们需要证明加密哈希函数的输入知识。由于此类函数的结构不如格关系，因此这一部分的计算成本更高，尽管并不令人望而却步（请参阅第1.1节中的讨论）。由于签名过程中最昂贵的部分发生在第一个流期间，因此我们的协议特别适合于提前知道要签名的消息的应用，从而可以离线地预先计算这些证明。一个这样的应用程序是电子现金（在[13]中激发盲签名的应用程序），其中用户要求随机消息的签名，可以在与签名者（即银行）的交互开始之前选择。

下面我们给出了我们的结构的详细草图。我们假设读者对基本的格密码术有些熟悉。