调试复习
调试可谓是 “贯穿” 了程序员的一生,调试的重要性,就不再赘述啦!如果你还不知道什么是调试,可以看看 Windows 系统的 Visual Studio 是如何调试的:➡️ visual stuudio 使用调试技巧
下载调试软件 gdb
yum install gdb -y
gdb 的使用
gdb 的使用非常简单:
gdb 可执行文件
这是一段简单的代码:
#include<stdio.h>int main()
{printf("hello gdb\n");return 0;
}
这是 makefile 文件:
test:test.cgcc -o $@ $^ -std=c99
.PHONY:clean
clean:rm -f test
make 生成可执行文件之后,我们来看看是否能够启动 gdb 调试:
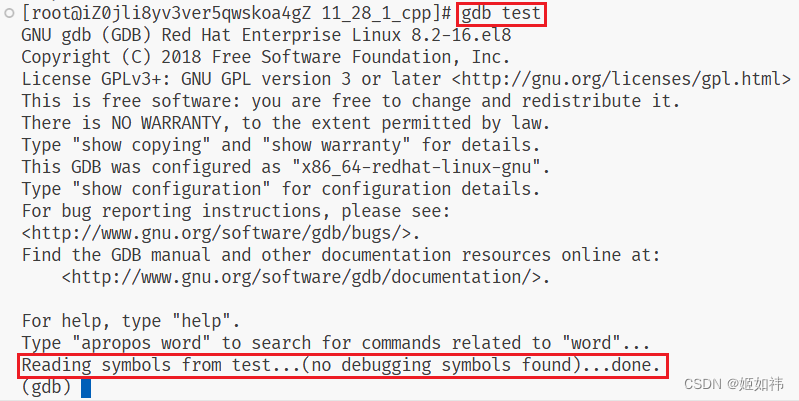
我们看到出现了报错:可执行文件中没有调试信息。这是因为 linux 环境下 gcc 形成的可执行程序默认是以 release 的形式发布的,release 版本的可执行程序当然不包含调试信息啦!
于是,我们需要以 debug 的方式发布可执行程序,只需要加一个 -g 的选项就可以啦!
# 这是 makefile 文件
test:test.cgcc -o $@ $^ -g -std=c99
.PHONY:clean
clean:rm -f test
那么如何看到可执行程序中是否有调试信息呢?我们都知道 linux 环境下的可执行程序是一种 elf 格式的文件,我们只要打开这个 elf 格式的文件,就能看到啦!
readelf -S 可执行程序
我们可以看到 debug 方式发布的可执行程序确实多了调式信息。(文件比较长,下图中只截取了一部分)

调试前的准备
我们来写一个简单的程序,作为调试之前的准备工作吧!
test.c
#include<stdio.h>
#include "function.h"int multiple(int x, int y)
{int ret = x * y;return ret;
}
int main()
{int a = 2, b = 3;int sum = 0;sum = Add(a, b);printf("a + b: %d\n", sum);int times = multiple(a, b);for(int i = 0; i < times; i++){printf("hello gdb %d\n", i);}return 0;
}
function.h
#pragma onceint Add(int x, int y);
function.c
#include "function.h"int Add(int x, int y)
{return x + y;
}
调试命令一览
gdb 可执行程序 #开始调试
quit/q #退出调试
l 数字 #显示代码,默认是 10 行
r #运行程序
b 行号 #在main函数所在文件的指定行打断点
b 文件名:行号 #在指定文件的指定行号打断点
b 函数名 #在指定函数的第一行代码处打断点
info b #查看所有断点信息
d 断点编号 #删除断点# r 开始调试之后n #逐过程运行
s #逐语句执行
p 变量 #查看变量的值
display 变量 #变量值常显示,类似于 visual studio 的监视窗口
undisplay 变量 #取消变量的长显示
untill 行号 #在函数内跳转到指定行
finish #执行完当前行所在的函数
c #运行到下一个断点处
disable 断点编号 #禁用指定断点
enable 断点编号 #恢复禁用的断点
set var 变量=值 #类比 visual studio 中的条件断点
bt #查看调用堆栈
info locals #查看本地变量(局部变量)
下面我会选择几个比较不好理解的讲讲
l 数字
l 默认显示 10 行,gdb 会记住上一条命令,回车就可以继续执行上一条命令。
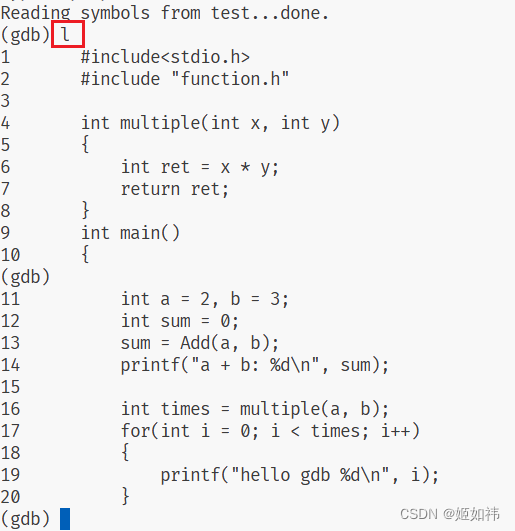
b 文件名:行号
这个命令在多文件的调试中可能会用到:

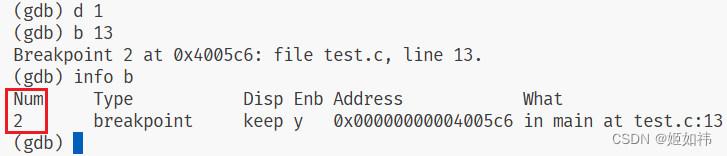
d 断点编号
断点编号是什么呢?查看断点编号需要使用 info b 命令:

其中这个 Num 就是断点编号啦!

可以看到删除断点之后就查看不到断点的信息啦!
删除刚刚的断点之后我们再打一个断点,发现断点编号并不是 1,说明断点编号是递增的!
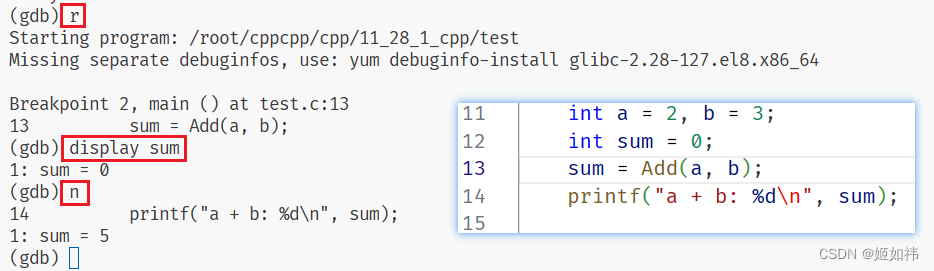
display 变量
可以动态显示一个变量的内容,类似于监视窗口。
我们使用 r 运行程序,开始调试。display num 看到:sum = 0 没问题,然后 n 逐过程运行。发现 sum 变成了 5。这就相当于监视窗口不是嘛!
finish
执行完当前行所在的函数,这是什么意思呢?我们在第六 6 行打一个断点,看看效果就知道了!
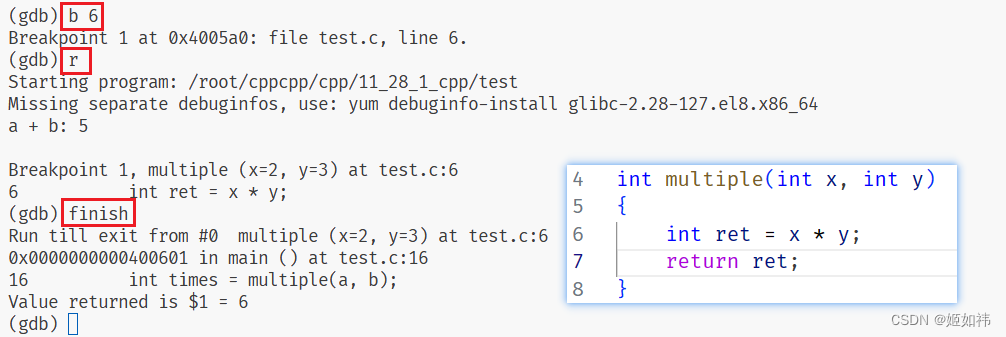
效果就是直接完成了当前行所在函数的运行
disable 断点编号
这个命令可以禁用断点,visual studio 也是可以的!
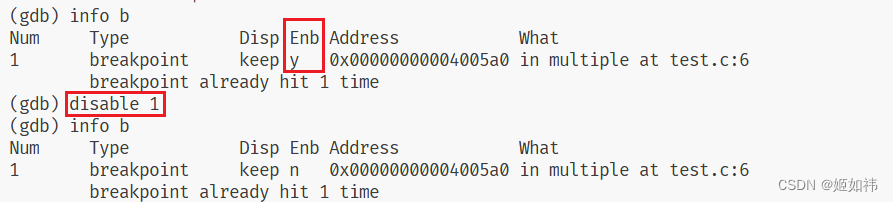
禁用 1 号断点之后,我们查看断点信息,发现 Enb 属性变成了 n。这就表示这个断点被禁用了!
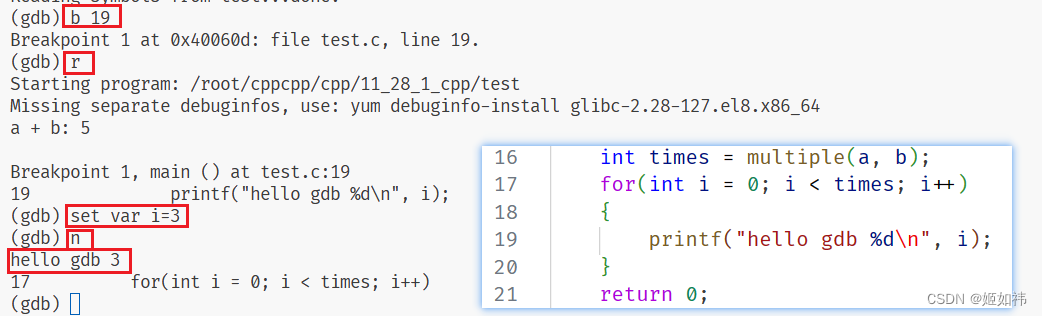
set var 变量=值
我们在 19 行打一个断点,然后运行程序,开始调试,再然后 set var i=3 运行之后,我们发现打印的就是 hello gdb 3 这是不是和 visual studio 中的条件断点一个味儿!