2017年五一杯数学建模

A题 公交车排班问题

原题再现

  随着徐州市经济的快速发展，公交车系统对于人们的出行扮演着越来越重要的角色。在公交车资源有限的情况下，合理的编排公交车的行车计划成为公交公司亟待解决的问题。以下给出公交车排班问题中的部分名词说明和假设。
  (1) 班次：1 辆公交车从起点出发到达终点停止为 1 个班次。
  (2) 公交车公司有两种类型的班车：单班车和双班车。除非特殊说明，单班车和双班车都可以用于公交车排班。
  (3) 单班车：由同一个驾驶员驾驶的公交车。单班车通常要求在早高峰跑 2-3 个班次，晚高峰2-3 个班次，一天不超过 5 个班次。
  (4) 双班车：由两个驾驶员驾驶的公交车。双班车要求上、下午各一个司机，上午和下午司机的工作时间尽可能均匀，并且都不超过 8 小时。每辆双班车一天运行不超过 10 个班次。
  (5) 公交车运行的单程时间，已经包含乘客在各站(包括起点和终点)的上下车时间。
  (6) 假设每辆公交车可以运行 1 整天不需要加油。
  (7) 末班车的发车时间，可以在原有发车间隔的基础上调整 2 分钟（±2 分钟）。
  (8) 本题以简单的环路公交路线为例，即公交车从 A 点出发，经过一系列站点后再次回到 A点为 1 个班次。
  (9) 最短停站时间是指公交车完成 1 个班次之后，开始运行下一个班次之前，需要在终点停留的最短的时间。在问题 1-3 中，每辆公交车的最短停站时间为 0，即：公交车回到终点后不需要停留，可以继续进行下一班次的运行。
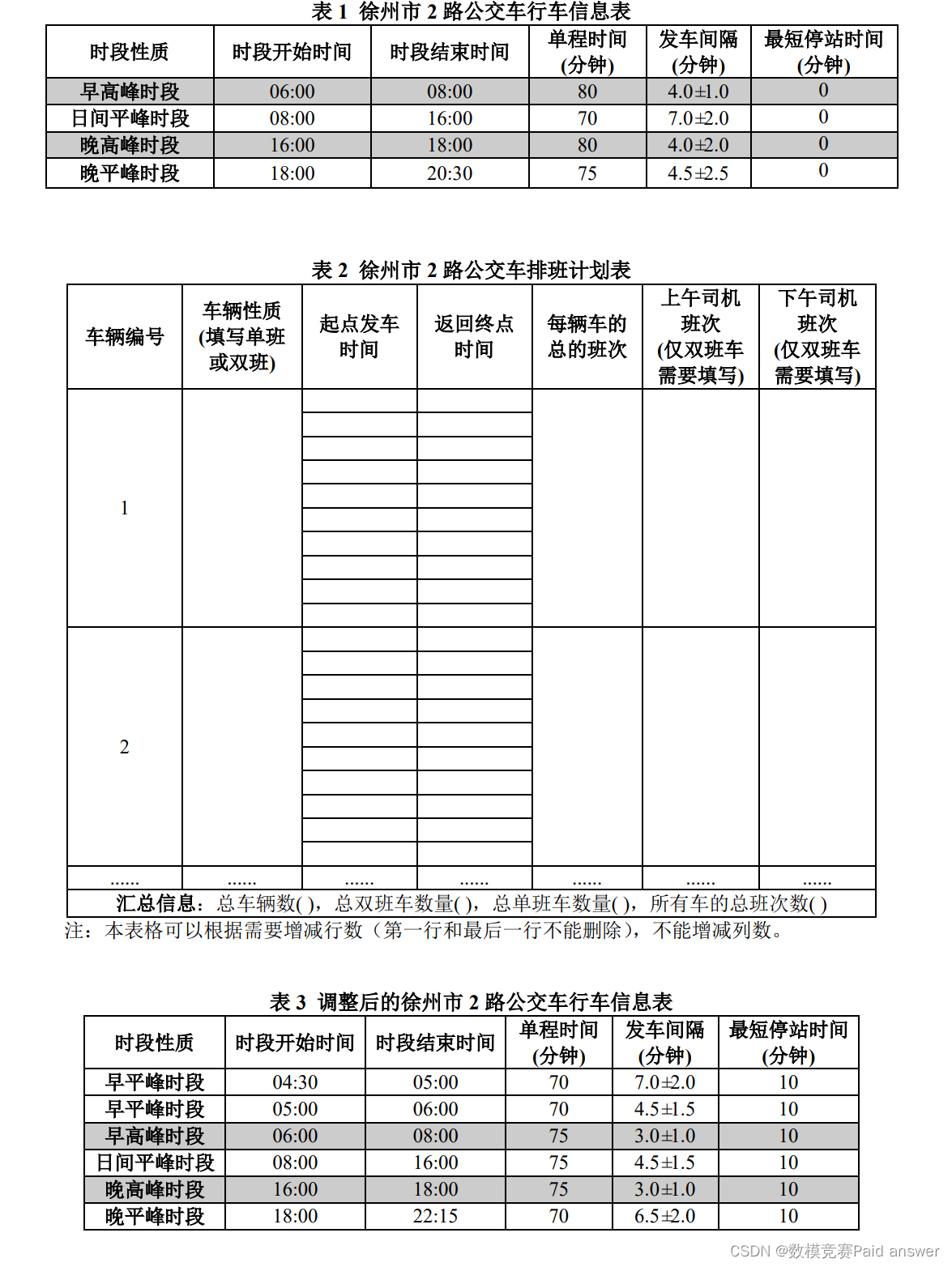
  问题 1. 徐州市 2 路公交车，从徐州火车站出发后经沿途站点后回到徐州火车站，2 路公交车行车信息如表 1。请建立数学模型，计算徐州市 2 路公交车，在早高峰时段(6:00-8:00)运行所需要使用的最少公交车数辆(需要给出含单班车和双班车各多少辆)。
  问题 2. 在问题 1 的基础上，请建立数学模型并设计相应的求解算法，给出徐州市 2 路公交车完成一整天的运行所需要最少的公交车的数辆(需要给出含单班车和双班车各多少辆)，并按照表 2 的格式给出公交车排班计划表。
  问题 3. 在问题 2 的基础上，如果要求单班车不少于 3 辆，请建立数学模型并设计相应的求解算法，给出徐州市 2 路公交车完成一整天的运行所需要最少的公交车的数辆(需要给出含单班车和双班车各多少辆)，并按照表 2 的格式给出公交车排班计划表。
  问题 4. 在公交车排班过程中，除以上要求之外，还需要考虑如下的实际因素的限制：
  (a) 单班车司机不安排吃饭，所有双班车司机都安排吃饭(早餐和晚餐)，每餐饭需要 20 分钟用餐时间。早餐 8:00 开始供应，10:00 截止；晚餐 18:00 开始供应，20:00 截止。
  (b) 限定双班车辆的数辆为 19 辆。
  © 双班车辆运行 5 班次以后，上午、下午班司机进行换班，换班时间最少为 20 分钟(含最短停站时间)。
  请建立数学模型并设计相应的求解算法，并以表 3 给出的行车信息表为例，给出徐州市 2 路公交车行车信息调整后，完成一整天的运行所需要最少的公交车的数辆(需要给出含单班车和双班车各多少辆)，并按照表 2 的格式给出公交车排班计划表。

整体求解过程概述(摘要)

  本文主要研究公交公司根据全天出行高峰的分布，各时间段单程时间和发车间隔时间不同的特点，制定出使得公交车在各时间段运行所需要使用的最少公交车数量的排班计划方案，本文构造单双班车综合发车计划矩阵并采用行列迭代加边求和的方法，既考虑发车时间具有波动性，又要尽量使上下午司机工作时间均衡，通过采用遗传算法对模型进行求解，有效增强了模型的传递性和适应性。
  问题一首先进行时间点单位统一为分钟，便于确定起点发车时间和返回终点时间。选取早高峰时间段最大发车时间间隔以达到运行所需要使用的公交车数量最少的目的。将单双班车视为同一 0-1 变量进行定量᧿述，建立发车时间点（行）与使用班车编号矩阵（列），使用标记为 1，反之为 0，矩阵的非零列向量个数即为所使用最少总公交车数。据此，本文通过发车计划矩阵的构建，建立相关的最少公交车数量模型。为了对该优化模型进行有效准确地求解，我们利用 MATLAB软件并采用算法进行遍历搜索求解，得到了最终的全局最优解，制定出使得徐州市 2 路公交车，在早高峰时段运行所需要使用的最少公交车数量的排班计划。
  问题二在问题一的基础上，制定出徐州市 2 路公交车完成一整天的运行所需要使用的最少公交车数量的排班计划，比问题一更加进一步的约束了双班车司机工作时间和极限运行班次数。已知各时间段长度，故各发车时间点即可确定，从而可计算出起终时间。为得到最少公交车总数，单双班车数和每辆车的总班次数，可通过建立全天各时间段发车时间点（行）与使用单班车编号矩阵（列）X，双班车编号矩阵（列）Y，综合得到所有班车编号矩阵（列）Z，进行求解，其非零列向量个数及各非零列向量元素之和即为待求变量。基于此模型求解得最优结果见附录表 1
  根据问题二中矩阵所得的单班车数量公式，综合考虑问题三中ᨀ到的单班车不少于 3 辆的约束即可得到满足问题三约束条件的最优解。基于此模型求解得最优结果见附录表 2
  问题四首先根据增加约束条件对问题二的模型进行改进，然后因为发车间隔的变动与最小停站时间，换班时间，双班车司机的用餐时间之间存在相互作用的关系，这些关系可能使我们要求得的最少公交车的数量发生在不同的发车间隔对应的发车时刻下的变动。为了求得在发车间隔波动的情况下的最小所需车辆数目，我们引入遗传算法，在不同的可行的发车时课表序列中进行交叉，变异，选择等操作从而得到最优的一个最少车辆数的发车时刻表序列，同时为了使算法收敛更快，我们再引入工作时间均匀度指标作为目标函数（适应度函数）的一个决定因素。基于此模型求解得最优结果见附录表 3

模型假设：

  1、假设单双班车为同一车辆类型；
  2、假设公交车按照排班计划表准时进站和出站；
  3、假设途中没有堵车和意外事故发生；
  4、假设环线为单环线，即只有一个运行方向的环线；
  5、假设每辆公交车可以运行 1 整天不需要加油；
  6、假设公交车运行单程时间已包含乘客在各站(包括起终点)的上下车时间；
  7、假设司机吃饭和换班的时间均包含最短停站时间；

问题分析：

  问题一的分析
  问题一要求根据徐州市 2 路公交车行车信息表 1，在从徐州火车站出发后经沿途站点后回到徐州火车站，即完成一次环线的情况下，制定出使得徐州市 2 路公交车，在早高峰时段运行所需要使用的最少公交车数量的排班计划。观察信息表可知，单程时间等因素的单位均为分钟，而早高峰时间段为 6:00-8:00，为便于确定起点发车时间和返回终点时间，将以小时为单位的时间段转化为以分钟为单位，即 06：00 为 0min，08：00 为 120 分钟。早高峰时间段发车时间间隔为4.0±1.0，为使运行所需要使用的公交车数量最少，选取最大发车时间间隔 5min，已知早高峰时间段共 120 分钟，故各发车时间点即可确定。单双班车除班制不同外车速、单程时间等运行条件均相同。因此确定最少公交车数量时，可将单双班车视为同一变量，建立发车时间点（行）与使用班车编号矩阵（列），使用标记为 1，反之为 0，矩阵的非零列向量个数即为所使用最少总公交车数。再依据单班车单班车通常要求在早高峰跑 2-3 个班次，一天不超过 5 个班次，的约束条件，最终确定单双班车使用方案。
  问题二的分析
  问题二要求在问题一的基础上，制定出徐州市 2 路公交车完成一整天的运行所需要使用的最少公交车数量的排班计划，比问题一更加进一步的约束了双班车的排班。对于双班车来说，要求上、下午各一个司机，上午和下午司机的工作时间尽可能均匀，并且都不超过 8 小时，每辆双班车一天运行不超过 10 个班次，由于司机工作时间均衡与司机所发车班次数有直接联系，发车班次数越多，工作时间越长，因此可将对司机工作时间尽可能均衡的要求转化为司机尽可能在各车辆每日所发班次数达到一半时进行换班，遇到不足一班次的情形进行取整运算。为得到排班计划表中起点发车时间和返回终点时间，首先将时间单位统一，得各时间段节点时间，为使运行所需要使用的公交车数量最少，选取各时间段最大发车时间间隔,又已知各时间段长度，故各发车时间点即可确定，从而可计算出起终时间。发车时间点数量为最少班次数，同时在假设不安排单班车的情况下也是最大双班车数。为得到最少公交车总数，单双班车数和每辆车的总班次数，可通过建立全天各时间段发车时间点（行）与使用单班车编号矩阵（列）X，双班车编号矩阵（列）Y，综合得到所有班车编号矩阵（列）Z，进行求解，其非零列向量个数及各非零列向量元素之和即为待求变量。
  问题三的分析
  问题三是在问题二的基础上，要求单班车不少于 3 辆，制定出徐州市 2 路公交车，完成一整天的运行所需要使用的最少公交车数量的排班计划，问题三相对于问题二的差异即为要求单班车不少于 3 辆。单班车是由同一个驾驶员驾驶的公交车。针对所有的单班车通常要求在早高峰跑 2-3 个班次，晚高峰 2-3个班次，每辆单班车一天不超过 5 个班次。早晚高峰时间段为均为 120 分钟，早高峰时间段单程时间为 80min，晚高峰时间段单程时间为 75min，也就是说，一辆单班车在早晚高峰期间均最多发车 2 次。根据问题二中矩阵所得的单班车数量公式，综合考虑问题三中ᨀ到的单班车不少于 3 辆的约束即可得到满足条件的最优解。
  问题四的分析
  该问题要求我们在考虑实际情况，即有最小的发车间隔，双班车数量限制为 19 辆和考虑双班车司机安排吃早晚饭以及换班的条件下求出最少的公交车数量。于是我们首先根据增加约束条件对问题二的模型进行改进，使得到的模型可以求解出在指定定发车时刻的情况下的最小所需车辆数目。然后，因为发车间隔的变动与最小停站时间，换班时间，双班车司机的用餐时间之间存在相互作用的关系，这些关系可能使我们要求得的最少公交车的数量发生在不同的发车间隔对应的发车时刻下的变动。为了求得在发车间隔波动的情况下的最小所需车辆数目，我们引入遗传算法，在不同的可行的发车时课表序列中进行交叉，变异，选择等操作从而得到最优的一个最少车辆数的发车时刻表序列，同时为了使算法收敛更快，我们再引入工作时间均匀度指标作为目标函数（适应度函数）的一个决定因素。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

G=zeros(16,121);
b=1;s=0;c=0;for a=1:1:16G(a,b)=1;G(1:a-1,b)=0;
G(a+1:16,b)=0;G(a,1:b-1)=0;G(a,b+1:b+16)=0;b=b+1;endfor a=1:1:16G(a,b)=1G(16:a-1,b)=0;G(a+1:16,b)=0;G(a,b:b-1)=0;G(a,b+1:b+16)=0;b=b+1;if b>25n=a;breakendendfor b=1:1:25for a=1:2s=s+G(a,b);endendif s>3for b=17:1:25for a=1:1:16if G(a,b)~=0G(a+2,b)=G(a,b);G(a,b)=0;breakendendendendb=25;for a=11:1:16 G(a,b)=1;G(16:a-1,b)=0;G(a+1:16,b)=0;G(a,b:b-1)=0;G(a,b+1:b+16)=0;b=b+1;if b>30break
endenda=3;for n=0:1:3for b=31:1:87G(a,b+14*n)=1;a=a+1;if a>=17a=3;b=31;breakendendendb=87;
for a=1:1:16G(a,b)=1;b=b+1;
end
k=0;
for b=79:1:98for a=1:2k=k+G(a,b);endendif k>3for b=87:1:103for a=1:1:16if G(a,b)~=0G(a+2,b)=G(a,b);G(a,b)=0;breakendendendend
a=3for n=0:1:2for b=103:1:122G(a,b+14*n)=1;a=a+1;if a>=17a=3;b=31;
breakendendendX=G(1:16,1:120);

G=zeros(16,121);
b=1;s=0;c=0;for a=1:1:16G(a,b)=1;G(1:a-1,b)=0;G(a+1:16,b)=0;G(a,1:b-1)=0;G(a,b+1:b+16)=0;b=b+1;endfor a=1:1:16G(a,b)=1G(16:a-1,b)=0;G(a+1:16,b)=0;G(a,b:b-1)=0;G(a,b+1:b+16)=0;b=b+1;if b>25n=a;breakendendfor b=1:1:25for a=1:3s=s+G(a,b);endendif s>3for b=17:1:25for a=1:1:16if G(a,b)~=0G(a+3,b)=G(a,b);G(a,b)=0;breakendendend
endb=25;for a=11:1:16 G(a,b)=1;G(16:a-1,b)=0;G(a+1:16,b)=0;G(a,b:b-1)=0;G(a,b+1:b+16)=0;b=b+1;if b>30breakendenda=4;for n=0:1:3for b=31:1:87G(a,b+14*n)=1;a=a+1;if a>=17a=4;b=31;breakendendendb=87;
for a=1:1:16G(a,b)=1;b=b+1;
end
k=0;
for b=79:1:98for a=1:3k=k+G(a,b);endendif k>3for b=87:1:103for a=1:1:16if G(a,b)~=0G(a+3,b)=G(a,b);G(a,b)=0;breakend
endendend
a=3for n=0:1:2for b=103:1:122G(a,b+14*n)=1;a=a+1;if a>=17a=4;b=31;breakendendendX=G(1:16,1:120);
（3）第四题：
初始种群生成函数：function [y] = creat( x )
a=[];t=0;
while t<=30r=randi([5 9],1,1);t=t+r;a(end+1)=t;
end
while t<=90r=randi([3,6],1,1);t=t+r;a(end+1)=t;
end
while t<=210r=randi([2,4],1,1);t=t+r;a(end+1)=t;
end
while t<=690r=randi([3,6],1,1);t=t+r;a(end+1)=t;
end
while t<=810r=randi([2,4],1,1);t=t+r;a(end+1)=t;
end
while t<=1065r=randi([5,8],1,1);t=t+r;a(end+1)=t;
end
y=a;
end

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可