有了投影变换的知识,我们现在可以讨论剪切空间(Clip Space)和 归一化设备坐标(NDC:Normalized Device Coordinates)。 为了理解这些主题,我们还需要深入了解齐次坐标的有趣世界。
NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎
1、透视相机回顾

请记住,透视相机被建模为称为视锥体(view frustum)的截棱锥体。
该视锥体由需要定义的几个部分组成,以便创建我们的投影矩阵:
- 近平面 - 这是通过负 z 轴(在相机空间中定义)到近剪裁平面的距离
- 远平面 - 这是通过负 z 轴(在相机空间中定义)到远剪裁平面的距离
- 视场 (fov_y) - 这是平截头体顶边和底边之间的角度。
- 纵横比 - 这是我们窗口的纵横比。
近平面和远平面之间的距离应尽可能短,以最大限度地减少深度缓冲区精度问题或避免深度冲突(z-fighting)。
让我们假设我们的场景使用透视相机来进行此计算。 请记住,透视相机建模和正交相机建模之间存在差异。
有了 gl-matrix,我们的工作就非常简单了。 我们只需要将一些参数传递给该方法,如下所示:
const aspect = this._context.canvas.width / this._context.canvas.height;const projectionMatrix = mat4.create();const fov_y = (2 * Math.PI) / 5const near = 1const far = 100mat4.perspective(projectionMatrix, fov_y, aspect, near, far);如果你有机会需要自己构建数组,那也不会太糟糕:

请注意,矩阵位置 [3][2] 处有一个 -1(假设矩阵索引为 0),因为视图空间中的 z 分量(负数)在乘以投影矩阵后成为我们的分量 w:

注意:请参阅 此图并注意相机空间和剪切空间中 z 轴方向的差异,从右手坐标系变成左手坐标系。
让我们把这个透视模型放在后袋里,继续通过在渲染管道中发挥重要作用的两个空间—剪切空间和 NDC(标准化坐标)进行顶点变换的故事。
但在我们去那里之前,我们还有一站……齐次坐标。
2、齐次坐标
啊,一周前齐次坐标吓到了我。 我很快意识到它们一点也不可怕。 实际上,它们在我们的 3D 工具箱中非常有用。
因此,为了开始我们的讨论,让我们以两周前位于三角形中的顶点为例:

为什么有四个维度? 该顶点的位置被认为是齐次坐标,因为有第四个分量 w。 我们从一开始就与他们打交道!
我们需要第四个维度有几个原因。 在下一部分中,我们将了解如何使用它们,以及 GPU 如何使用它们(从剪切空间更改为 NDC)。
齐次坐标有几个应用程序将立即对我们有用。 请注意,此列表并不完整。 齐次坐标的应用非常广泛!
2.1 投影变换
我们使用齐次坐标在射影空间中工作。
让我们看一个 2D 示例来简化这个概念:

从图中我们可以看出,w 与投影有关。 想象一下,我们将电影放映机靠近屏幕。
图像应该缩小! 此外,如果我们将电影放映机移离屏幕,图像应该会变大! 因此可以推断,w 分量影响图像相对于投影的比例。
稍后我们将看到 GPU 如何使用该值来渲染具有正确透视错觉的图像。
w 总是 = 1 吗?
我想首先要问的问题是:w = 1,这是什么意思?
正如我们刚刚看到的,w 值描述了组件相对于投影距离的比例。 因此,值为 1 意味着不会发生缩放。 因此,当 w = 1 时,它对 x、y 或 z 分量的值没有影响。
所以设置w=1是一个非常合理的初始值。 在代码中,当我们定义顶点时,我们将值设置为 1,这实际上将该组件的更新责任委托给了投影矩阵。
因此,一旦完成所有计算,w 可能不再等于 1。
2.2 3D坐标的平移
该应用程序在图形领域广泛使用。 事实上,一周前我们已经通过 4D LookAt 和 viewMatrix 矩阵看到了这一点。
通常平移向量被写为 3D 向量,并被认为是仿射变换。 此外,旋转和缩放矩阵也是 3D (3x3):

是否可以在单个矩阵中表示整个变换(平移、旋转、缩放)? 是的! 通过添加第四个分量 w,我们利用了第四维的力量:

一旦我们添加了第四个维度,我们就可以将这些矩阵相乘以构建单个矩阵,就像上周我们介绍 viewMatrix 时一样:

3、剪切空间
剪切空间(clip space) - 它是什么? 我认为这个例子可以帮助我们更清楚地看到事情:

简而言之,剪切空间被建模为棱柱,称为剪切体块(clip volume)。 如果图元的顶点在此空间之外,它们将被我们的 GPU 拒绝(剪裁)。 这样做是为了避免不必要的计算,因为无论如何我们都看不到这些顶点。
剪切体块的尺寸定义为以下边界框: (-w,-w,0), (w,w,w) ,其中w是顶点的额外维度,这使得顶点成为齐次坐标!
为了避免被 GPU 拒绝,剪切空间中的 x、y 和 z 分量必须满足以下条件:

如何进入剪切空间
我们的顶点被我们定位在剪切空间中。
为何如此? 将模型空间中的顶点转换为剪切空间所涉及的计算发生在顶点着色器中。 事实上,我们设置为输出的位置是剪切空间中的位置。
顶点着色器中通常使用的方程是:
out.position = projectionMatrix * viewMatrix * modelMatrix * inputModelSpacePosition
其中:
- inputPosition - 模型空间中的 4D 顶点位置(齐次坐标)。
- modelMatrix - 将输入顶点从模型空间转换到世界空间的 4x4 矩阵。
- viewMatrix - 4x4 视图矩阵,它将世界空间中的一个点作为输入,结果是相机空间中的一个点。
- projectionMatrix - 4x4 投影矩阵,它将相机空间中的一个点作为输入,结果是剪切空间中的投影点。
让我有点困惑的是每个顶点可以有不同的 wc 值。 因此,我们应该将剪切空间视为一个矩形棱柱,每个顶点都有其存在的自己的剪切空间。
如果三角形的顶点在同时落在剪切体块内部和外部会怎么样呢?
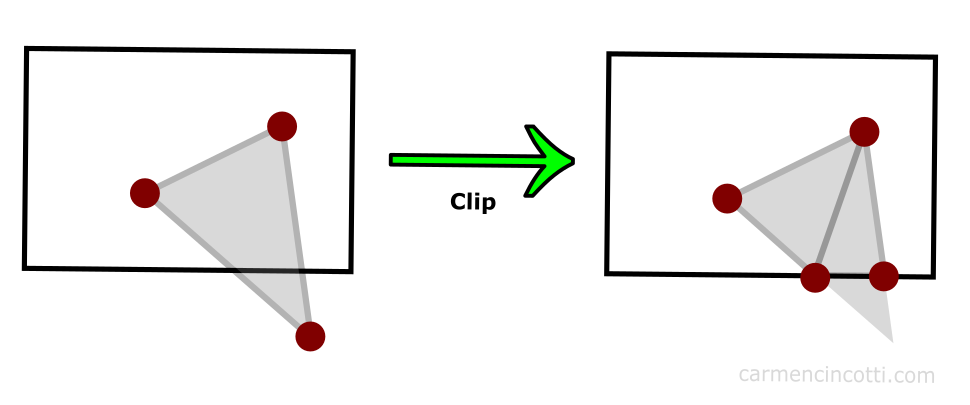
我们的 GPU 非常智能。 使用一种算法(我不会在本文中深入讨论),剪切空间之外的顶点将被裁剪,GPU 将在其位置重新绘制其他顶点,如上图所示。
结果是一个剪切基元,但仍然存在于场景中。 如果 GPU 认为有必要,这些新顶点可以创建额外的三角形。
4、NDC
裁剪剪切体块之外的顶点后,剩余顶点的位置将标准化为称为 NDC(标准化设备坐标)的通用坐标系。
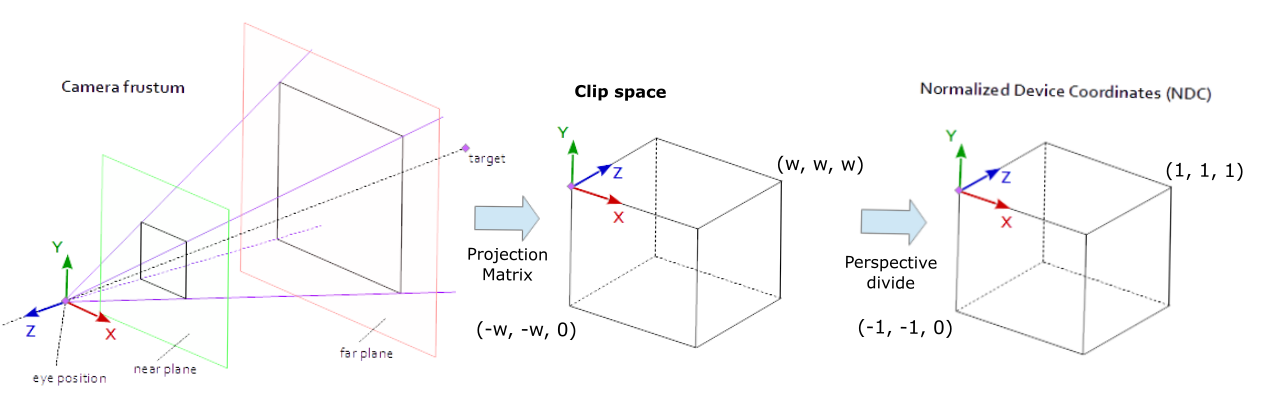
GPU 通过执行称为透视除法的操作来完成进入该坐标系的工作,其中所有顶点分量除以 w 分量:
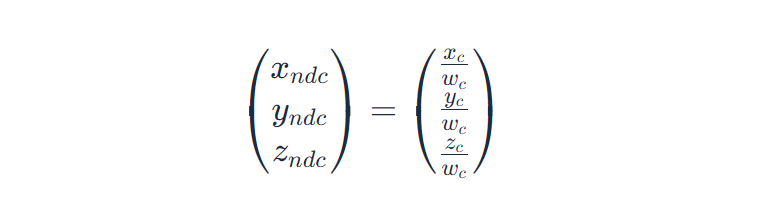
回想一下,我们刚刚剪掉了 w 维棱镜之外的所有顶点。 因此,通过将 x 和 y 分量除以 w 分量进行归一化后,我们的分量应介于 -1 和 1 之间。 对于 z 分量,标准化坐标将介于 0 和 1 之间。
⚠️ 每个图形 API 都不同,你应该查阅正在使用的图形 API 的文档,但对于 WebGPU,NDC 介于(-1, -1, 0)和(1, 1, 1)之间。
原文链接:Clip Space和NDC - BimAnt