---

Ⅰ. 前置知识

0x00 并行加法器和减法器

如果我们要对 4 位加法器和减法器进行关于二进制并行运算功能，可以通过将加法器和减法器以 N 个并行连接的方式，创建一个执行 N 位加法和减法运算的电路。

4 位二进制并行加法器

4 位二进制并行减法器

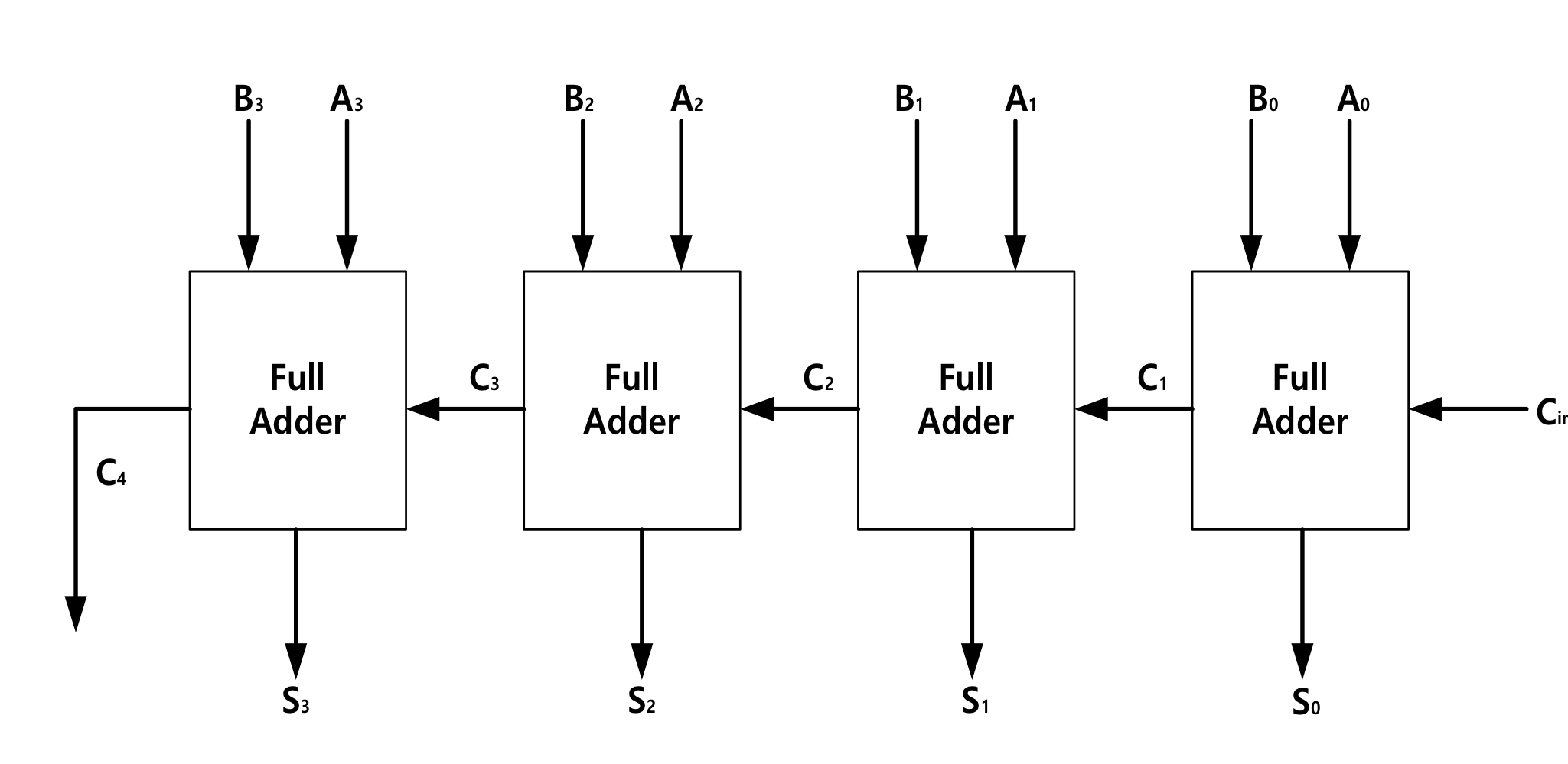
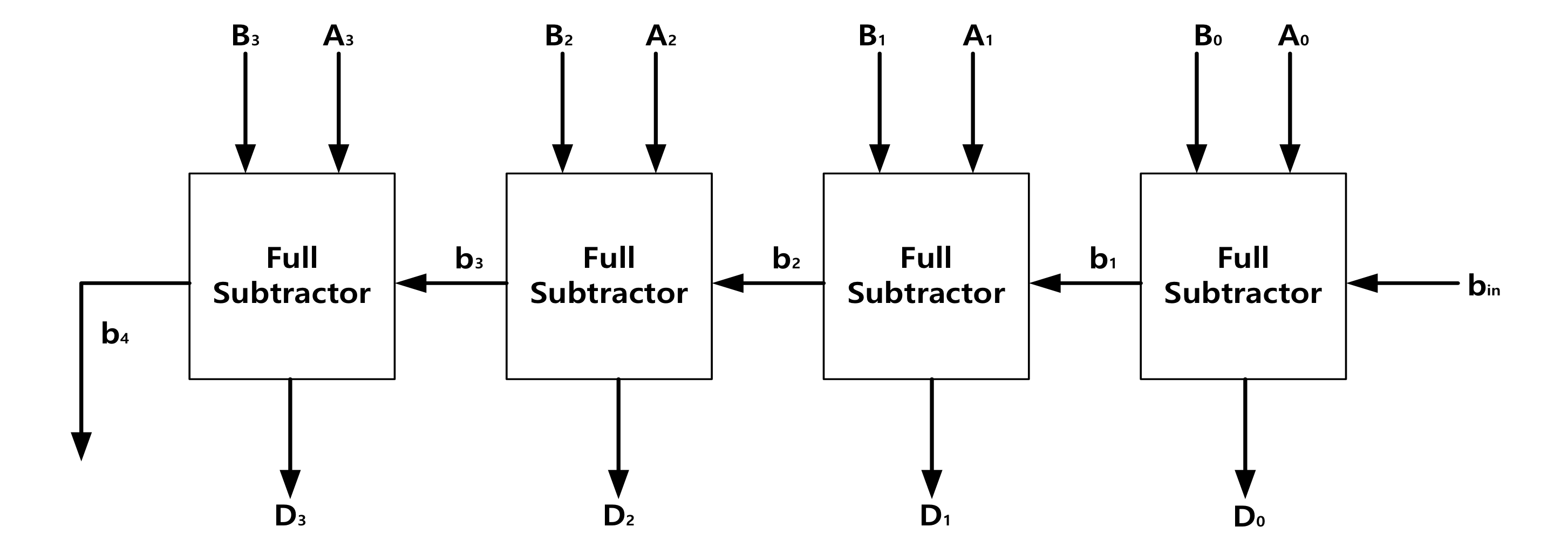
换句话说，4 位二进制并行加法器可以执行两个 4 位二进制数之间的加法运算，而 4 位二进制并行减法器可以执行两个 4 位二进制数之间的减法运算。如上图所示，4 位二进制并行加法器由四个并联的 1 位全加法器组成，而 4 位二进制并行减法器由四个并联的 1 位全减法器组成。

计算方法如下：

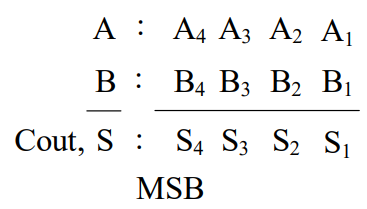
被加数和加数的各位能同时并行到达各位的输入端，而各位全加器的进位输入则是按照由低位向高位逐级串行传递的，各进位形成一个进位链。由于每一位相加的和都与本位进位输入有关，所以，最高位必须等到各低位全部相加完成并送来进位信号之后才能产生运算结果。显然，这种加法器运算速度较慢，而且位数越多，速度就越低。为了提高加法器的运算速度，必须设法减小或去除由于进位信号逐级传送所花的时间，使各位的进位直接由加数和被加数来决定，而不需依赖低位进位。根据这一思想设计的加法器称为超前进位(又称先行进位)二进制并行加法器。

0x01 超前进位（Look ahead carry）

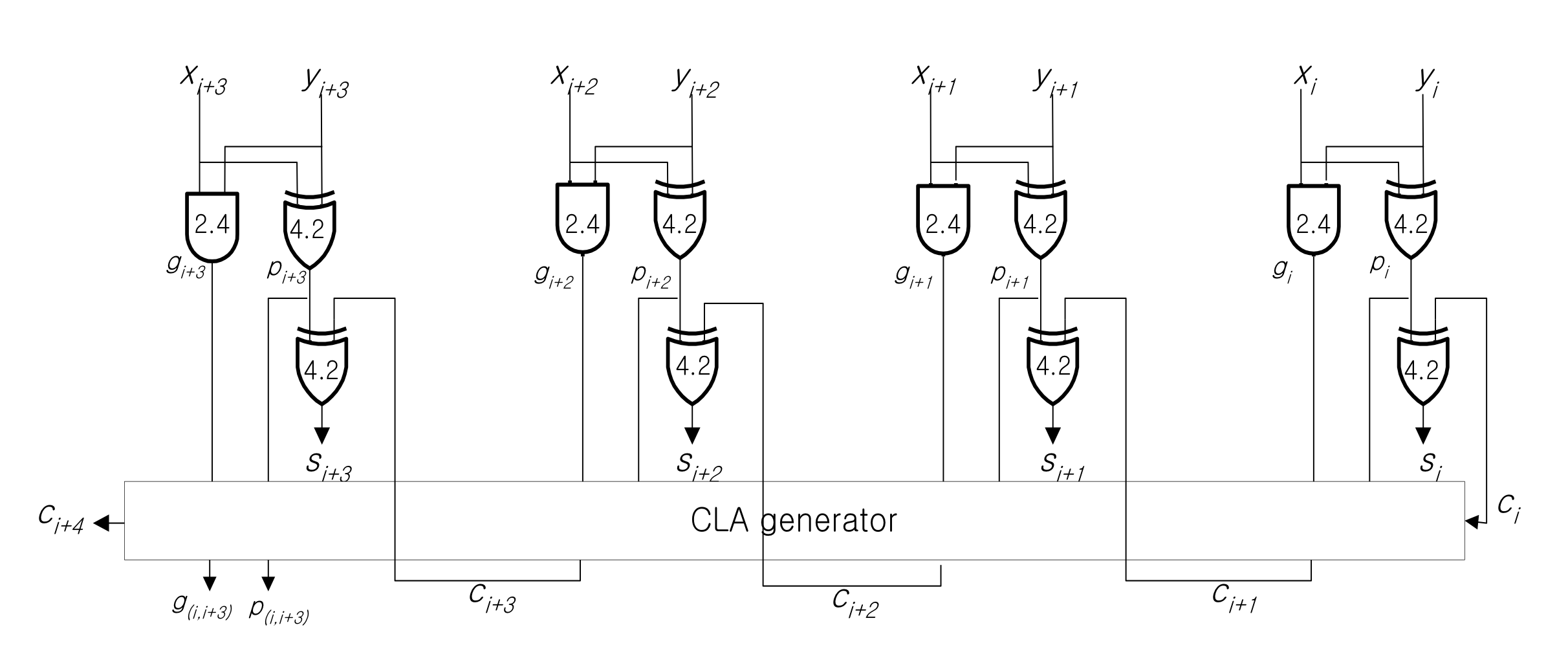
超前进位是一种用于减少纹波进位链电路运算延迟的运算方法。在多位的加法运算中，原本是将进位转移到下一位的加法运算中，并按顺序进行计算，但通过求解所有位的进位表达式并进行计算，就可以一次性计算出每一位的进位，而无需转移前一位的进位，从而减少了门通过的延迟。下图显示了使用超前进位法计算 4 位加法运算的进位。

Look Ahead Carry (4bit Adder)

4bit Look-ahead Adder

Ⅱ. 实现 4 位二进制并行加法器

0x00 实现要求

解释 4 位二进制并行加法器的结果和仿真过程

0x01 代码和仿真代码

💬 Design source：

`timescale 1ns / 1psmodule BPA(input Cin,input A0,input A1,input A2,input A3,input B0,input B1,input B2,input B3,output C1,output C2,output C3,output C4,output S0,output S1,output S2,output S3);assign S0 = (A0^B0)^Cin;
assign C1 = (Cin&(A0^B0)) | (A0&B0);assign S1 = (A1^B1)^C1;
assign C2 = (C1&(A1^B1)) | (A1&B1);assign S2 = (A2^B2)^C2;
assign C3 = (C2&(A2^B2)) | (A2&B2);assign S3 = (A3^B3)^C3;
assign C4 = (C3&(A3^B3)) | (A3&B3);endmodule

💬 Testbench：

`timescale 1ns / 1psmodule BPA_tb;
reg Cin,A0,A1,A2,A3,B0,B1,B2,B3;
wire C1,C2,C3,C4,S0,S1,S2,S3;BPA u_BPA (.Cin(Cin ),.A0(A0 ),.A1(A1 ),.A2(A2 ),.A3(A3 ),.B0(B0 ),.B1(B1 ),.B2(B2 ),.B3(B3 ),.C1(C1 ),.C2(C2 ),.C3(C3 ),.C4(C4 ),.S0(S0 ),.S1(S1 ),.S2(S2 ),.S3(S3 )
);initial beginCin = 1'b0;A0 = 1'b0;A1 = 1'b0;A2 = 1'b0;A3 = 1'b0;B0 = 1'b0;B1 = 1'b0;B2 = 1'b0;B3 = 1'b0;
endalways@(Cin or A0 or A1 or A2 or A3 or B0 or B1 or B2 or B3) beginCin <= #10 ~Cin;A0 <= #20 ~A0;A1 <= #40 ~A1;A2 <= #80 ~A2;A3 <= #160 ~A3;B0 <= #320 ~B0;B1 <= #640 ~B1;B2 <= #1280 ~B2;B3 <= #2560 ~B3;
endinitial begin#5120$finish;
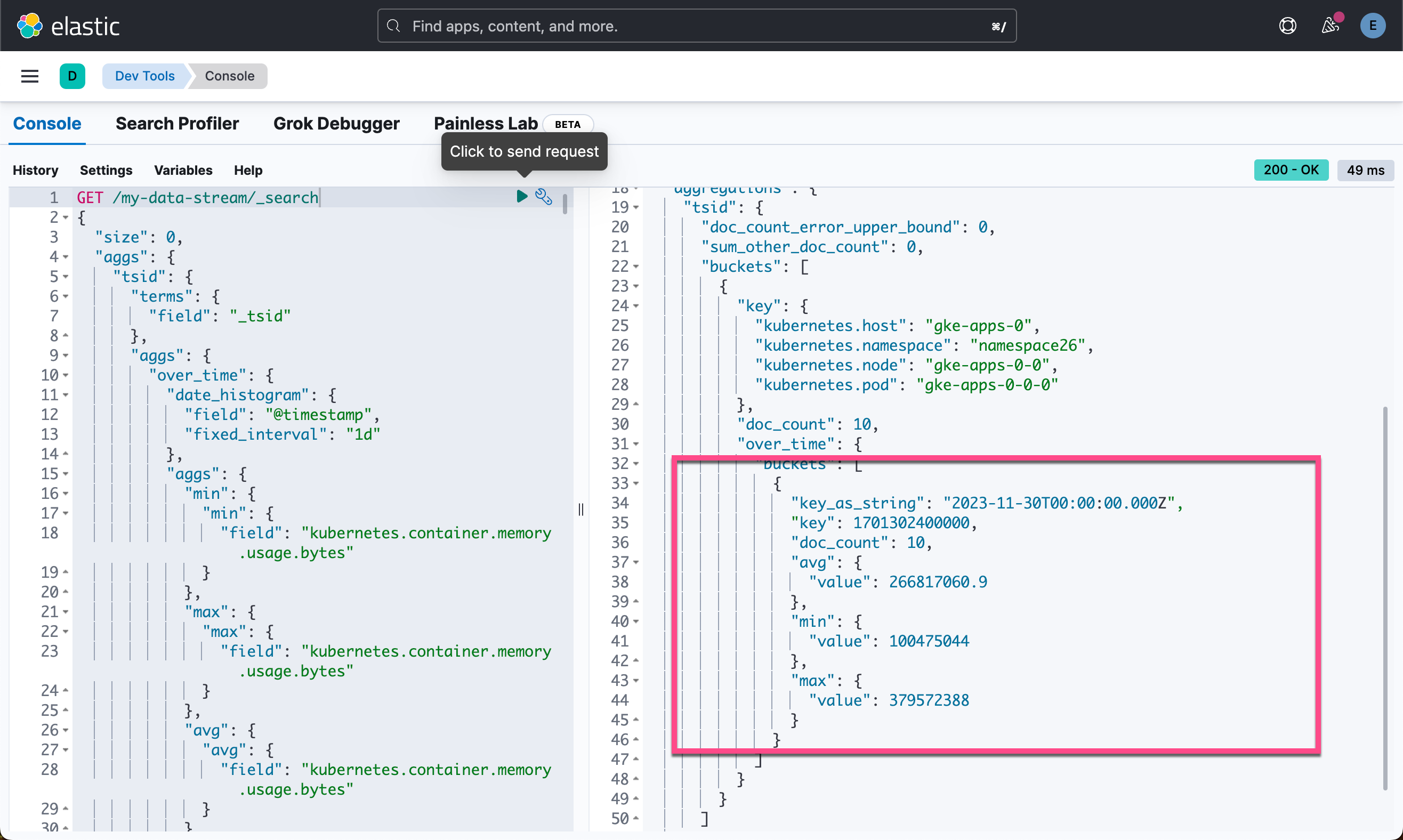
endendmodule

0x02 仿真结果

0x03 Schematic 图

📜 Schematic：

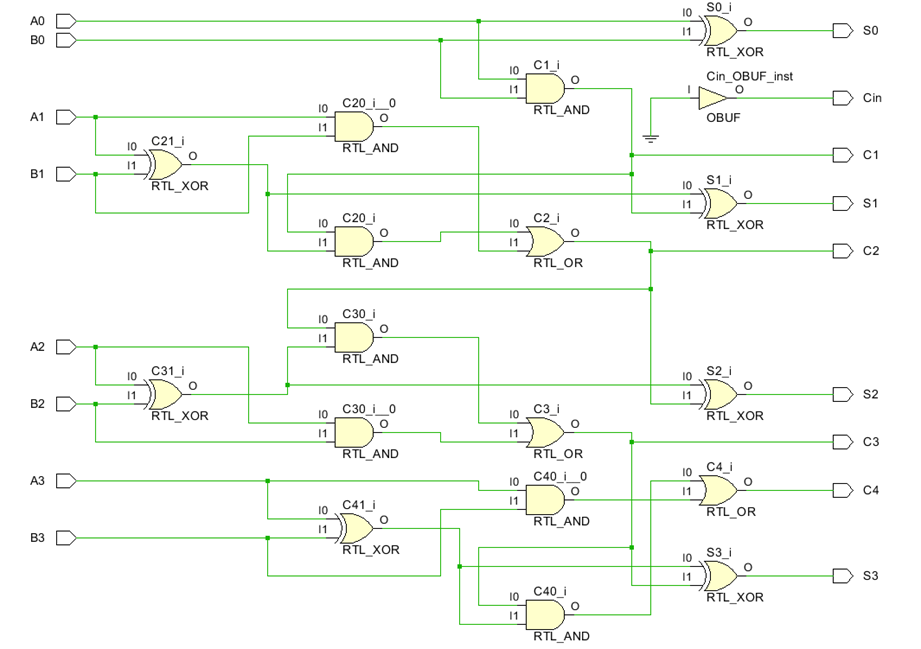
4 位二进制并行加法器是四个并行的 1 位全加法器，这意味着对每个位数执行一次加法器运算，然后将得到的和值传递给结果，并将进位值传递给下一位数加法器的进位。

Ⅲ. 实现 4 位二进制并行减法器

0x00 实现要求

解释 4 位二进制并行减法器的结果和仿真过程。

0x01 代码和仿真代码

💬 Design source：

`timescale 1ns / 1psmodule BPS(input bin,input A0,input A1,input A2,input A3,input B0,input B1,input B2,input B3,output b1,output b2,output b3,output b4,output D0,output D1,output D2,output D3);assign D0 = (A0^B0)^bin;
assign b1 = ((~(A0^B0))&bin) | ((~A0)&B0);assign D1 = (A1^B1)^b1;
assign b2 = ((~(A1^B1))&b1) | ((~A1)&B1);assign D2 = (A2^B2)^b2;
assign b3 = ((~(A2^B2))&b2) | ((~A2)&B2);assign D3 = (A3^B3)^b3;
assign b4 = ((~(A3^B3))&b3) | ((~A3)&B3);endmodule

💬 Testbench：

`timescale 1ns / 1psmodule BPS_tb;
reg bin,A0,A1,A2,A3,B0,B1,B2,B3;
wire b1,b2,b3,b4,D0,D1,D2,D3;BPS u_BPS (.A0(A0 ),.A1(A1 ),.A2(A2 ),.A3(A3 ),.B0(B0 ),.B1(B1 ),.B2(B2 ),.B3(B3 ),.bin(bin ),.b1(b1 ),.b2(b2 ),.b3(b3 ),.b4(b4 ),.D0(D0 ),.D1(D1 ),.D2(D2 ),.D3(D3 )
);initial beginbin = 1'b0;A0 = 1'b0;A1 = 1'b0;A2 = 1'b0;A3 = 1'b0;B0 = 1'b0;B1 = 1'b0;B2 = 1'b0;B3 = 1'b0;
endalways@(bin or A0 or A1 or A2 or A3 or B0 or B1 or B2 or B3) beginbin = #10 ~bin;A0 <= #20 ~A0;A1 <= #40 ~A1;A2 <= #80 ~A2;A3 <= #160 ~A3;B0 <= #320 ~B0;B1 <= #640 ~B1;B2 <= #1280 ~B2;B3 <= #2560 ~B3;
endinitial begin#5120$finish;
endendmodule

0x02 仿真结果

🚩 运行结果如下：

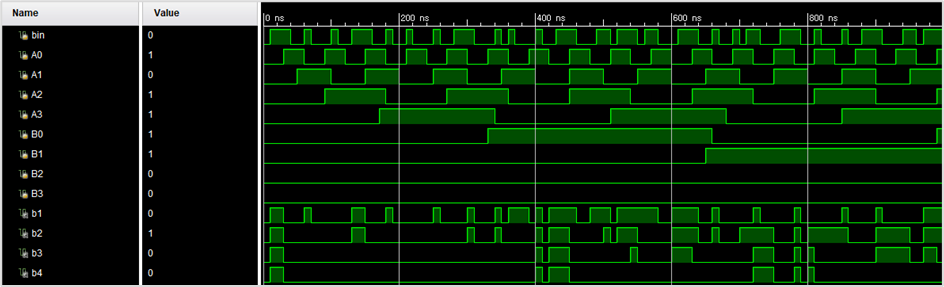
0x03 Schematic 图 

📜 Schematic：

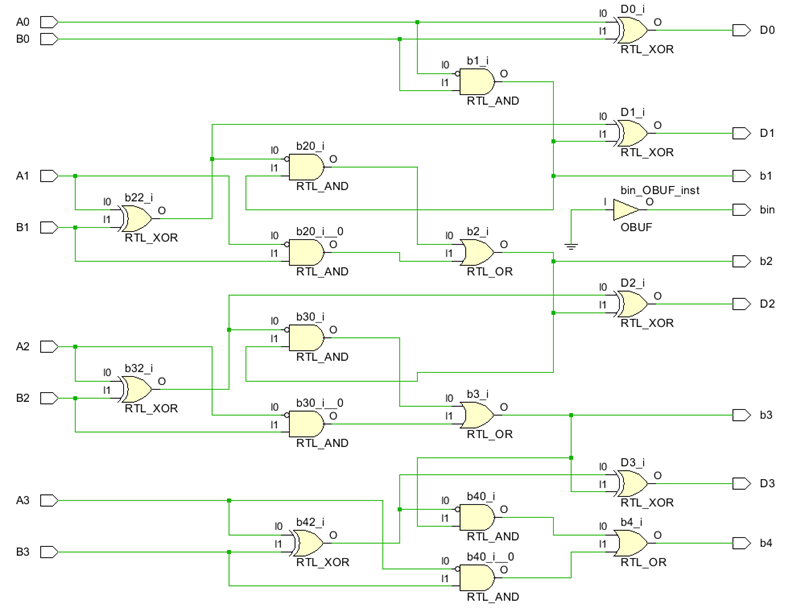
4 位二进制并行减法器是四个并行的 1 位全减法器，这意味着对每个位数执行一次减法器运算，然后将所得差值传递给结果，并将借出值传递给下一个位数减法器的借入值。

📌 [ 笔者 ]   floyd
📃 [ 更新 ]   2023.12.3
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，本人也很想知道这些错误，恳望读者批评指正！

📜 参考资料  Introduction to Logic and Computer Design, Alan Marcovitz, McGrawHill, 2008 Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . 百度百科[EB/OL]. []. https://baike.baidu.com/.