代码：

class Solution {//计算 n 每个位置上的数字的平方和public int quadraticSum(int n){int sum=0;while (n>0){int i=n%10;sum+=i*i;n/=10;}return sum;}public boolean isHappy(int n) {//慢指针int slow=n;//快指针int fast=quadraticSum(n);while (slow!=fast){slow=quadraticSum(slow);fast=quadraticSum(quadraticSum(fast));}return slow==1;}
}

题解：

        通过题意我们可以知道，要分为两种情况来进行讨论

        1.重复上述过程，最终得到的数字变为 1

        2.重复上述过程，无限循环，始终变不到 1 

        示例 1 的变化过程为：19 -> 82 -> 68 -> 100 -> 1 -> 1 -> 1（开始循环）

        示例 2 的变化过程为： 2 -> 4 -> 16 -> 37 -> 58 -> 89 -> 145 -> 42 -> 20 -> 4 (开始循环)

        实际上，当最终的数字变为 1 后，也相当于进入了循环，后面的数据都只会为 1 ，相当于进入了一个全为 1 的循环

        看下面的图像更清晰：

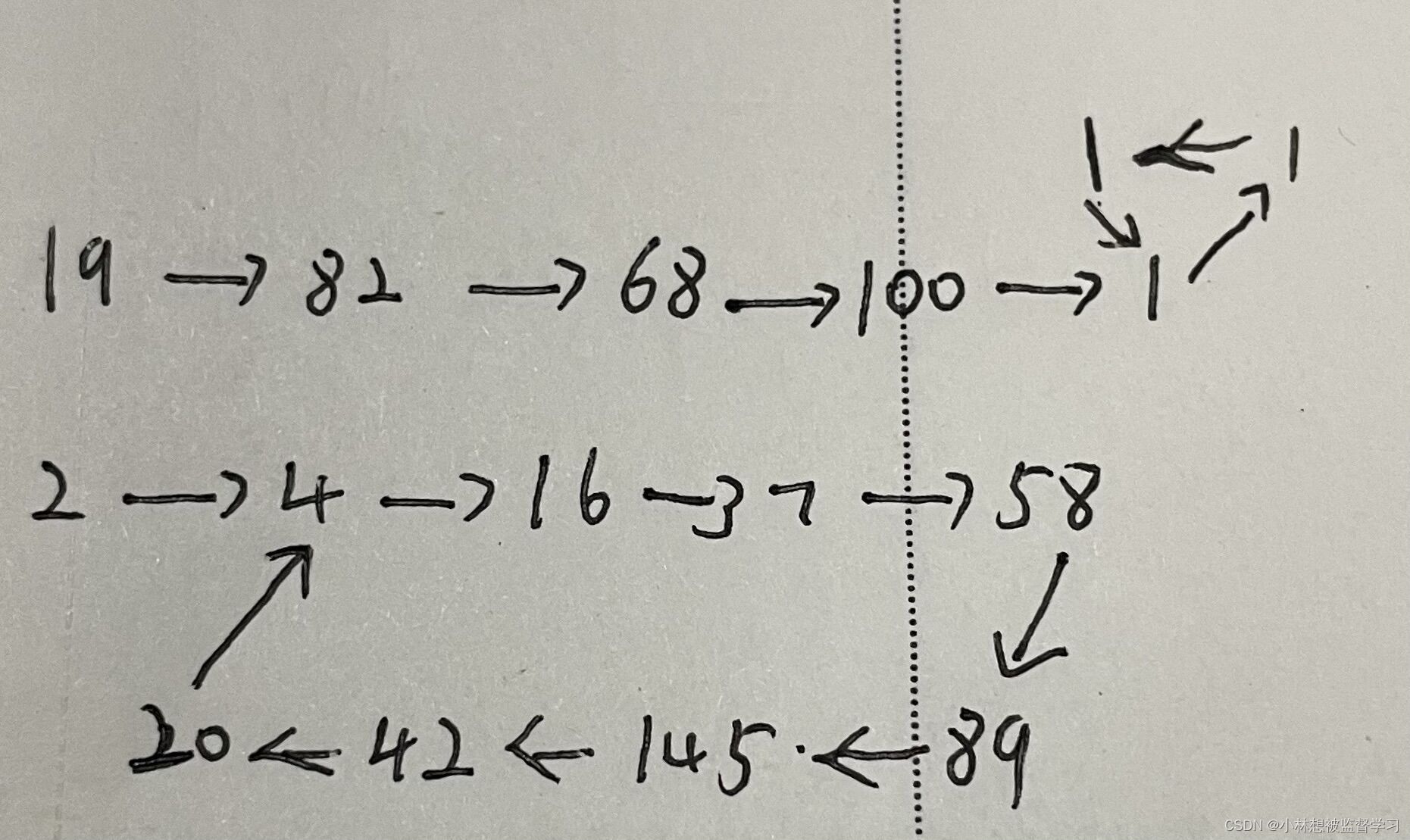
        所以我们可以得出结论，重复上述的过程肯定会产生循环，若循环中全是 1 就代表是快乐数，循环中没有 1 就不是快乐数

        我们判断一个链表里有没有环，通常是通过快慢指针的方式，原理就是，如果链表有环，快慢指针肯定就会相遇，根据这个原理，我们可以通过快慢指针去获取环中的数据，这样就能判断该数是否是快乐数了

        可能有同学会迷惑，我们的参数不是一个数吗，怎么会有链表这样的数据结构呢？如上图，我们可以将数的变化过程看作是一个遍历链表的过程，slow 慢指针一个循环变换一次数据，fast 快指针一个循环变换两次数据，当 slow 慢指针的值和 fast 快指针的值相等时，就相当于指向了环中的一个数据