题目描述

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

样例输入

示例 1：

输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

输入：nums = [4,4,3,2,1]
输出：[[4,4]]

提示：

• 1 <= nums.length <= 15
• -100 <= nums[i] <= 100

题解

如图所示，本题在使用回溯法时，需要解决以下两个问题：

（回溯法的使用详解见：组合（回溯+剪枝、图解）-CSDN博客）

• 如何判断序列递增
• 回溯遍历时如何进行去重

在使用回溯法时，我们用path数组保存遍历时路径上的每一个节点，用res保存最终结果，如下：

    vector<int> path;//保存当前结果vector<vector<int>> res;//保存最终结果

去除非递增序列

使用回溯法遍历nums时，由于我们用path数组保存当前遍历结果，因此对于下一个遍历到的元素num[i]，我们只需要判断其与path数组中最后一个元素的大小。也就是说，

如果nums[i]>=path.back()，就说明如果将当前元素nums[i]加入到path数组中，序列就可以继续保持递增，那么就可以将nums[i]添加到path数组中；

否则，说明将当前元素nums[i]加入到path数组中后序列无法保持递增，就不能将nums[i]添加到path数组中

去重

由上图我们可以看到，去重是指对同一层上出现过的元素进行去重，由于按照题意我们无法对数组进行排序，因此不能使用之前使用过的去重逻辑（组合总和II（回溯、去重）-CSDN博客），需要重新设计去重方法。

假如我们现在不考虑回溯法，那么又该如何对一个有重复元素的数组nums进行去重呢？

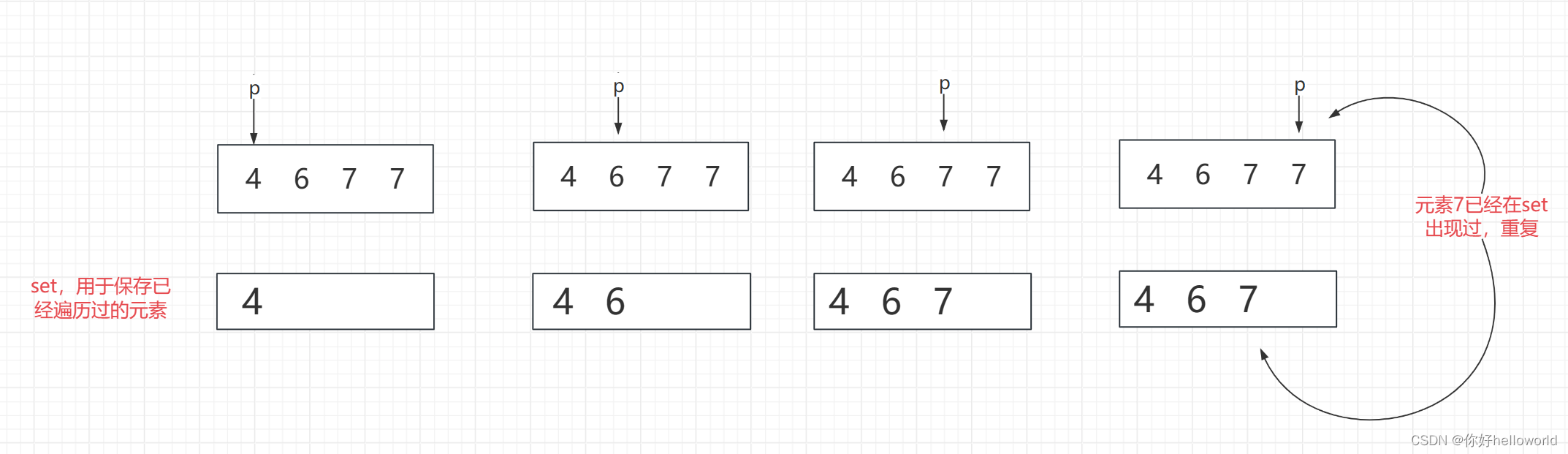
如图所示，我们用一个set集合保存已经遍历过的元素，在每次遍历新元素的时候都在set中查找当前正在遍历的元素是否在set中出现过，如果当前正在遍历的元素在set中找到了，说明该元素已经出现过，也就是与之前的元素出现了重复。

为什么用set保存已经遍历过的元素呢？因为set数据结构天然不能保存重复的元素。

故而将上述想法假如到对上图中回溯法的单层去重逻辑中，即可完成本题的去重。整体代码如下

代码

class Solution {
private:vector<int> path;vector<vector<int>> res;
public:void backing(vector<int>& nums,int startIndex){if(path.size()>1)res.push_back(path);unordered_set<int> uset;//记录本层元素是否重复for(int i=startIndex;i<nums.size();i++){/*判断当前元素1.如果nums[i]<path.back()，说明若加入元素就会使得序列非递增2.如果uset.find(nums[i])!=uset.end()，说明当前元素之前在同一层已经出现过*/if((!path.empty() && nums[i]<path.back())|| uset.find(nums[i])!=uset.end())continue;uset.insert(nums[i]);//记录当前已经使用过的元素path.push_back(nums[i]);//遍历路径上的节点backing(nums,i+1);path.pop_back();//回溯}}vector<vector<int>> findSubsequences(vector<int>& nums) {backing(nums,0);return res;}
};