题目描述：

给定圆的半径和圆心的位置，实现函数 randPoint ，在圆中产生均匀随机点。

实现 Solution 类:

Solution(double radius, double x_center, double y_center) 用圆的半径 radius 和圆心的位置 (x_center, y_center) 初始化对象
randPoint() 返回圆内的一个随机点。圆周上的一点被认为在圆内。答案作为数组返回 [x, y] 。

示例 1：
输入:
[“Solution”,“randPoint”,“randPoint”,“randPoint”]
[[1.0, 0.0, 0.0], [], [], []]
输出: [null, [-0.02493, -0.38077], [0.82314, 0.38945], [0.36572, 0.17248]]
解释:
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint ();//返回[-0.02493，-0.38077]
solution.randPoint ();//返回[0.82314,0.38945]
solution.randPoint ();//返回[0.36572,0.17248]

提示：
0 < radius <= 10⁸
-10⁷ <= x_center, y_center <= 10⁷
randPoint 最多被调用 3 * 10⁴ 次

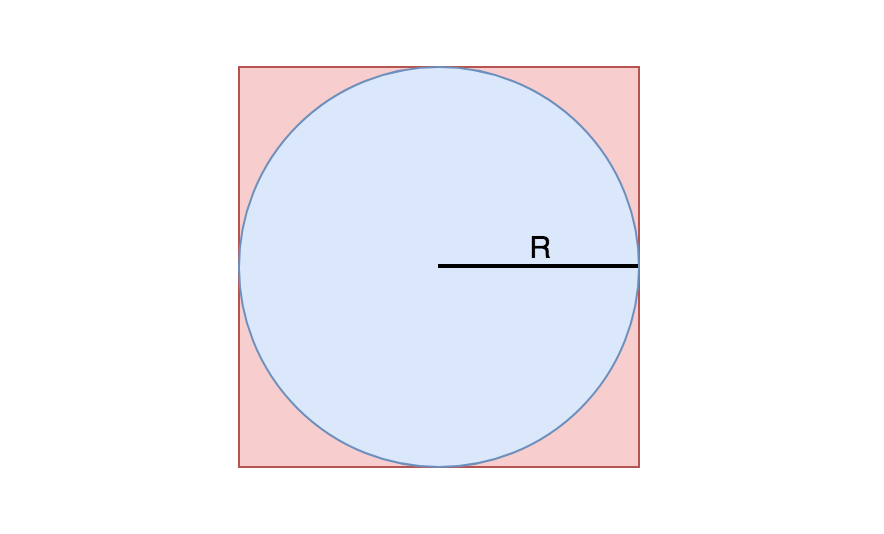
解题思路一：一个最简单的方法就是在一个正方形内生成随机采样的点，然后拒绝不在内切圆中的采样点。

class Solution:def __init__(self, radius: float, x_center: float, y_center: float):self.r = radiusself.x = x_centerself.y = y_centerdef randPoint(self) -> List[float]:while True:x, y =random.uniform(-self.r, self.r), random.uniform(-self.r, self.r)if x*x +y*y <= self.r * self.r:return [self.x + x, self.y + y]# Your Solution object will be instantiated and called as such:
# obj = Solution(radius, x_center, y_center)
# param_1 = obj.randPoint()

调用的期望次数是圆的面积除以正方形的面积。即(2R)²/πR²约等于0.785即O(1)，也就是时间复杂度。
时间复杂度：O(1)
空间复杂度：O(1)

解题思路二：具体思想是先生成一个0到r的随机数len，然后生成一个随机的角度来生成对应的坐标。但是这样并不是等概率的，因为例如 len 有 $\frac{1}{2}$的概率取到小于等于$\frac{r}{2}$的值，而半径为$\frac{r}{2}$扫过的面积仅为总面积的$\frac{1}{4}$，因此我们的 len 不能直接在[0, r]范围内随机，为了消除这种一维转圆导致的「等概率」失效，我们可以从[0, r²]内随机再开平方，从而确保距离与面积比例一致。

class Solution:def __init__(self, radius: float, x_center: float, y_center: float):self.r = radiusself.x = x_centerself.y = y_centerdef randPoint(self) -> List[float]:u, theta = random.random(), random.random()*2*math.pir = sqrt(u)return [self.x + r*math.cos(theta)*self.r, self.y + + r*math.sin(theta)*self.r]

时间复杂度：O(1)
空间复杂度：O(1)

解题思路三：0