目录
1 数据处理
1.1 数据集简介
1.2 导入库文件
1.3 数据集处理
1.4 训练数据构造
2 模型训练与预测
2.1 模型训练
2.2 模型多步预测
2.3 预测可视化
1 数据处理
1.1 数据集简介
实验数据集采用数据集7:常州普利司通光伏数据集(下载链接),包括数据集包括时间、场站名称、辐照强度(Wh/㎡)、 环境温度(℃)、全场功率(kW)等5个特征,时间间隔5min。(注意:辐照强度(Wh/㎡)、 环境温度(℃)、全场功率(kW)特征名前有个空格)
# 可视化数据
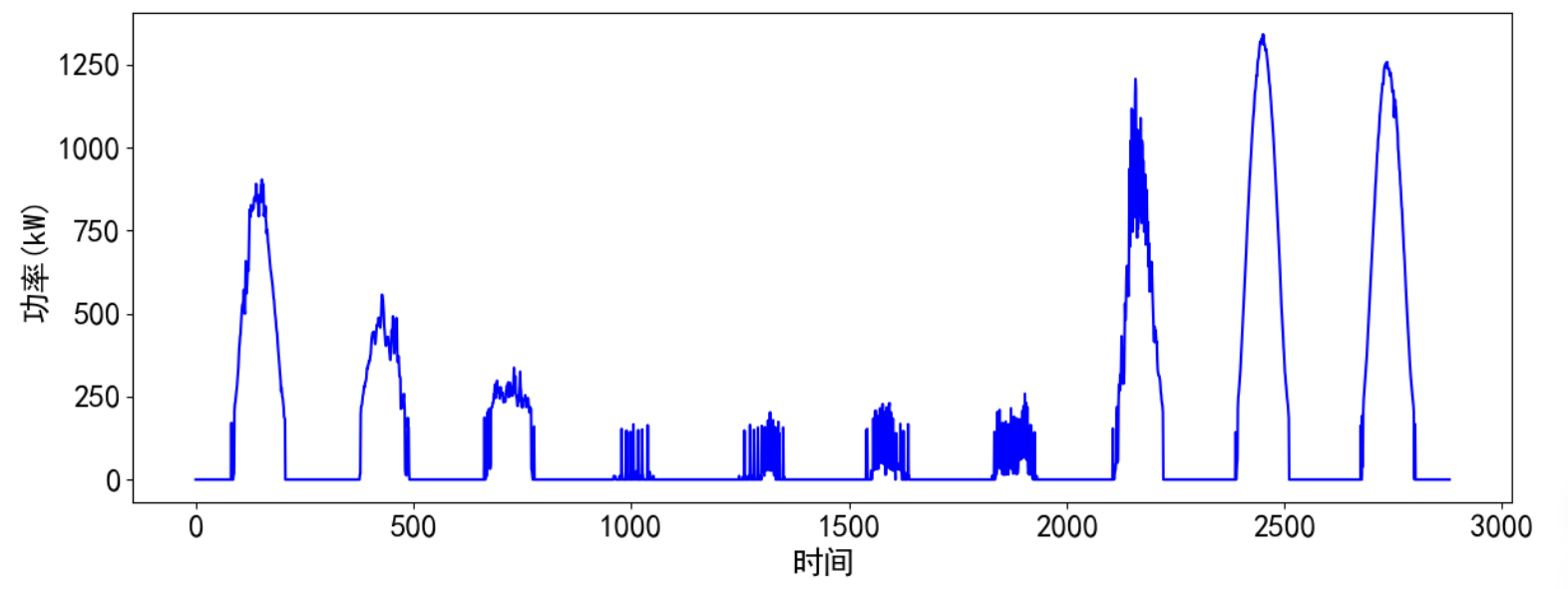
def visualize_data(data, row, col):cycol = cycle('bgrcmk')cols = list(data.columns)fig, axes = plt.subplots(row, col, figsize=(16, 4))fig.tight_layout()if row == 1 and col == 1: # 处理只有1行1列的情况axes = [axes] # 转换为列表,方便统一处理for i, ax in enumerate(axes.flat):if i < len(cols):ax.plot(data.iloc[:,i], c=next(cycol))ax.set_title(cols[i])else:ax.axis('off') # 如果数据列数小于子图数量,关闭多余的子图plt.subplots_adjust(hspace=0.5)plt.show()visualize_data(data, 1, 3)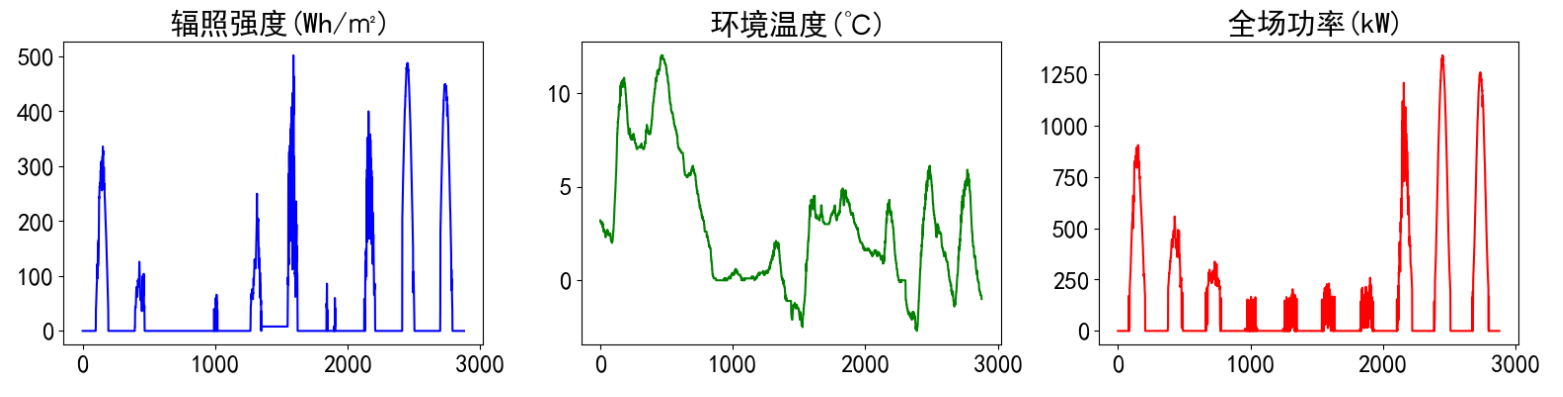
单独查看部分光伏发电功率数据,发现有较强的规律性。
1.2 导入库文件
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
import tensorflow as tffrom tensorflow.keras.models import Sequential
from tensorflow.keras.layers import GRU, Dropout, Dense
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from itertools import cycleimport joblib
import datetimeplt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams.update({'font.size':18})1.3 数据集处理
首先检查数据的缺失值情况,通过统计数据可以看到,存在少量缺失值。
# 缺失值统计
data.isnull().sum()
时间、场站名称无效信息可以删除,辐照强度(Wh/㎡)、 环境温度(℃)、全场功率(kW)存在少量缺失值,用前后项值进行填充(这里缺失值填充可根据自己的方法处理)。
# 特征删除和缺失值填充
data.drop(['时间','场站名称'], axis=1, inplace=True)
data = data.fillna(method='ffill')
# 调整列位置
data = data[[' 辐照强度(Wh/㎡)', ' 环境温度(℃)', ' 全场功率(kW)']]然后将数据转化为数值类型便于后续处理。
dataf = data.values1.4 训练数据构造
计划预测后1/4天的数据96个,将要预测的数据保留(也就是未来未知的数据),单独提取出前面训练的数据(也就是历史数据),并对数据集进行滚动划分,特征和标签分开划分。

#构造数据集
def create_dataset(datasetx,datasety,timesteps=36,predict_size=6):datax=[]#构造xdatay=[]#构造yfor each in range(len(datasetx)-timesteps - predict_steps):x = datasetx[each:each+timesteps,0:6]y = datasety[each+timesteps:each+timesteps+predict_steps,0]datax.append(x)datay.append(y)return datax, datay#np.array(datax),np.array(datay)接着设置预测的时间步、每次预测的步长、最后总的预测步长,参数可以根据需要更改。跟前面文章不同的是,这里没有滚动预测,因为没有持续的特征传入,在实际运用有特征传入时可以滚动预测。
timesteps = 96*5 #构造x,为96*5个数据,表示每次用前5/4天的数据作为一段
predict_steps = 96 #构造y,为96个数据,表示用后1/4的数据作为一段
length = 96 #预测多步,预测96个数据据接着对数据进行归一化处理,特征和标签分开划分,并分开进行归一化处理。
# 特征和标签分开划分
datafx = dataf[:,:-1]
datafy = dataf[:,-1].reshape(dataf.shape[0],1)# 分开进行归一化处理
scaler1 = MinMaxScaler(feature_range=(0,1))
scaler2 = MinMaxScaler(feature_range=(0,1))
datafx = scaler1.fit_transform(datafx)
datafy = scaler2.fit_transform(datafy)最后对这行数据集进行划分,并将数据变换为满足模型格式要求的数据。
trainx, trainy = create_dataset(datafx[:-predict_steps*6,:],datafy[:-predict_steps*6],timesteps, predict_steps)
trainx = np.array(trainx)
trainy = np.array(trainy)2 模型训练与预测
2.1 模型训练
首先搭建模型的常规操作,然后使用训练数据trainx和trainy进行训练,进行20个epochs的训练,每个batch包含128个样本。此时input_shape划分数据集时每个x的形状。(建议使用GPU进行训练,因为本人电脑性能有限,建议增加epochs值)
# Define the GPU device
physical_devices = tf.config.list_physical_devices('GPU')
if physical_devices:tf.config.experimental.set_memory_growth(physical_devices[0], True)# GRU training
start_time = datetime.datetime.now()
model = Sequential()
model.add(GRU(128, input_shape=(timesteps, trainx.shape[2]), return_sequences=True))
model.add(Dropout(0.5))
model.add(GRU(128, return_sequences=True))
model.add(GRU(64, return_sequences=False))
model.add(Dense(predict_steps))
model.compile(loss="mean_squared_error", optimizer="adam")
model.fit(trainx, trainy, epochs=20, batch_size=128)
end_time = datetime.datetime.now()
running_time = end_time - start_time# 保存模型
model.save('gru_model.h5')2.2 模型多步预测
下面介绍文章中最重要,也是真正没有未来特征的情况下预测未来标签的方法。整体的思路也就是,前面通过前96*5个数据训练后面的96个未来数据,预测时取出前96*5个数据预测未来的96个未来数据。这里与单变量预测不同,没有进行滚动预测,因为单变量预测的结果可以作为历史数据进行滚动,这里多变量只产生了预测值,并没有预测标签,不能进行滚动预测,在实际有数据源源不断时可以采用滚动预测。(里面的数据可以根据需求进行更改)

首先提取需要带入模型的数据,也就是预测前的96*5行特征和后96个标签。
y_true = dataf[-96:,-1]
predictx = datafx[-96*6:-96]然后加载训练好的模型:
# 加载模型
from tensorflow.keras.models import load_model
model = load_model('gru_model.h5')2.3 预测可视化
预测并计算误差,并进行可视化,将这些步骤封装为函数。
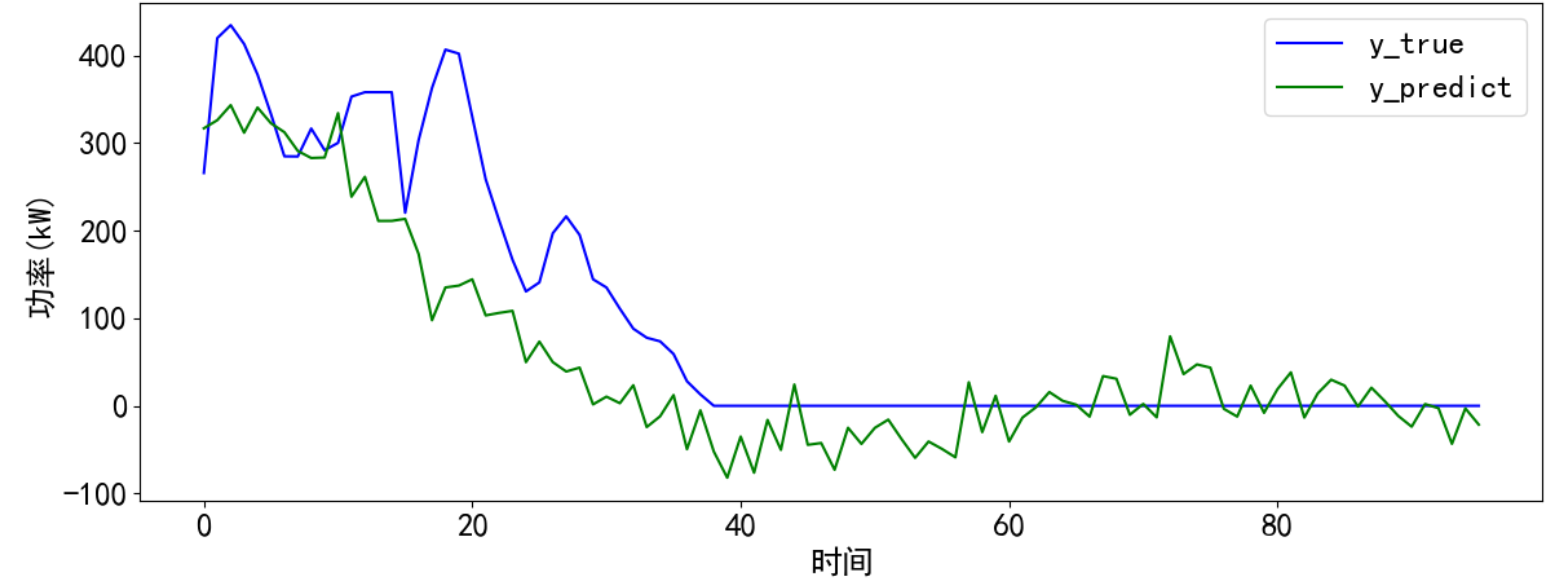
def predict_and_plot(x, y_true, model, scaler, timesteps):# 变换输入x格式,适应LSTM模型predict_x = np.reshape(x, (1, timesteps, 2)) # 预测predict_y = model.predict(predict_x)predict_y = scaler.inverse_transform(predict_y)y_predict = []y_predict.extend(predict_y[0])# 计算误差train_score = np.sqrt(mean_squared_error(y_true, y_predict))print("train score RMSE: %.2f" % train_score)# 预测结果可视化cycol = cycle('bgrcmk')plt.figure(dpi=100, figsize=(14, 5))plt.plot(y_true, c=next(cycol), markevery=5)plt.plot(y_predict, c=next(cycol), markevery=5)plt.legend(['y_true', 'y_predict'])plt.xlabel('时间')plt.ylabel('功率(kW)')plt.show()return y_predict最后运行结果,发现预测的效果大致捕捉了趋势,预测值存在一定程度的波动,也出现功率值小于0的情况,可以自行处理。
y_predict = predict_and_plot(predictx1, y_true1, model, scaler2, timesteps)