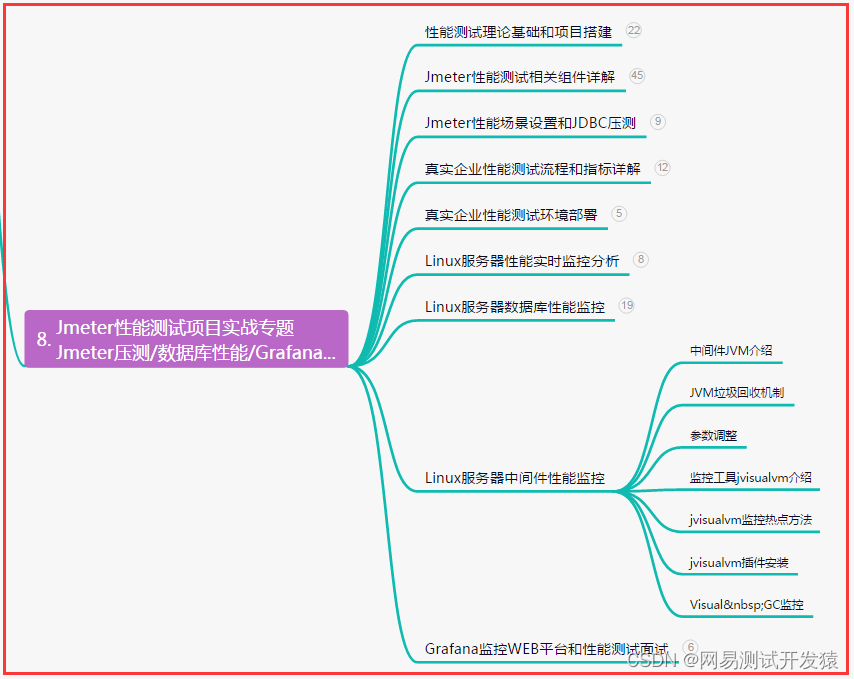
在以前的FISCO环境中仿真拜占庭节点攻击区块链网络。该环境共有100个节点,采用PBFT作为共识机制,节点编号分别为:Node0,Node,… ,Node99。这100个节点的前2010区块完全相同,自区块2011开始分叉。
(1)1个拜占庭节点:Node0
Node0 区块长度2020,Node1 - Node99区块长度2030。
在Node0上发起交易,Node0区块同步失败。
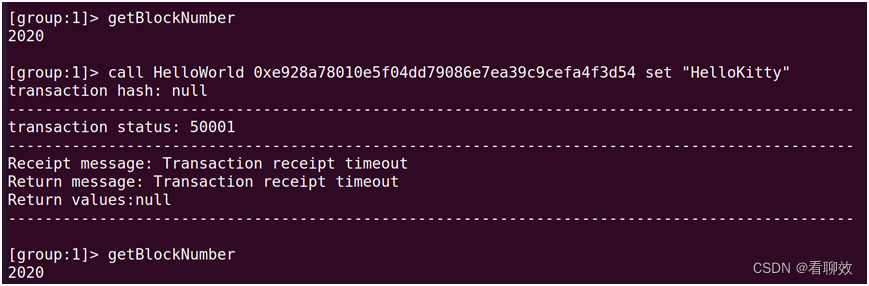
在其他节点上交易成功,区块同步成功。

这说明:100个节点中Node0被抛弃,99个节点仍能PBFT共识成功。
反过来,在Node99节点上发起同样的交易,成功。
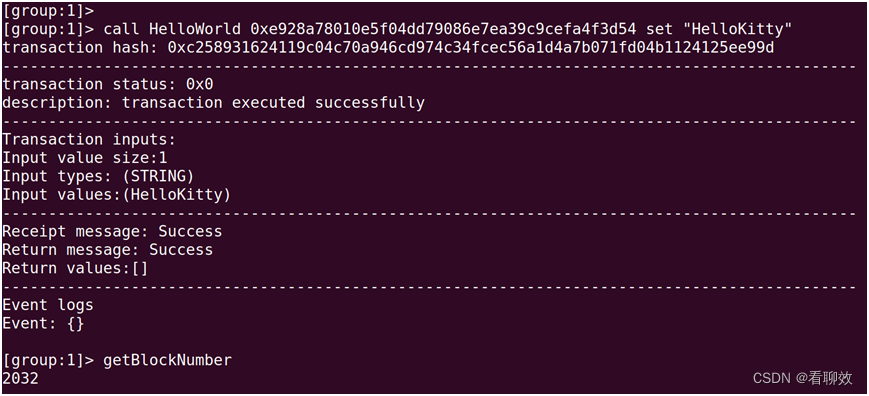
但Node0节点的区块未更新,节点被抛弃。

(2)33个拜占庭节点:Node0 – Node32
Node0 – Node32 区块长度2020,Node33 - Node99区块长度2030
在Node0上发起交易,交易失败,区块长度未变。
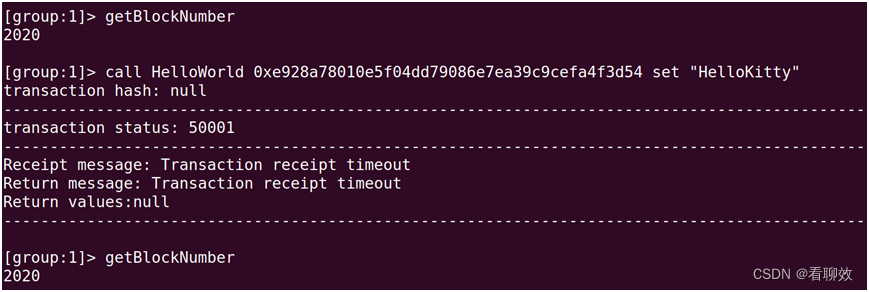
Node99节点的区块长度也未变,说明交易失败。

反过来,在Node99节点上发起同样的交易,同样失败。
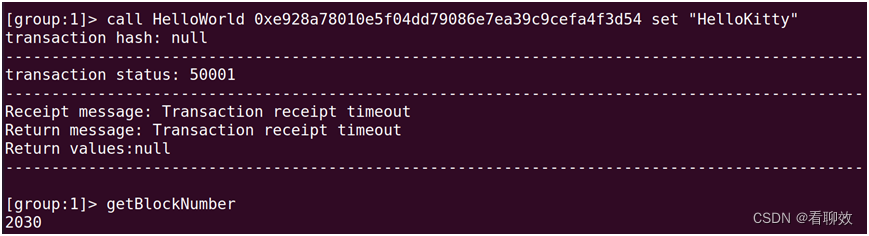
Node0节点的区块长度也未变,交易彻底失败。

此时,整个区块链失去共识能力。
(3)32个拜占庭节点:Node0 – Node31
Node0 – Node31 区块长度2020,Node32 - Node99区块长度2030
在Node0上发起交易,Node0的区块长度未变。
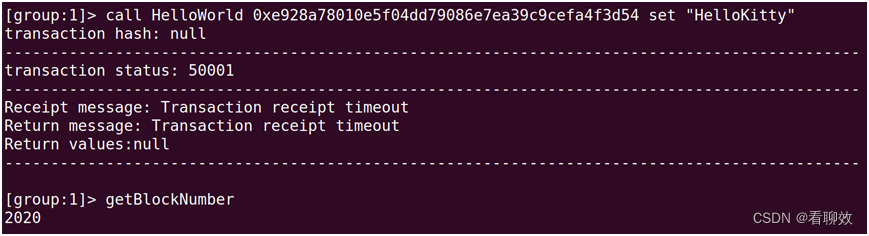
但在Node99上区块长度加1,说明交易成功。

相同地,在Node99上发起交易,交易成功,区块长度加1.
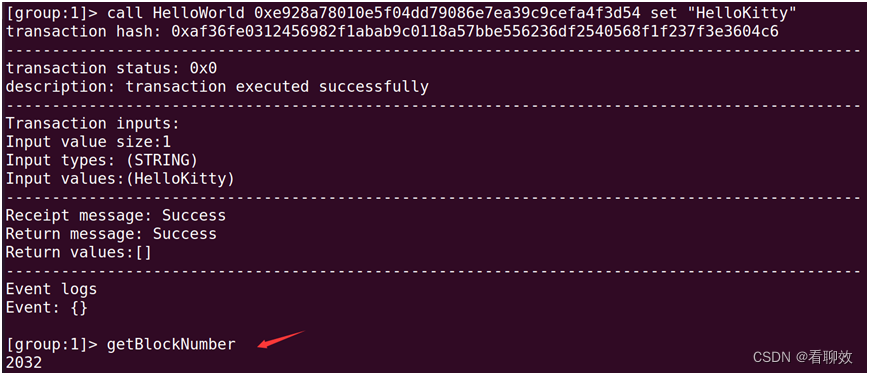
然而,Node0节点的区块长度未变。










![[idea]idea连接clickhouse23.6.2.18](https://img-blog.csdnimg.cn/direct/6d7834e2081648d6a6a40642516d157e.png)