1. 蒙特霍尔问题
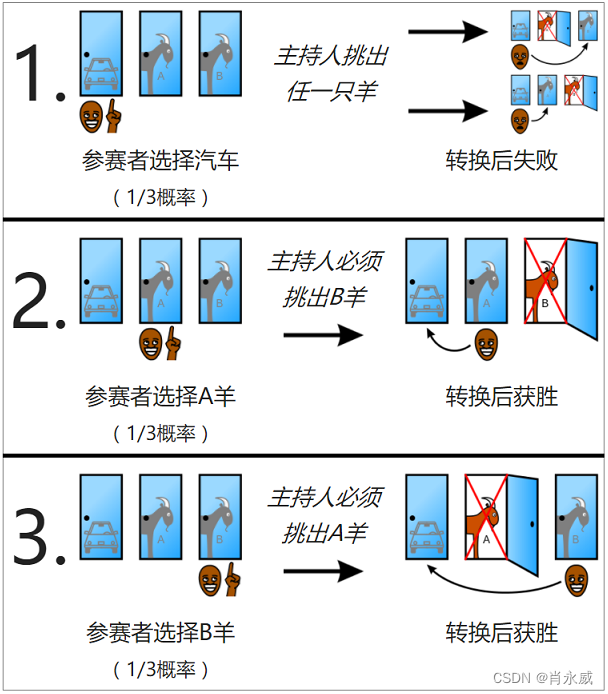
有一个美国电视游戏节目叫做“Let’s Make a Deal”,游戏中参赛者将面对3扇关闭的门,其中一扇门背后有一辆汽车,另外两扇门后是山羊,参赛者如果能猜中哪一扇门后是汽车,就可以得到它。
通常,当参赛者选定了一扇门时,节目的主持人蒙特霍尔(Monty Hall)会打开剩余两扇门中的一扇(主持人知道门后是什么),让你看到门后的山羊,此时会询问参赛者是否换门,大部分参赛者认为这时关闭的两扇门中奖的概率是一样的,即都是1/2,通常他们不会改变他们第一次的选择。您是否觉得两个问题几乎一样呢?

网上说法很多,我们以标准版:主持人事先知道答案,会打开一扇你没选择的门,且其背后一定是羊为条件,其他情况不在此过多的扩展。如下图所示剩下两个门供你选择。
| 序号 | 参赛者初选 | 再选择换门 | 结果 |
|---|---|---|---|
| 1 | 有车门 | 有羊门 | 失败 |
| 2 | 有羊门A | 有车门 | 获胜 |
| 3 | 有羊门B | 有车门 | 获胜 |
参赛者最初选择时有1/3的相同概率选择汽车、羊A和羊B,再选择转换后的获胜概率为2/3。
2. 数学解释
蒙特霍尔问题的数学证明可以通过贝叶斯定理来完成。我们可以先了解一些定义。
2.1. 贝叶斯定理
2.1.1. 独立事件概率
我们设定事件 A A A的概率为 P ( A ) P(A) P(A),事件 B B B的概率是 P ( B ) P(B) P(B),且事件 A A A和事件 B B B是相互独立的。
则事件 A A A和事件 B B B同时发生的概率,满足如下公式:
P ( A B ) = P ( B A ) = P ( A ) P ( B ) P(AB)=P(BA)=P(A)P(B) P(AB)=P(BA)=P(A)P(B)
2.1.2. 条件概率
条件概率是在某种条件下,某个事件发生的概率,展示了事件之间的内在联系和影响。
我们来看两种条件概率的简单表述。
1.事件 A A A发生之后,事件 B B B发生的概率,可以记做 P ( B ∣ A ) P(B|A) P(B∣A),此时满足公式:
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB),即 A A A 和 B B B 同时发生的概率除以 A A A 发生的概率。
等价于 P ( A B ) = P ( B ∣ A ) P ( A ) P(AB)=P(B|A)P(A) P(AB)=P(B∣A)P(A)
2.事件 B B B发生之后,事件 A A A发生的概率,可以记做 P ( A ∣ B ) P(A|B) P(A∣B),此时满足公式:
P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B)=\frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)
等价于 P ( A B ) = P ( A ∣ B ) P ( B ) P(AB)=P(A|B)P(B) P(AB)=P(A∣B)P(B)
3.综合这两种条件事件,可以得到公式:
P ( A B ) = P ( A ∣ B ) P ( B ) = P ( B ∣ A ) P ( A ) P(AB)=P(A|B)P(B) = P(B|A)P(A) P(AB)=P(A∣B)P(B)=P(B∣A)P(A)
2.1.3. 贝叶斯公式
我们综合计算得到一个公式:
P ( A ∣ B ) P ( B ) = P ( B ∣ A ) P ( A ) P(A|B)P(B) = P(B|A)P(A) P(A∣B)P(B)=P(B∣A)P(A)
这个公式做一个变形可以得到贝叶斯公式:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
2.1.4. 先验概率和后验概率
在贝叶斯公式中,还隐含着一些术语:
- P ( A ) P(A) P(A)是 A A A的先验概率或边缘概率,它不考虑任何 B B B方面的因素。
- P ( A ∣ B ) P(A|B) P(A∣B)是 B B B发生后 A A A的条件概率,由于得自 B B B的取值被称作 A A A的后验概率。
2.2. 贝叶斯定理解释蒙特霍尔问题
前面我们提到了,关键条件在于主持人选择B门后是无车的,这个事件对于已作出选择的参赛者来说是否有影响呢?后验概率是否产生了影响,我们来推导一下:
- 设定A、B、C门后有汽车分别记为事件 A A A、 B B B、 C C C,
则 P ( A ) = P ( B ) = P ( C ) = 1 3 P(A)=P(B)=P(C)=\frac{1}{3} P(A)=P(B)=P(C)=31。 - 设定参赛者选择了A门,由于主持人默认需要选择没有汽车的门,因此参赛者的选择影响了主持人的选择。
- 设定主持人选择了B门且没有汽车,记为事件 D D D,
则 P ( D ∣ A ) = 1 2 P(D|A)=\frac{1}{2} P(D∣A)=21(因为如果选手最初选择了A门,主持人可以选择打开B或C,而汽车在B或C的概率相等)
P ( D ∣ B ) = 0 P(D|B)=0 P(D∣B)=0(因为主持人不会打开选择的门)
P ( D ∣ C ) = 1 P(D|C)=1 P(D∣C)=1(因为如果选手最初选择了C门,主持人只能选择打开B门)。 - 在主持人选择B门无汽车后,参赛者选择A门有车的概率为 P ( A ∣ D ) P(A|D) P(A∣D),即事件 D D D发生后事件 A A A的概率,由贝叶斯公式得:
P ( A ∣ D ) = P ( D ∣ A ) P ( A ) P ( D ) P(A|D)=\frac{P(D|A)P(A)}{P(D)} P(A∣D)=P(D)P(D∣A)P(A) - 通过前面的分析,我们只需要求 P ( D ∣ A ) P(D|A) P(D∣A)、 P ( A ) P(A) P(A)、 P ( D ) P(D) P(D)三个元素即可。
- P ( D ∣ A ) P(D|A) P(D∣A)表示A门有汽车的情况下,主持人选择B门的概率,其为 1 2 \frac{1}{2} 21;
- P ( A ) P(A) P(A)表示A门有汽车的概率,其为 1 3 \frac{1}{3} 31;
- P ( D ) P(D) P(D)可以从全概率公式求得,其为 1 2 \frac{1}{2} 21:
P ( D ) = P ( D ∣ A ) P ( A ) + P ( D ∣ B ) P ( B ) + P ( D ∣ C ) P ( C ) P(D)=P(D|A)P(A)+P(D|B)P(B)+P(D|C)P(C) P(D)=P(D∣A)P(A)+P(D∣B)P(B)+P(D∣C)P(C)
P ( D ) = 1 2 × 1 3 + 0 × 1 3 + 1 × 1 3 = 1 2 P(D)=\frac{1}{2}\times\frac{1}{3}+0\times\frac{1}{3}+1\times\frac{1}{3}=\frac{1}{2} P(D)=21×31+0×31+1×31=21
- 综上得到:
P ( A ∣ D ) = P ( D ∣ A ) P ( A ) P ( D ) = 1 2 × 1 3 2 = 1 3 P(A|D)=\frac{P(D|A)P(A)}{P(D)}=\frac{\frac{1}{2}\times\frac{1}{3}}{2}=\frac{1}{3} P(A∣D)=P(D)P(D∣A)P(A)=221×31=31
在主持人选择B门开启后无汽车的情况下,参赛者选A门有汽车的概率 P ( A ∣ D ) = 1 3 P(A|D)=\frac{1}{3} P(A∣D)=31,因此后验概率并没有发生变化,并不是直观的 1 2 \frac{1}{2} 21,而仍然是 1 3 \frac{1}{3} 31。
因此,如果做调换门,那么相当于参赛者选择了C门,计算过程类似,概率为 2 3 \frac{2}{3} 32:
P ( C ∣ D ) = P ( D ∣ C ) P ( C ) P ( D ) P(C|D)=\frac{P(D|C)P(C)}{P(D)} P(C∣D)=P(D)P(D∣C)P(C)
P ( C ∣ D ) = 1 × 1 3 1 2 = 2 3 P(C|D)=\frac{1\times \frac{1}{3}}{\frac{1}{2}}=\frac{2}{3} P(C∣D)=211×31=32
3. 歧义的理解,扩展条件
3.1. 概述
蒙特霍尔问题之所以那么多年来争论不休,本质上是由于语义理解上的歧义;事实上,根据不同的理解方式,蒙特霍尔问题一共有 4 个本质不同的版本。如果不了解其他版本的话,那当你在现实中遇到其他蒙特霍尔问题的变体时,也会很容易想当然地给出错误的答案。
其实,这个问题一共有两个“歧义”点,缺一不可:
- 主持人是否能确保避免打开正确答案?
- 主持人是否一定会验证一个和你选择不同的门?
3.2. 歧义4个版本
根据这两个问题的答案,我们就得到了这个问题的 4 个版本:
- 版本1(标准版):主持人事先知道答案,会打开一扇你没选择的门,且其背后一定是羊;(1-是;2-是)
- 版本2(验证版):主持人事先并不知道答案,随机打开了一扇你没选择的门,其背后恰好是羊;(1-否;2-是)
- 版本3(机选版):主持人让系统随机打开一扇背后是羊的门,它恰好打开了一扇你没选择的门;(1-是;2-否)
- 版本4(随机版):主持人让系统随机打开一扇门,它恰好打开了一扇你没选择的门,且其背后是羊;(1-否;2-否)
注:1与2是指上面的歧义点。
那么,我们该怎么理解这 4 个版本的不同之处呢?它们的本质不同在于:主持人的行为是否需要承担泄露结果的「风险」,使得「条件概率」发生变动。易见,在最初的状态下,我们选中汽车的概率是 1/3。
- 版本1(标准版) ,无论我们是否选中汽车,主持人总能找到 1 个背后是羊的门,这件事情是 100% 能达成的,所以概率分布完全没变,我们选中汽车的概率依然为 1/3;
- 版本2(验证版),主持人显然冒了风险,如果你选中了羊,那他有 1/2 的概率会选中汽车,所以我们选中汽车的条件概率变成了 (1/3) /( 1/3+2/3×1/2)=1/2;
- 版本3(机选版),主持人其实也冒了风险,虽然不可能打开背后是汽车的门,但是在你选中羊的时候,有 1/2 的概率会随机你选择的门,所以我们选中汽车的条件概率变成了 (1/3) /(1/3+2/3×1/2)=1/2;
- 版本4(随机版),主持人显然冒了双重风险,一个风险是,打开了你选择的门;另一个风险是,它打开了你没选择的门,但其背后是汽车;在这种情况下,条件概率的分子分母都会变化;我们选中汽车的条件概率变成了(1/3×2/3)/(1/3×2/3+2/3×1/3)=1/2
除了「标准版」的答案是 1/3(应该换门)外,其他版本的答案均为 1/2 (换不换均可)。
由此可见,同一件事物对于不同人甚至掌握不同信息的同一个人概率可能不同。因此,概率并不能寄托在实际的物体上,而是存在于条件之下。
参考:
曾加. 蒙提霍尔问题(又称三门问题、山羊汽车问题)的正解是什么?. 知乎. 2022.04