📑前言

本文主要是【数据结构】——软件设计师——数据结构的文章，如果有什么需要改进的地方还请大佬指出⛺️

🎬作者简介：大家好，我是听风与他🥇
☁️博客首页：CSDN主页听风与他
🌄每日一句：狠狠沉淀，顶峰相见

1.下面有向图的拓扑序列是（ ）。

1.拓扑序列是有向无环图中所有顶点的一个线性序列，若有向图中存在弧<v，w>或存在从顶点v到w的路径，则在该有向图的任一拓扑序列中，v一定在w之前。下面有向图的拓扑序列是（ ）。

• (A) 41235
• (B) 43125
• © 42135
• (D) 41325

答案与解析

• 试题难度：容易
• 知识点：数据结构与算法基础>图的拓扑排序
• 试题答案：[[‘A’]]
• 试题解析：拓扑排序通俗一点来讲，其实就是依次遍历没有前驱结点的结点。而某一时刻没有前驱结点的结点有可能存在多个，所以一个图的拓扑排序可能有多个。
  4号结点没有前趋，所以拓扑排序的第一个元素是4。当4访问完了就可以访问1，1号访问完了就可以访问2，2号访问完了就可以访问3或5。所以拓扑排序结果为：41235。

2.若采用顺序存储结构，则平均需要移动（ ）个元素

2.设有一个包含n个元素的有序线性表。在等概率情况下删除其中的一个元素，若采用顺序存储结构，则平均需要移动（ ）个元素；若采用单链表存储，则平均需要移动（ ）个元素。

• (A) 1

• (B) (n-1)/2

• © logn

• (D) n

• (A) 0

• (B) 1

• © (n-1)/2

• (D) n/2

答案与解析

• 试题难度：一般

• 知识点：数据结构与算法基础>顺序表与链表

• 试题答案：[[B],[A]]

• 试题解析：

  若用顺序表存储，则最好情况是删除最后一个元素，此时不用移动任何元素，直接删除，最差的情况是删除第一个元素，此时需要移动n-1个元素，所以平均状态是移动(n-1)/2。

  若用链表存储，直接将需要删除元素的前趋next指针指向后继元素即可，不需要移动元素，所以移动元素个数为0。

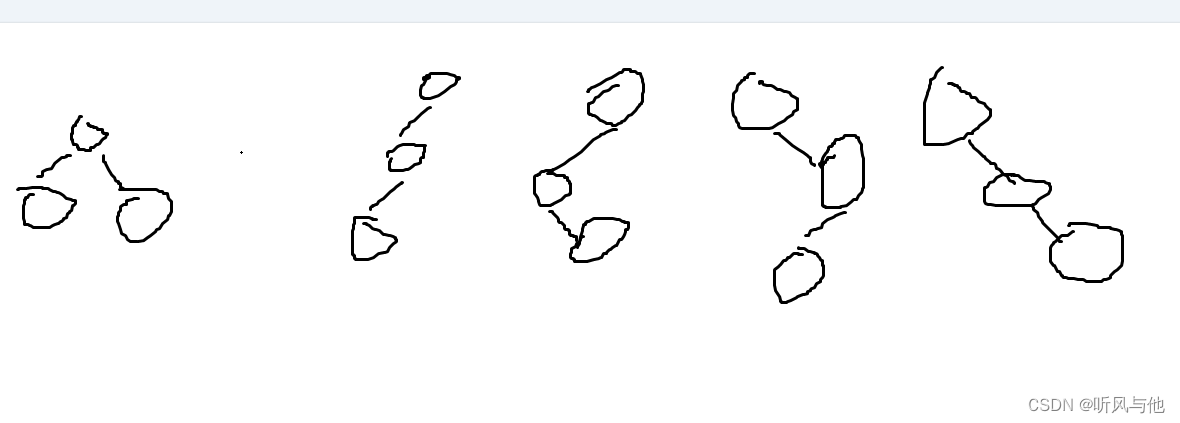
3.具有3个节点的二叉树有（ ）种形态。

• (A) 2
• (B) 3
• © 5
• (D) 7

答案：C

4.以下关于二叉排序树（或二叉查找树、二叉搜索树）的叙述

4.以下关于二叉排序树（或二叉查找树、二叉搜索树）的叙述中，正确的是（ ）。

• (A) 对二叉排序树进行先序、中序和后序遍历，都得到结点关键字的有序序列
• (B) 含有n个结点的二叉排序树高度为⌊log2n⌋+1
• © 从根到任意一个叶子结点的路径上，结点的关键字呈现有序排列的特点
• (D) 从左到右排列同层次的结点，其关键字呈现有序排列的特点

答案与解析

• 试题难度：一般
• 知识点：数据结构与算法基础>二叉排序树
• 试题答案：[[‘D’]]
• 试题解析：对于二叉排序树的遍历，只有中序遍历可以得到递增的有序序列，而后序遍历和先序遍历都不可以，因此A选项错误。
  对于二叉排序树的构造，最差可能会形成单枝树，因此节点数与树的高度，没有绝对的关系，B选项错误。
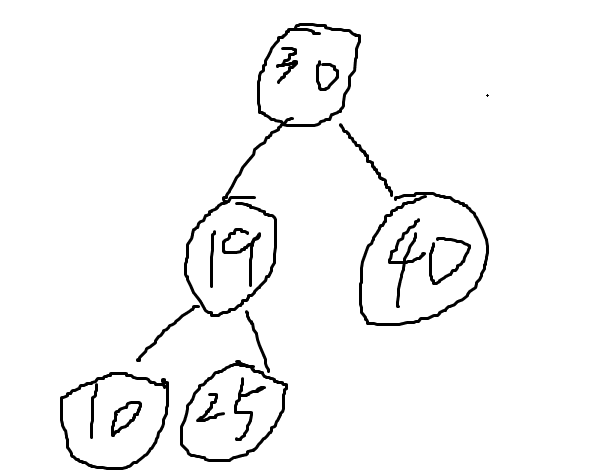
  对于二叉树的路径，只能保证当前节点与其子节点的大小关系，而对于下层节点，并不能保证与其他节点的大小。比如，对于根节点为30，其左孩子为19，右孩子为40；对于19的左孩子为10，右孩子为25；则从30→25，路径为30，19，25，并不是有序序列。因此C选项错误。
  对于D选项，对于二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
  （1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；
  （2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
  （3）左、右子树也分别为二叉排序树
  那么同层次的节点，右子树大于根节点，根节点大于左子树，则右子树大于左子树，则同层次有序排列。

5.令其所有元素依次通过一个初始为空的栈后

5.对于一个长度为n（n>1）且元素互异的序列，令其所有元素依次通过一个初始为空的栈后，再通过一个初始为空的队列。假设队列和栈的容量都足够大，且只要栈非空就可以进行出栈操作，只要队列非空就可以进行出队操作，那么以下叙述中，正确的是（ ）。

• (A) 出队序列和出栈序一定互为逆序
• (B) 出队序列和出栈序列一定相同
• © 入栈序列与入队序列一定相同
• (D) 入栈序列与入队序列一定互为逆序

答案与解析

• 试题难度：一般
• 知识点：数据结构与算法基础>队列与栈
• 试题答案：[[‘B’]]
• 试题解析：从题目的描述来看，出栈之后，直接入队，然后出队。所以：入队序列=出栈序列，又因为出队序列=入队序列。所以出队序列和出栈序列一定相同。

📑文章末尾