文章目录
- 一、强化学习问题
- 1、交互的对象
- 2、强化学习的基本要素
- 3、策略(Policy)
- 4、马尔可夫决策过程
- 5、强化学习的目标函数
- 1. 总回报(Return)
- 2. 折扣回报(Discounted Return)
- a. 折扣率
- b. 折扣回报的定义
- 3. 目标函数
- a. 目标函数的定义
- 2. 目标函数的解释
- 3. 优化目标
- 4、智能体走迷宫
- a. 问题
- b. 解析
一、强化学习问题
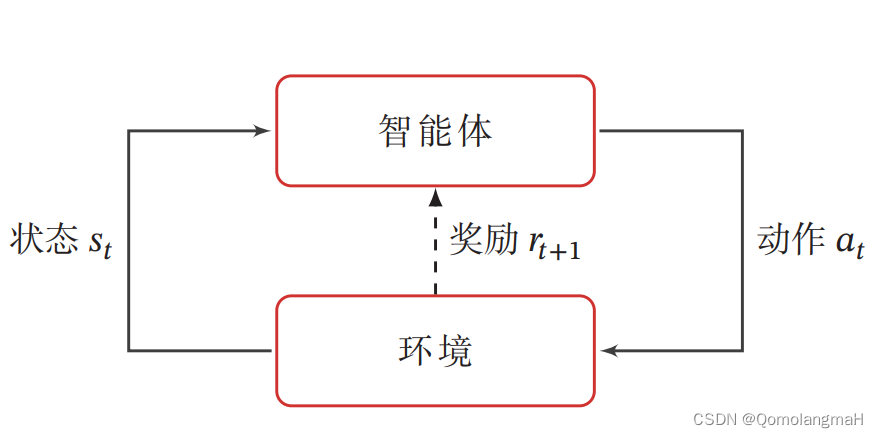
强化学习的基本任务是通过智能体与环境的交互学习一个策略,使得智能体能够在不同的状态下做出最优的动作,以最大化累积奖励。这种学习过程涉及到智能体根据当前状态选择动作,环境根据智能体的动作转移状态,并提供即时奖励的循环过程。
1、交互的对象
在强化学习中,有两个可以进行交互的对象:智能体和环境
-
智能体(Agent):能感知外部环境的状态(State)和获得的奖励(Reward),并做出决策(Action)。智能体的决策和学习功能使其能够根据状态选择不同的动作,学习通过获得的奖励来调整策略。
-
环境(Environment):是智能体外部的所有事物,对智能体的动作做出响应,改变状态,并反馈相应的奖励。
2、强化学习的基本要素
强化学习涉及到智能体与环境的交互,其基本要素包括状态、动作、策略、状态转移概率和即时奖励。
-
状态(State):对环境的描述,可能是离散或连续的。
-
动作(Action):智能体的行为,也可以是离散或连续的。
-
策略(Policy):智能体根据当前状态选择动作的概率分布。
-
状态转移概率(State Transition Probability):在给定状态和动作的情况下,环境转移到下一个状态的概率。
-
即时奖励(Immediate Reward):智能体在执行动作后,环境反馈的奖励。
3、策略(Policy)
策略(Policy)就是智能体如何根据环境状态 𝑠 来决定下一步的动作 𝑎(智能体在特定状态下选择动作的规则或分布)。
- 确定性策略(Deterministic Policy) 直接指定智能体应该采取的具体动作
- 随机性策略(Stochastic Policy) 则考虑了动作的概率分布,增加了对不同动作的探索。
上述概念可详细参照:【深度学习】强化学习(一)强化学习定义
4、马尔可夫决策过程
为了简化描述,将智能体与环境的交互看作离散的时间序列。智能体从感知到的初始环境 s 0 s_0 s0 开始,然后决定做一个相应的动作 a 0 a_0 a0,环境相应地发生改变到新的状态 s 1 s_1 s1,并反馈给智能体一个即时奖励 r 1 r_1 r1,然后智能体又根据状态 s 1 s_1 s1做一个动作 a 1 a_1 a1,环境相应改变为 s 2 s_2 s2,并反馈奖励 r 2 r_2 r2。这样的交互可以一直进行下去: s 0 , a 0 , s 1 , r 1 , a 1 , … , s t − 1 , r t − 1 , a t − 1 , s t , r t , … , s_0, a_0, s_1, r_1, a_1, \ldots, s_{t-1}, r_{t-1}, a_{t-1}, s_t, r_t, \ldots, s0,a0,s1,r1,a1,…,st−1,rt−1,at−1,st,rt,…,其中 r t = r ( s t − 1 , a t − 1 , s t ) r_t = r(s_{t-1}, a_{t-1}, s_t) rt=r(st−1,at−1,st) 是第 t t t 时刻的即时奖励。这个交互过程可以被视为一个马尔可夫决策过程(Markov Decision Process,MDP)。
关于马尔可夫决策过程可详细参照:【深度学习】强化学习(二)马尔可夫决策过程
5、强化学习的目标函数
强化学习的目标是通过学习到的策略 π θ ( a ∣ s ) \pi_{\theta}(a|s) πθ(a∣s) 来最大化期望回报(Expected Return),即希望智能体执行一系列动作以获取尽可能多的平均回报。
- 总回报:对于一次交互过程的轨迹,总回报是累积奖励的和。
- 折扣回报:引入折扣率,考虑未来奖励的权重。
1. 总回报(Return)
总回报(Total Return)指智能体与环境一次交互过程中所累积的奖励。给定一个策略 π ( a ∣ s ) \pi(a|s) π(a∣s),智能体与环境的交互过程可以通过轨迹 τ \tau τ 来表示,而这个轨迹的总回报 G ( τ ) G(\tau) G(τ) 可以通过累积奖励的方式进行计算。
-
总回报 G ( τ ) G(\tau) G(τ) 定义:
G ( τ ) = ∑ t = 0 T − 1 r t + 1 G(\tau) = \sum_{t=0}^{T-1} r_{t+1} G(τ)=t=0∑T−1rt+1其中 T T T 表示交互的总时长, r t + 1 r_{t+1} rt+1 表示在时刻 t + 1 t+1 t+1 获得的即时奖励。 -
总回报也可以通过奖励函数的形式表示:
G ( τ ) = ∑ t = 0 T − 1 r ( s t , a t , s t + 1 ) G(\tau) = \sum_{t=0}^{T-1} r(s_t, a_t, s_{t+1}) G(τ)=t=0∑T−1r(st,at,st+1)
这里, r ( s t , a t , s t + 1 ) r(s_t, a_t, s_{t+1}) r(st,at,st+1) 表示在状态 s t s_t st 下执行动作 a t a_t at 后转移到状态 s t + 1 s_{t+1} st+1 所获得的奖励。
2. 折扣回报(Discounted Return)
a. 折扣率
对于存在终止状态(Terminal State)的任务,当智能体到达终止状态时,交互过程结束,这一轮的交互称为一个回合(Episode)或试验(Trial)。一般强化学习任务都是回合式任务(Episodic Task),如下棋、玩游戏等。
然而,对于一些持续式任务(Continuing Task),其中不存在终止状态,智能体的交互可以无限进行下去,即 T = ∞ T = \infty T=∞。在这种情况下,总回报可能会无穷大。为了解决这个问题,引入了折扣率 γ \gamma γ。
b. 折扣回报的定义
-
折扣回报(Discounted Return)定义:
G ( τ ) = ∑ t = 0 T − 1 γ t r t + 1 G(\tau) = \sum_{t=0}^{T-1} \gamma^t r_{t+1} G(τ)=t=0∑T−1γtrt+1
其中 γ \gamma γ 是折扣率, γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ∈[0,1]。折扣率的引入可以看作是对未来奖励的一种降权,即智能体更加关注即时奖励和近期奖励,而对于远期奖励的关注逐渐减弱。- 当 γ \gamma γ 接近于 1 时,更加关注长期回报;
- 当 γ \gamma γ 接近于 0 时,更加关注短期回报。
-
折扣回报的定义在数学上确保了总回报的有限性,同时在实际应用中使得智能体更好地平衡长期和短期回报。
3. 目标函数
强化学习的目标是通过学习一个良好的策略来使智能体在与环境的交互中获得尽可能多的平均回报。
a. 目标函数的定义
强化学习的目标函数 J ( θ ) J(\theta) J(θ) 定义如下:
J ( θ ) = E τ ∼ p θ ( τ ) [ G ( τ ) ] = E τ ∼ p θ ( τ ) [ ∑ t = 0 T − 1 γ t r t + 1 ] J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[G(\tau)] = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t=0}^{T-1} \gamma^t r_{t+1}\right] J(θ)=Eτ∼pθ(τ)[G(τ)]=Eτ∼pθ(τ)[t=0∑T−1γtrt+1]其中, θ \theta θ 表示策略函数的参数, τ \tau τ 表示强化学习的轨迹。
- 这个目标函数表达的是在策略 π θ \pi_{\theta} πθ 下,智能体与环境交互得到的总回报的期望。(这个期望是对所有可能的轨迹进行的)
2. 目标函数的解释
- J ( θ ) J(\theta) J(θ) 可以看作是在策略 π θ \pi_{\theta} πθ 下执行动作序列的期望回报。
- 引入折扣率 γ \gamma γ 是为了在计算期望回报时对未来奖励进行折扣,使得智能体更加关注即时奖励和近期奖励。
- 目标函数 J ( θ ) J(\theta) J(θ) 的最大化等价于寻找最优的策略参数 θ \theta θ,使得智能体在与环境的交互中获得最大的长期回报。
3. 优化目标
强化学习的优化目标就是通过调整策略函数的参数 θ \theta θ,使得目标函数 J ( θ ) J(\theta) J(θ) 达到最大值。这个优化问题通常通过梯度上升等优化方法来解决,其中梯度由策略梯度定理给出。
4、智能体走迷宫
a. 问题
让一个智能体通过强化学习来学习走迷宫,如果智能体走出迷宫,奖励为 +1,其他状态奖励为 0.智能体的目标是最大化期望回报.当折扣率 𝛾 = 1 时,智能体是否能学会走迷宫的技巧?如何改进?
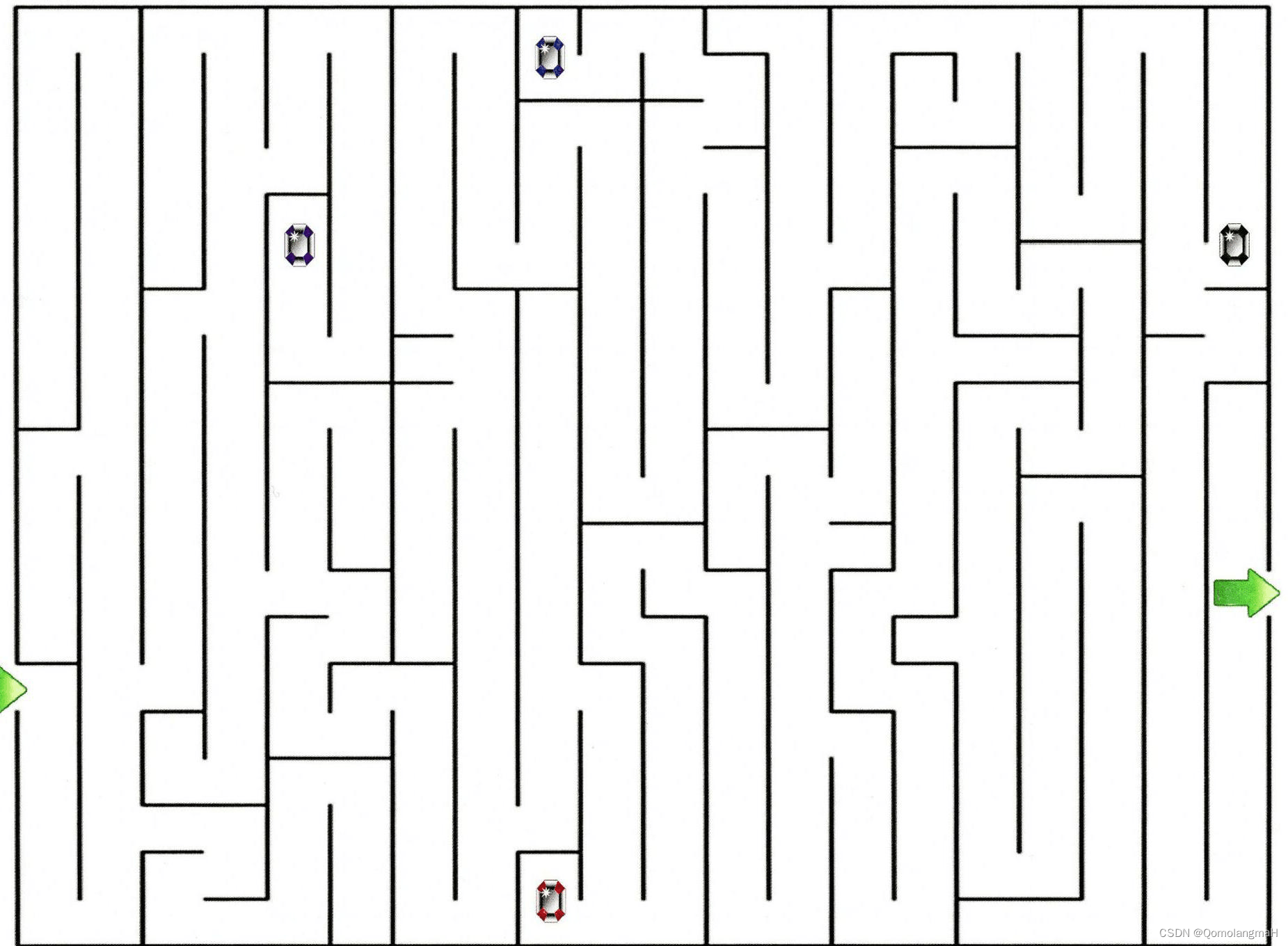
b. 解析
走迷宫任务存在终止状态(即走出迷宫),为回合式任务,智能体的交互不会无限地进行下去。由题意,当智能体出迷宫时有奖励+1,其他时刻奖励均为0。若折扣率为1,当该策略无法走出迷宫时,不会取得回报;当该策略可以走出迷宫,虽然达到了目标,但或许存在“绕远”的情况,即此时不一定为最优策略。
- 改进
- 尝试不同的折扣率:尝试使用较小的折扣率(0~1之间),以降低远期回报的权重,更强调即时奖励,加速学习过程。由目标函数可知,折扣率在0-1之间时,T越小则J越优,即智能体会学习到一个尽量快地走到终点的策略。
- 限制轨迹长度: 智能体会存在n个能够走出迷宫的轨迹(原地徘徊、来回绕路……),若考虑限制每个轨迹的长度,则可防止智能体无限地试验,更有可能学到直接走出迷宫的策略。
- 设置更复杂的奖励结构:尝试在迷宫中的每走一步都给予负奖励-1,在成功走出迷宫时给予大的正奖励100,以鼓励智能体更快地找到走出迷宫的策略。
- 使用深度强化学习:例如深度 Q 网络(DQN)或者深度确定性策略梯度(DDPG),这些方法通常可以更好地处理复杂的状态空间和动作空间,提高学习的效率。


![[蓝桥杯刷题]合并区间、最长不连续子序列、最长不重复数组长度](https://img-blog.csdnimg.cn/direct/5d41d6ee92e044b4a1d8a29fdf11973f.gif#pic_center)



![Enterprise Portal Standard Edition [WS_ENT_STD]](https://img-blog.csdnimg.cn/direct/3e17639a581e41af8ec8d01e37075425.png)