系列文章目录

---

前言

        我们介绍了 Crocoddyl（Contact RObot COntrol by Differential DYnamic Library），这是一个专为高效多触点优化控制（multi-contact optimal control）而定制的开源框架。Crocoddyl 可高效计算给定预定义接触序列（predefined sequence of contacts）的状态轨迹（state trajectory）和控制策略（control policy）。其效率得益于稀疏分析导数（sparse analytical derivatives）的使用、对问题结构的利用以及数据共享。它利用微分几何（differential geometry）来正确描述任何几何系统（如浮动基座系统（floating-base systems））的状态。

        此外，我们还提出了一种名为易损微分动态编程（Feasibility-prone Differential Dynamic Programming，FDDP）的新型多重打靶法（multiple-shooting method）。然而，我们的方法并没有增加额外的决策变量（decision variables），而额外的决策变量往往会因因式分解而增加每次迭代的计算时间。与经典的差分动态编程（DDP）算法相比，我们的新方法具有更强的全局化策略。具体来说，我们对经典 DDP 算法提出了两点修改。首先，后向传递接受不可行的状态控制轨迹。其次，在早期的 "探索性 "迭代中，滚动保持间隙开放（这是仅有相等约束的多重射击方法所期望的）。我们用不同的任务展示了我们框架的性能。利用我们的方法，我们可以在几毫秒的时间内计算出腿式机器人的高动态机动性（highly-dynamic maneuvers）（如跳跃（jumping）、前空翻（front-flip））。

        Crocoddyl 是一个用于接触序列下机器人控制的最优控制库。它的求解器基于新颖高效的微分动态编程（DDP）算法。Crocoddyl 可计算最佳轨迹和反馈增益。它使用 Pinocchio 快速计算机器人动力学和分析导数。

        如果您想了解有关 Crocoddyl 及其求解器的更多信息，我们建议您阅读 [1] [2] [3] 并访问 PUBLICATIONS.md。如果您想了解当前的发展情况并做出贡献，请直接访问开发分支。

---

一、特点

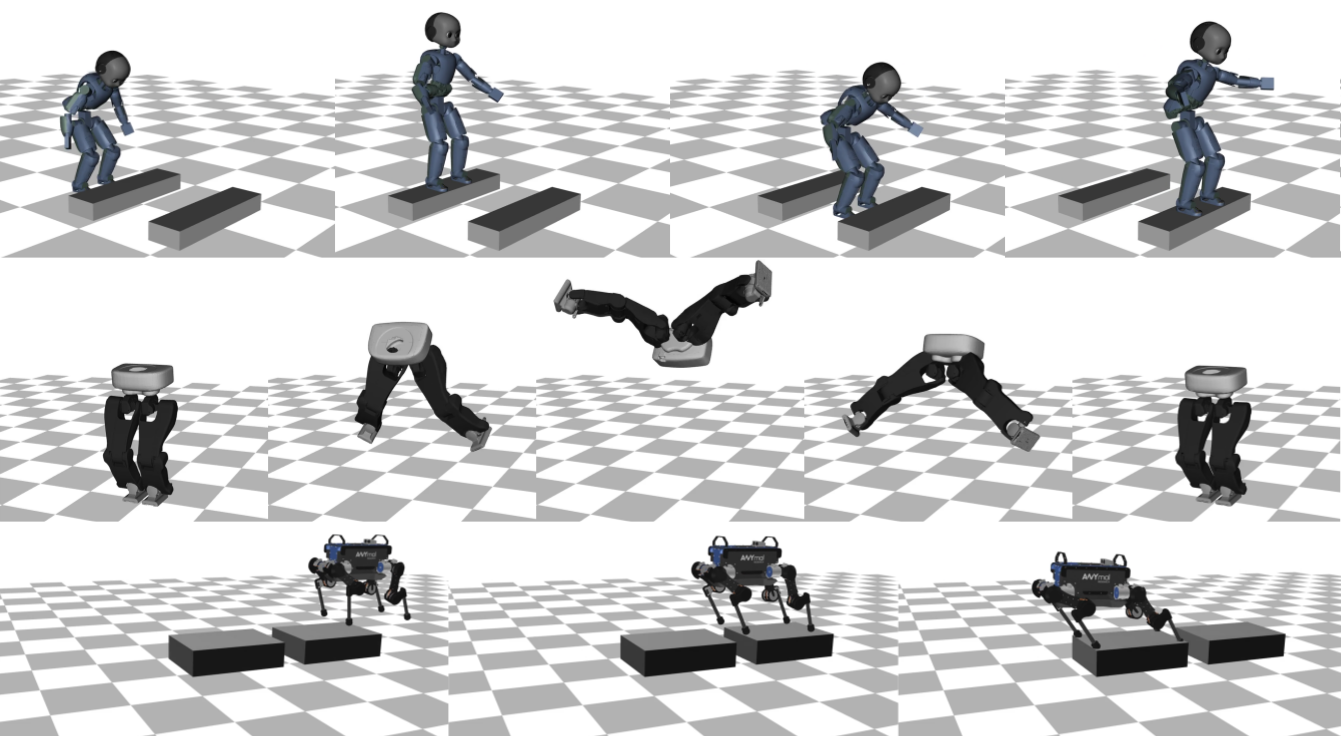
        Crocoddyl 功能多样：

• 各种最优控制求解器（DDP、FDDP、BoxFDDP、Ipopt 等）
• 通过 Pinocchio 实现分析和稀疏导数
• 利用 Pinocchio 支持微分几何
• 各种积分器、动力学、成本和约束条件
• 数值微分支持
• 通过 CppAD 支持自动微分

        Crocoddyl 高效灵活：

• 高速缓存友好
• 通过 OpenMP 支持多线程
• 通过 Boost Python 绑定 Python（包括抽象
• 兼容 C++14/17/20
• 经过广泛测试
• 通过 CppADCodeGen 支持自动代码生成

 

 

二、安装

        Crocoddyl 可以轻松安装在各种 Linux（Ubuntu、Fedora 等）和 Unix 发行版（Mac OS X、BSD 等）上。以下是安装 Crocoddyl 的不同方法。

2.1 Conda

   conda install crocoddyl -c conda-forge

2.2 pypi

  pip install --user crocoddyl

 2.3 ROS

        只需将其克隆（使用 --recursive 命令）到 catkin 工作区并编译即可。

2.3.1 📦 从 Debian / Ubuntu 软件包中使用 robotpkg

        如果您从未添加过 robotpkg 的软件仓库，现在就添加吧：

sudo tee /etc/apt/sources.list.d/robotpkg.list <<EOF
deb [arch=amd64] http://robotpkg.openrobots.org/packages/debian/pub $(lsb_release -sc) robotpkg
EOFcurl http://robotpkg.openrobots.org/packages/debian/robotpkg.key | sudo apt-key add -
sudo apt update

         安装 Crocoddyl 及其 Python 绑定：

sudo apt install robotpkg-py3\*-crocoddyl

        配置环境变量 

export PATH=/opt/openrobots/bin:$PATH
export PKG_CONFIG_PATH=/opt/openrobots/lib/pkgconfig:$PKG_CONFIG_PATH
export LD_LIBRARY_PATH=/opt/openrobots/lib:$LD_LIBRARY_PATH
export PYTHONPATH=/opt/openrobots/lib/python3.10/site-packages:$PYTHONPATH

三、文档

        这里有 Crocoddyl 的 Doxygen 文档。或者，你也可以查看 Jupyter 笔记本。按以下顺序开始

examples/notebooks/unicycle_towards_origin.ipynb
examples/notebooks/cartpole_swing_up.ipynb
examples/notebooks/arm_manipulation.ipynb
examples/notebooks/whole_body_manipulation.ipynb
示例/笔记本/双足行走.ipynb
examples/notebooks/introduction_too_crocoddyl.ipynb
        此外，安装完成后，您可以按如下方式运行示例：

python -m crocoddyl.examples.quadrupedal_gaits "display" "plot" # enable display and plot

        或运行构建目录中的示例、单元测试和基准测试，如

cd build
make test
make -s examples-quadrupedal_gaits INPUT="display plot" # enable display and plot
make -s benchmarks-cpp-quadrupedal_gaits INPUT="100 walk" # number of trials ; type of gait

         在这里可以使用环境变量来显示和/或绘制由我们的示例生成的图表：

export CROCODDYL_DISPLAY=1
export CROCODDYL_PLOT=1

四、引用 Crocoddyl

        在学术研究中引用 Crocoddyl 时，请使用以下 BibTeX 行：

@inproceedings{mastalli20crocoddyl,author={Mastalli, Carlos and Budhiraja, Rohan and Merkt, Wolfgang and Saurel, Guilhem and Hammoud, Bilaland Naveau, Maximilien and Carpentier, Justin and Righetti, Ludovic and Vijayakumar, Sethu and Mansard, Nicolas},title={{Crocoddyl: An Efficient and Versatile Framework for Multi-Contact Optimal Control}},booktitle = {IEEE International Conference on Robotics and Automation (ICRA)},year={2020}
}

        请考虑引用 PUBLICATIONS.md 中描述的我们的部分出版物和贡献。

        Crocoddyl 的贡献不仅限于高效的软件开发。也请考虑引用我们不同求解器和公式的算法贡献：

• 可行性驱动 DDP (FDDP)： [1]
• 控制受限的可行性驱动 DDP（Box-FDDP）： [2]
• 反动力学轨迹优化和相等约束 DDP 求解器（Intro 求解器）： [3]

        最后，还请考虑引用 Pinocchio，它为刚体算法及其导数的高效实施做出了贡献。有关如何引用 Pinocchio 的更多详情，请访问：https://github.com/stack-of-tasks/pinocchio。

五、部分出版物

[1] C. Mastalli, R. Budhiraja, W. Merkt, G. Saurel, B. Hammoud, M. Naveau, J. Carpentier, L. Righetti, S. Vijayakumar and N. Mansard. Crocoddyl: An Efficient and Versatile Framework for Multi-Contact Optimal Control, IEEE International Conference on Robotics and Automation (ICRA), 2020

[2] C. Mastalli, W. Merkt, J. Marti-Saumell, H. Ferrolho, J. Sola, N. Mansard and S. Vijayakumar. A Feasibility-Driven Approach to Control-Limited DDP, Autonomous Robots, 2022

[3] C. Mastalli, S. P. Chhatoi, T. Corbères, S. Tonneau and S. Vijayakumar. Inverse-Dynamics MPC via Nullspace Resolution, IEEE Transactions on Robotics, 2023