测试函数为F9
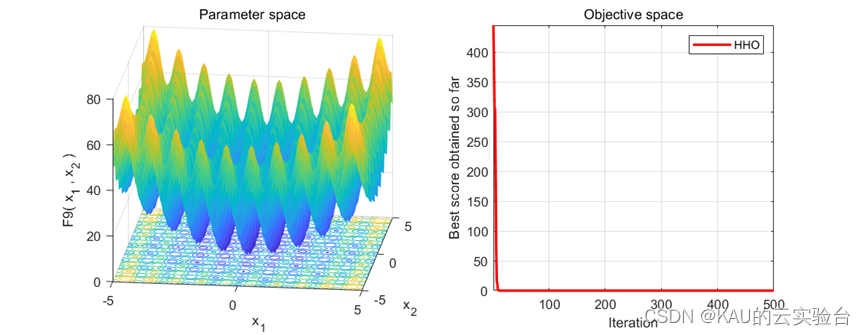
在MATLAB中执行程序结果如下:
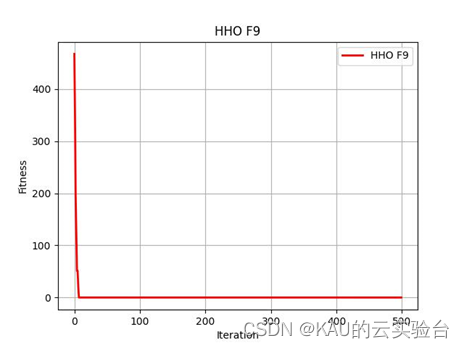
在Python中执行程序结果如下:
哈里斯鹰优化算法(Harris Hawks Optimization , HHO)是 Heidari等[1]于2019年提出的一种新型元启发式算法,设计灵感来源于哈里斯鹰在捕食猎物过程中的合作行为以及突然袭击的狩猎风格,算法的寻优过程包括探索、探索与开发转换和开发三个阶段。具有需调参数少、原理简单易实现、局部搜索能力强等优点。在数值和工程优化、图像识别、故障诊断、电网优化设计、等工程领域得到广泛的应用。
本文作者将详细介绍其原理、代码实现,并分析可以进行改进的方向。
00 目录
1 哈里斯鹰优化算法(HHO)原理
2 代码目录
3 算法性能
4 算法的改进与利用
5 源码获取
01 哈里斯鹰优化算法(HHO)原理
HHO算法通过模仿哈里斯鹰在捕食猎物过程中的合作行为以及突然袭击的狩猎风格。HHO算法共有三个阶段,全局探索阶段、全局探索向局部开发转换阶段和局部开发阶段。在HHO 算法中,哈里斯鹰的位置被当作为候选解,迭代的最佳候选解为猎物。
1.1 探索阶段
探索阶段,哈里斯鹰种群个体随机栖息在各地,根据其敏锐的眼睛在沙漠空间中跟踪和探测猎物,通过两种策略对猎物进行等概率的全局搜索,P<0.5时,每只鹰会根据其他成员和猎物位置进行移动,P>=0.5时,哈里斯鹰会随机栖息在种群范围内的某棵树上,其表达式如下:
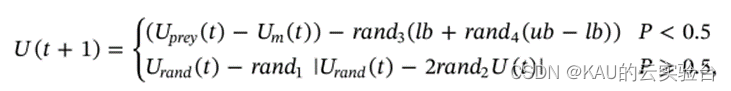
其中, Urand为第t代种群中随机选择的哈里斯鹰个体;Uprey表示猎物位置;Um表示当前哈里斯鹰种群的平均位置;ub, lb分别为搜索范围上限和下限;rand1234和P均为(0,1)区间内的随机数。
1.2 探索与开发转换阶段
HHO算法根据哈里斯鹰捕猎习性将其捕猎过程划分为探索行为和开发行为,猎物在逃跑过程中能量会逐渐降低,因此采用猎物逃逸能量动态选取探索行为或开发行为进行捕猎,猎物逃逸能量定义为:
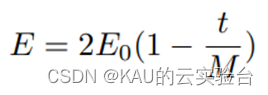
其中,E0为猎物的初始逃逸能量,是在(-1,1)之间的随机数,t为当前进化代数,M为种群最大进化代数。当|E|>=1时进入探索阶段,|E|<1时进入开发阶段。
1.3 开发阶段
在找到目标猎物后,哈里斯鹰在开发阶段发起攻击,其会在猎物周围形成一圈围攻,等待突然袭击的机会。然而,实际的捕食过程是复杂的,例如,被围困的猎物可能会逃脱包围圈,哈里斯鹰可以根据猎物的行为作出必要的调整。因此,HHO采用四种策略来模仿哈里斯鹰的狩猎行为,这四种策略分别是软包围、硬包围、渐进式快速俯冲的软包围和渐进式快速俯冲的硬包围。
定义Sp为猎物逃逸概率,其为(0,1)之间的随机数,Sp<0.5表示有逃脱机会,结合猎物逃逸能量|E|和猎物逃逸概率Sp确定狩猎策略。
a. 当0.5 ≤ |E| < 1且Sp ≥ 0.5时-软包围
猎物仍然有逃逸的能量,试图通过随机的跳跃逃出包围圈,此时,鹰使用软包围捕食猎物以使其精疲力尽,从而使鹰可以突击突袭,其更新公式为:
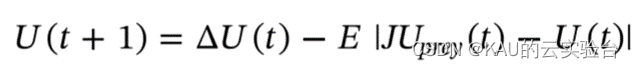
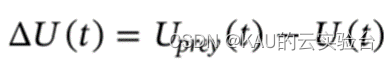
其中,ΔU为猎物位置和当前个体位置之差,J~U(0,2)。
b. 当|E| < 0.5且Sp ≥ 0.5时-硬包围
猎物没有逃逸的能量,也没有逃脱的机会,哈里斯鹰使用硬包围捕食猎物以进行最后突击突袭,其更新公式为:
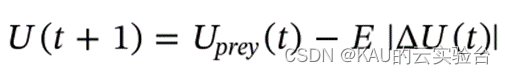
c. 当0.5 ≤ |E| < 1且Sp < 0.5时-渐进式快速俯冲软包围
猎物有机会从包围圈中逃脱,且有足够能量逃脱鹰的捕捉,但是哈里斯鹰会围绕猎物采用渐进式快速俯冲软包围,并根据猎物的欺骗性行为逐渐纠正其位置和方向,从而选择最佳位置来捕捉猎物,通过以下两个策略实施。当第一个策略无效时,执行第二个策略,其更新公式为:
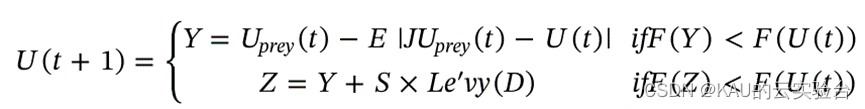
其中,F(.)是适应度函数;S是元素为(0,1)之间d维随机向量;Levy为莱维飞行策略,其公式为:

d. 当|E| < 0.5且Sp < 0.5时-渐进式快速俯冲硬包围
猎物筋疲力尽,但仍有机会逃脱,哈里斯鹰通过渐进式快速俯冲硬包围猎物,此策略鹰的更新位置公式与渐进式快速俯冲的软包围中的公式相似。在这种情况下,哈里斯鹰群试图缩短它们与目标猎物的平均位置的距离,其更新公式为:
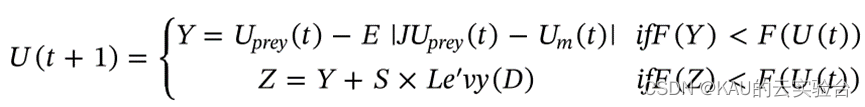
算法流程如下:
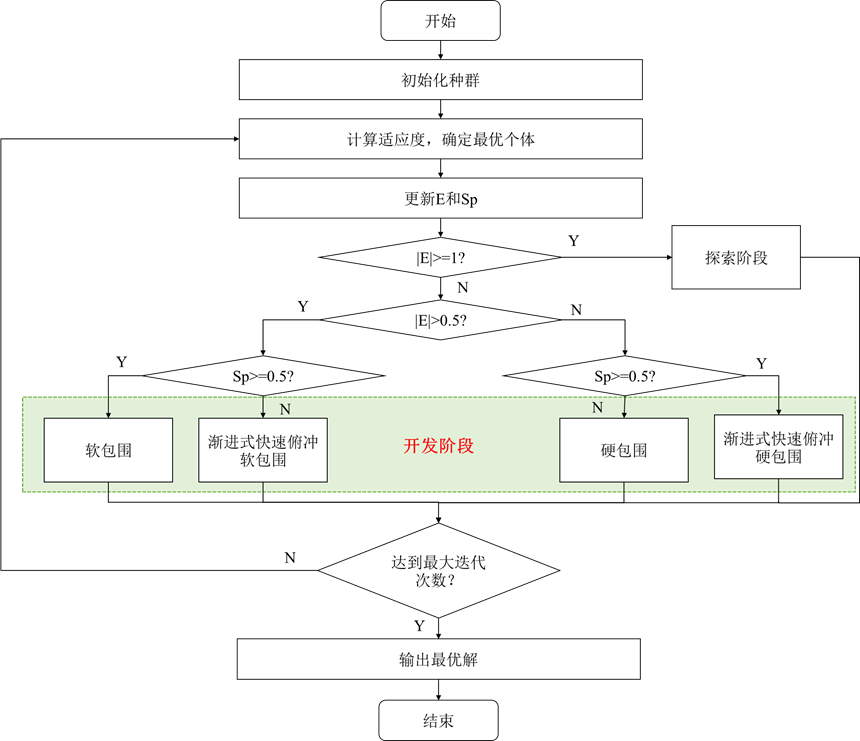
02 代码目录

代码包含MATLAB和Python,考虑到很多同学获取代码后,MATLAB代码部分有乱码(MATLAB版本问题),可以将MATLAB版本改为2020及以上,或使用乱码解决文件夹中的txt文件即可。
代码都经过作者重新注释编写,代码更清爽,可读性强。
部分代码:
MATLAB:

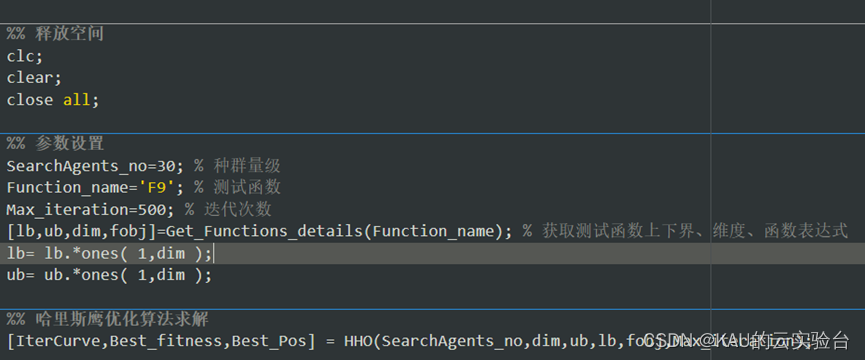
Python:
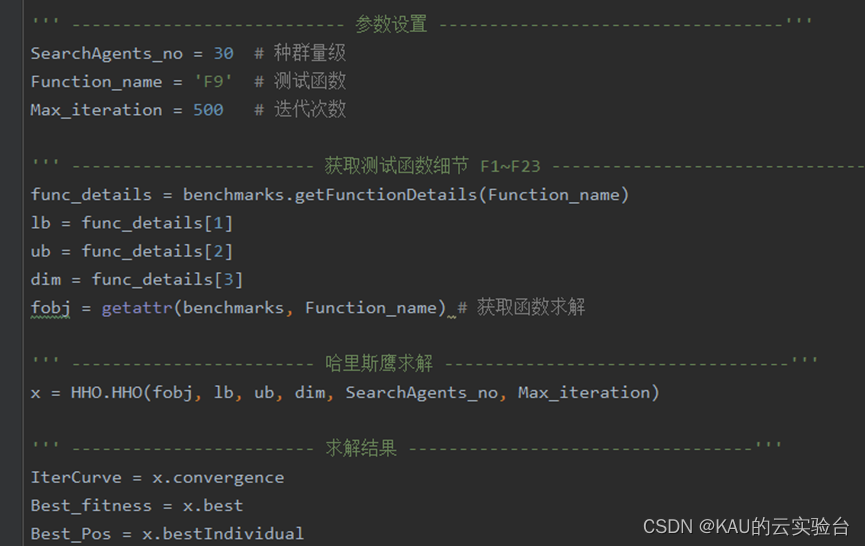
03 算法性能
采用标准测试函数初步检验其寻优性能
在MATLAB中执行程序结果如下:
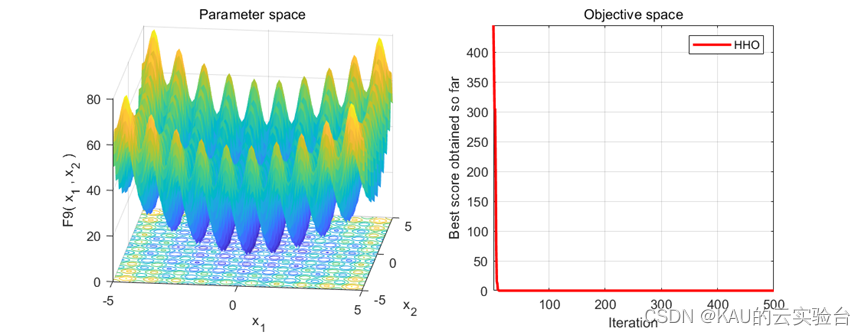
Python中执行程序结果如下:
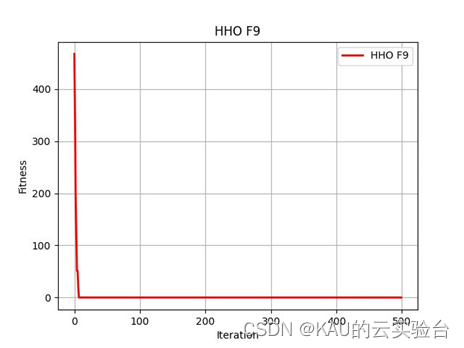
MATLAB和Python都进行了F9函数的测试,测试效果都不错,其收敛速度和精度很好。
04 算法的改进与利用
根据没有免费的午餐(NFL)定理[2],没有一个算法可以处理所有的优化问题,即每个算法都有其优势和局限性,这也激励着学者提出各种改进的算法来解决不同类型的优化问题,同时也为算法间的混合利用提供了参考。这一节作者就简要谈一下HHO的可改进之处及其可利用的优点。
4.1 改进
HHO算法通过4种策略进行局部开发,在开发阶段具有良好的表现,但其探索阶段对于更复杂的优化问题效率并不高,可能会过早收敛,因此可以对其探索阶段的更新方式进行改进,避免在探索阶段种群陷入局部最优。
其次,HHO依赖于一个线性递减方法来改变逃逸能量因子,这会导致勘探和开发不平衡,且无法准确表征实际情况下鹰与猎物多轮围捕逃逸过程,因为在迭代后期|E|必然小于1,只进行局部搜索,因此其搜索并不呈现全局性,若在前期种群接近局部最优,则可能导致后期算法陷入局部最优而无法跳出。可以通过一种非线性递减的方法来动态调整算法参数E。
4.2 利用
由HHO的理论可知,其在开发阶段采用了4种策略来围捕猎物,这样的策略能够使算法具有良好的局部搜索性能,可以作为其他算法提高局部搜索能力的方法之一。
05 源码获取
在GZH (KAU的云实验台) 后台回复 HHO
参考文献
[1] Heidari A A, Mirjalili S, Faris H, et al. Harris Hawks Optimization Algorithm and Applications[J]. Future Generation Computer Systems,2019,97(8):849-872.
[2] Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE transactions on evolutionary computation 67–82, 1997.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行),你们的鼓励就是我坚持的动力!