1. 问题描述
给定两个长度分别是m和n的数组,数组的每个元素都是数字0~9,从这两个数组当中选出k个数字来创建一个最大数,其中k满足k<=m+n,选出来的数字在创建最大数里的位置必须与在原数组内的相对位置一致。返回k个元素的整数数组,尽可能优化算法的时间复杂度和空间复杂度。
2. 问题示例
给出nums1=[3,4,6,5],nums2=[9,1,2,5,8,3],k=5,返回[9,8,6,5,3];给出nums1=[6,7],nums2=[6,0,4],k=5,返回[6,7,6,0,4];给出nums1=[3,9],nums2=[8,9],k=3,返回[9,8,9]。
3. 代码实现
使用贪心算法来解决。具体来说,我们可以固定从nums1中选取多少个数字,然后从nums2中选取剩余的数字,使得它们合起来构成一个长度为k的最大数。
为了实现这个算法,我们需要确定以下步骤:
- 实现一个函数,将一个数组中的元素重排,使得它们构成的数字最大;
- 对于一个给定的数组nums和整数k,我们需要找到由nums中的数字组成的长度为k的最大数;
- 给定两个数组nums1和nums2以及整数k,我们需要找到由nums1和nums2中的数字组成的长度为k的最大数。
def maxNumber(nums1, nums2, k):# 重排数组中的元素,使得它们构成的数字最大def merge(A, B):return [max(A, B).pop(0) for _ in A+B]# 找到由nums中的数字组成的长度为k的最大数def prepare(nums, k):drop = len(nums) - kout = []for num in nums:while drop and out and out[-1] < num:out.pop()drop -= 1out.append(num)return out[:k]# 找到由nums1和nums2中的数字组成的长度为k的最大数def lexicographically_greater(a, i, b, j):while i < len(a) and j < len(b) and a[i] == b[j]:i += 1j += 1return j == len(b) or (i < len(a) and a[i] > b[j])# 尝试从nums1中选取i个数字,从nums2中选取k-i个数字res = []for i in range(max(0, k-len(nums2)), min(k, len(nums1))+1):candidate = merge(prepare(nums1, i), prepare(nums2, k-i))res = max(candidate, res) if res != [] else candidatereturn res
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
result = maxNumber(nums1, nums2, k)
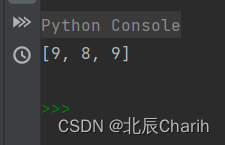
print(result) # 输出 [9, 8, 6, 5, 3]其中,函数merge()用于将两个数组合并成一个最大数,函数prepare()用于找到由一个数组中的数字组成的长度为k的最大数,函数lexicographically_greater()用于比较两个数组的字典序大小。具体来说,这个函数的作用是,给定两个数组a和b以及它们的起始下标i和j,如果在i和j之后,a比b字典序更大,则返回True,否则返回False。
在主函数maxNumber()中,我们枚举从nums1中选取的数字的个数i,然后从nums2中选取剩余的数字k-i,将它们合并成一个最大数candidate。最后,我们将所有生成的最大数中的最大者返回即可。这个算法的时间复杂度为O((m+n)^3),空间复杂度为O(m+n)。

采用动态规划的方法。具体来说,我们可以使用两个动态规划数组来保存最大数的信息,以减少重复计算。
def maxNumber(nums1, nums2, k):def get_max_subsequence(nums, k):stack = []pop_count = len(nums) - kfor num in nums:while pop_count and stack and stack[-1] < num:stack.pop()pop_count -= 1stack.append(num)return stack[:k]def merge(nums1, nums2):merged = []i, j = 0, 0while i < len(nums1) and j < len(nums2):if nums1[i:] > nums2[j:]:merged.append(nums1[i])i += 1else:merged.append(nums2[j])j += 1merged.extend(nums1[i:])merged.extend(nums2[j:])return mergedresult = []for i in range(max(0, k-len(nums2)), min(k, len(nums1))+1):subsequence1 = get_max_subsequence(nums1, i)subsequence2 = get_max_subsequence(nums2, k-i)merged = merge(subsequence1, subsequence2)result = max(result, merged)return result
nums1 = [6,7]
nums2 = [6,0,4]
k = 5
result = maxNumber(nums1, nums2, k)
print(result)在这个实现中,我们定义了两个辅助函数:get_max_subsequence()和merge()。函数get_max_subsequence()用于从一个数组中获取长度为k的最大子序列,这个函数的实现与之前贪心算法中的prepare()函数相同。函数merge()用于合并两个子序列,这个函数的实现与之前贪心算法中的merge()函数相同。
在主函数maxNumber()中,我们使用动态规划来生成最大数。我们首先枚举从nums1中选取的数字的个数i,然后使用get_max_subsequence()函数分别从nums1和nums2中获取长度为i和k-i的最大子序列。接下来,我们使用merge()函数将这两个子序列合并成一个最大数,并将其与之前的结果比较,保留更大的那个。最后,返回最终的最大数。这个算法的时间复杂度为O((m+n)^2),空间复杂度为O(m+n)。
使用单调栈的思想来减少重复计算。具体来说,我们可以使用两个单调递减栈,分别从nums1和nums2中构建。栈的长度为k,每次入栈时,判断当前元素与栈顶元素的大小关系,如果当前元素更大,则将栈顶元素出栈,直到满足栈的长度要求或者栈为空。然后将当前元素入栈。
def maxNumber(nums1, nums2, k):def build_max_stack(nums, k):stack = []drop_count = len(nums) - kfor num in nums:while drop_count > 0 and stack and stack[-1] < num:stack.pop()drop_count -= 1stack.append(num)return stack[:k]def merge(nums1, nums2):merged = []i, j = 0, 0while i < len(nums1) and j < len(nums2):if nums1[i:] > nums2[j:]:merged.append(nums1[i])i += 1else:merged.append(nums2[j])j += 1merged.extend(nums1[i:])merged.extend(nums2[j:])return mergedresult = []for i in range(max(0, k - len(nums2)), min(k, len(nums1)) + 1):subsequence1 = build_max_stack(nums1, i)subsequence2 = build_max_stack(nums2, k - i)merged = merge(subsequence1, subsequence2)result = max(result, merged)return result
nums1 = [3,9]
nums2 = [8,9]
k = 3
result = maxNumber(nums1, nums2, k)
print(result)在这个实现中,我们使用了两个辅助函数:build_max_stack()和merge()。函数build_max_stack()用于构建单调递减栈,获取长度为k的最大子序列。函数merge()用于合并两个子序列。
在主函数maxNumber()中,我们通过枚举从nums1中选取的数字的个数i,分别构建nums1和nums2的单调递减栈,并通过merge()函数将这两个子序列合并成一个最大数。最后,返回最终的最大数。这个算法的时间复杂度为O(m+n+k(m+n)),其中m和n分别是nums1和nums2的长度。