我吹捧 bbr 时曾论证过它在和 buffer 拧巴的时候表现如何优秀,但这一次说 vegas 时,我说的是从拥塞控制这个问题本身看来,vegas 为什么好,并且正确。
接着昨天 tcp vegas 鉴赏 继续扯。
假设一群共享带宽的流量中有流量退出或有新流量进入,剩余流如何感知到这事。loss-based 算法按照自己的步调填充 buffer 直到丢包,它们无法感知任何资源变化,而 bbr 则通过定期的 probe 来探测,但如果在 probe 之前有其它 bbr 流先行 probe,则后 probe 的流什么都拿不到。虽然它们都没有能力自动感知到资源变化,但它们无疑都希望自己能做到这一点。
本质上,大家都被灌输了 capacity-search 思想,想方设法要榨干最后 1k 的带宽,却往往适得其反,包括 bbr 在内的绝大多数算法引入越搞越复杂的 probe 机制,却没有收到应有的收益,而 vegas 采用松弛策略,反而自动做到了带宽利用率的最优化。
vegas 依靠 alpha < diff = (expected - actual) * basertt < beta 自动做到这一点。
如果有流量退出,所有流都会感知到 rtt 变小,actual 变大,diff 往左偏置,只要偏过左值 alpha,vegas 就会增加 cwnd 以适应这一变化。也就是说,流量退出腾出的 buffer 由大家公平瓜分了。
如果有流量进入,所有流都会感知到 rtt 变大,actual 变小,diff 往右偏置,只要偏过右值 beta,vegas 就会减少 cwnd 以适应这一变化,每条流都会腾出一些 inflight 分享给新进入的流。
vegas 是真正的拥塞控制。vegas 不做 capacity-search,我们看到,即使有流退出,也不会有单独的流抢走大多数带宽,因为 rtt 变化信号是大家同时可捕捉同时可反应的(相比之下,loss 信号则依赖比如说 red 丢谁没丢谁)。
再看 rtt 公平性。
diff = cwnd (1 - basertt / lastrtt) = cwnd (1 - basertt / (basertt + queuing_delay)) = cwnd (1 - 1 / (1 + queuing_delay / basertt)) ,设 basertt 是 y,cwnd 为 x,queuing_delay 为常数 q,diff = x(1 - 1 / (1 + q / y)) 要想把 diff 限制在相同的 alpha,beta 区间内,大家的 q 都是同一个,y 越大,x 越大,但带宽却一致,vegas 完美自适应 rtt。
不光如此,rtt 越小,带宽感知越灵敏,因为 rtt 越大,抖动代价越大,所谓尾大不掉,这不光影响自己,还影响其它流的公平性,因此 rtt 越大越趋向稳定。rtt 越大,获得的份额越小。其实 vegas 是按 bdp 分配带宽的,rtt 越大,buffer 占比越小,这是公平的根源。下面是简单的论证。
依旧设 basertt 是 y,cwnd 为 x,由于有流退出 q 由 2 减少到 1,diff 的 diff 为 q 变化前后两个 diff 相减,可表示为 z = -x / ((y + 2)(y + 1)),直观画图如下(就不求偏导了):
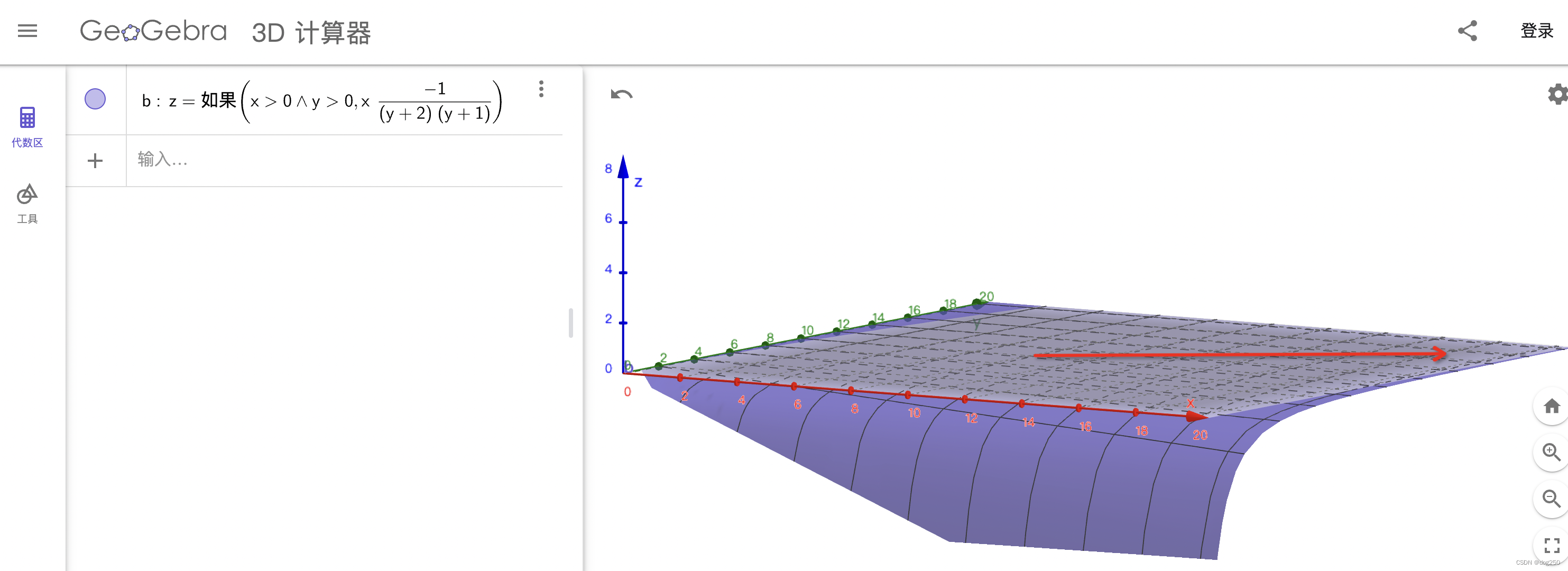
我们已经知道,y 越大,x 相对越大,如图所示(如果短肥管道,箭头贴着 x 轴,沿 y 轴存在 rtt 不公平,本文暂不谈),z 趋向于箭头指向的方向,在那里,平面非常平缓,这意味着,diff 受 basertt 影响非常小,对变化的感知力一致,进而能获得瓜分同样份额的 buffer,这就是公平的根源。
下面又是个有趣的重头戏。
vegas 对 loss 完全无感,因此它不得不修改 tcp 重传算法以适配它自己 “夹逼 diff 区间” 的算法。reno 早已深入人心,并且基于 loss-based reno 对拥塞控制做了标准化,有趣的是,包括 reno 在内的所有 loss-based cc 几乎都在使用 aimd 进行控制,而它们控制的并不是拥塞,vegas 专门控制拥塞的算法因为是后来的,反倒让人觉得奇怪。
vegas 不再使用 3 个dupack 触发重传,而采用了一种时间序方法,我这里截一个 vegas 原始论文 的图:

仔细看,这不就是 rack 嘛,关于 rack 可参考 rack 与 fack。rack 时间序最早正是来源于 vegas,它实际上在 rack 发布之前就早已被很多家公司运用。
时间序的一个重要作用就是解耦了重传和丢包检测。曾经重传依赖于某种丢包信号,比如 3 次 dupack 本身就算一种奇技淫巧,一旦等不到 3 次 dupack,这个机制就完全失效,其意义非常有限,但时间序重传不再依赖对端反馈,可源源不断提供可供传输的报文,剩下的交给拥塞控制。
有了时间序重传机制,就可以将丢包检测和重传分离,vegas 可完全不在乎 loss 而完全通过夹逼 diff 到 alpha,beta 区间完成拥塞控制,完全不再区分参与 diff 计算的是新数据还是重传数据,简洁而唯美。
linux tcp 内置了拥塞状态机,如今已经合入了 rack 作为除 dupack 之外的另一种触发重传的选择,并且已经支持 cong_control 回调完全接管整个拥塞控制而绕开拥塞状态机(比如 prr 会被绕开,因为如果不将 loss 做信号,也就没必要对 loss 反应那么大),我觉得可以实现一版完备的真 vegas 了,言外之意,此前的 vegas 是假的。
最后,vegas 改进了慢启动,不再盲目乘以 2,而是在慢启动期间加入了 diff 判断,从而择机退出慢启动 or 改变激进程度。
总之,从头看到尾,vegas 只有 diff 判断,任何时候(无论慢启动,重传等)只要算 diff 并和 alpha,beta 比较就行了,在这么简单的逻辑下,前面也简单论证过,vegas 的公平性和效率都非常好。
我曾经写过一个 cugas = cubic + vegas,但其实还不如将它变成 bbr 呢,如果世界上只有一种 vegas 就会非常稳定,因为天生公平的算法就不会引入很多公平性和效率之间的权衡问题,进而也不会引入号称能解决这些问题,结果只是新晋一员卷客,看看现在的拥塞控制领域那些不雅又奇怪的算法。
浙江温州皮鞋湿,下雨进水不会胖。