数据结构和算法笔记2：二分法

二分法网上有两种写法，一种左闭右闭，一种左闭右开，个人习惯左闭右闭的写法，

有序数组查找数

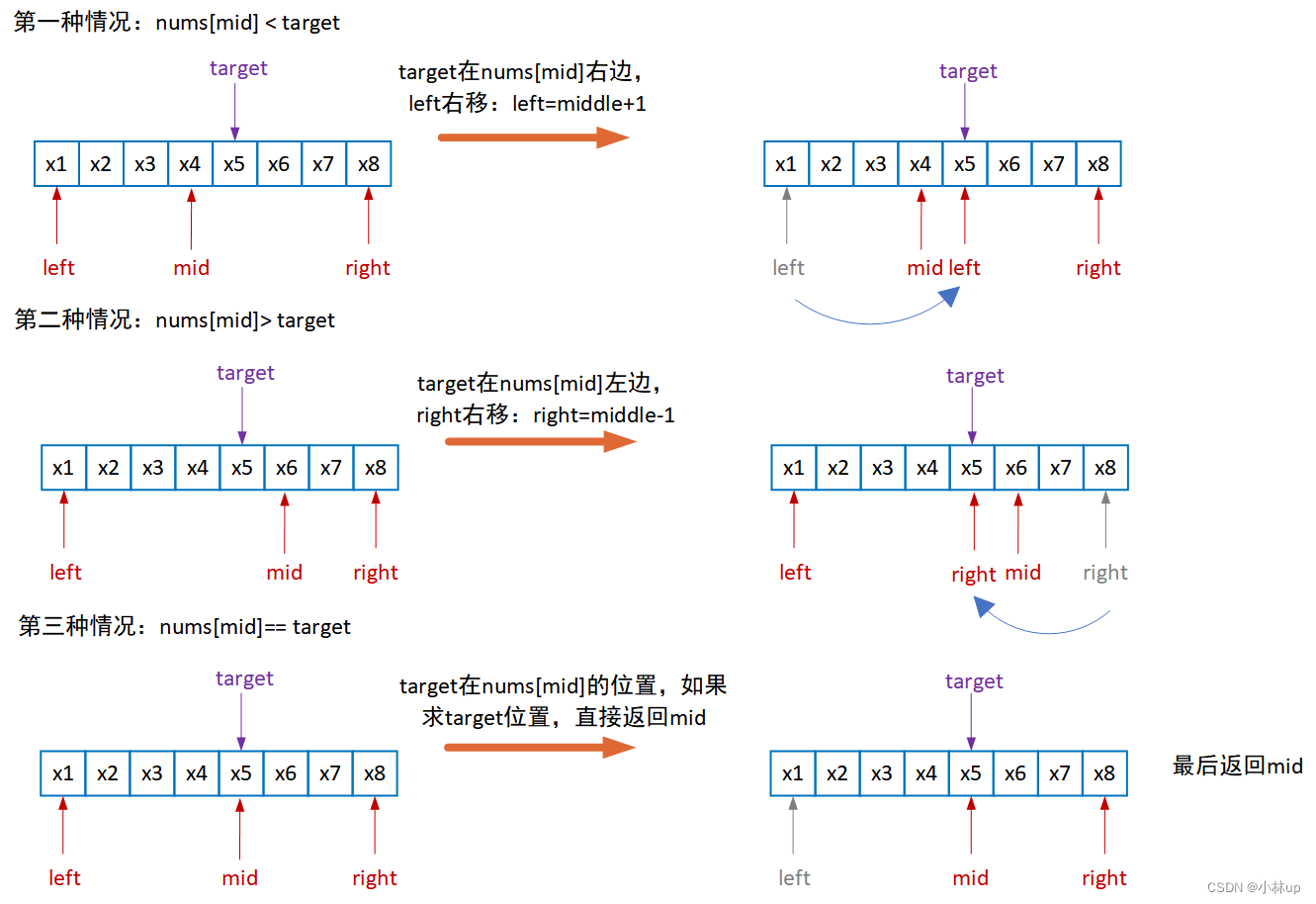
这是标准二分法，对应力扣的704. 二分查找：

求值为target的索引

int search(vector<int>& nums, int target) {int left = 0; int right = nums.size();while (left < right){int mid = left + (right - left) / 2;if (nums[mid] > target)right = mid;else if (nums[mid] < target)left = mid + 1;elsereturn mid;}return -1;
}

在这里插入图片描述

求左右边界

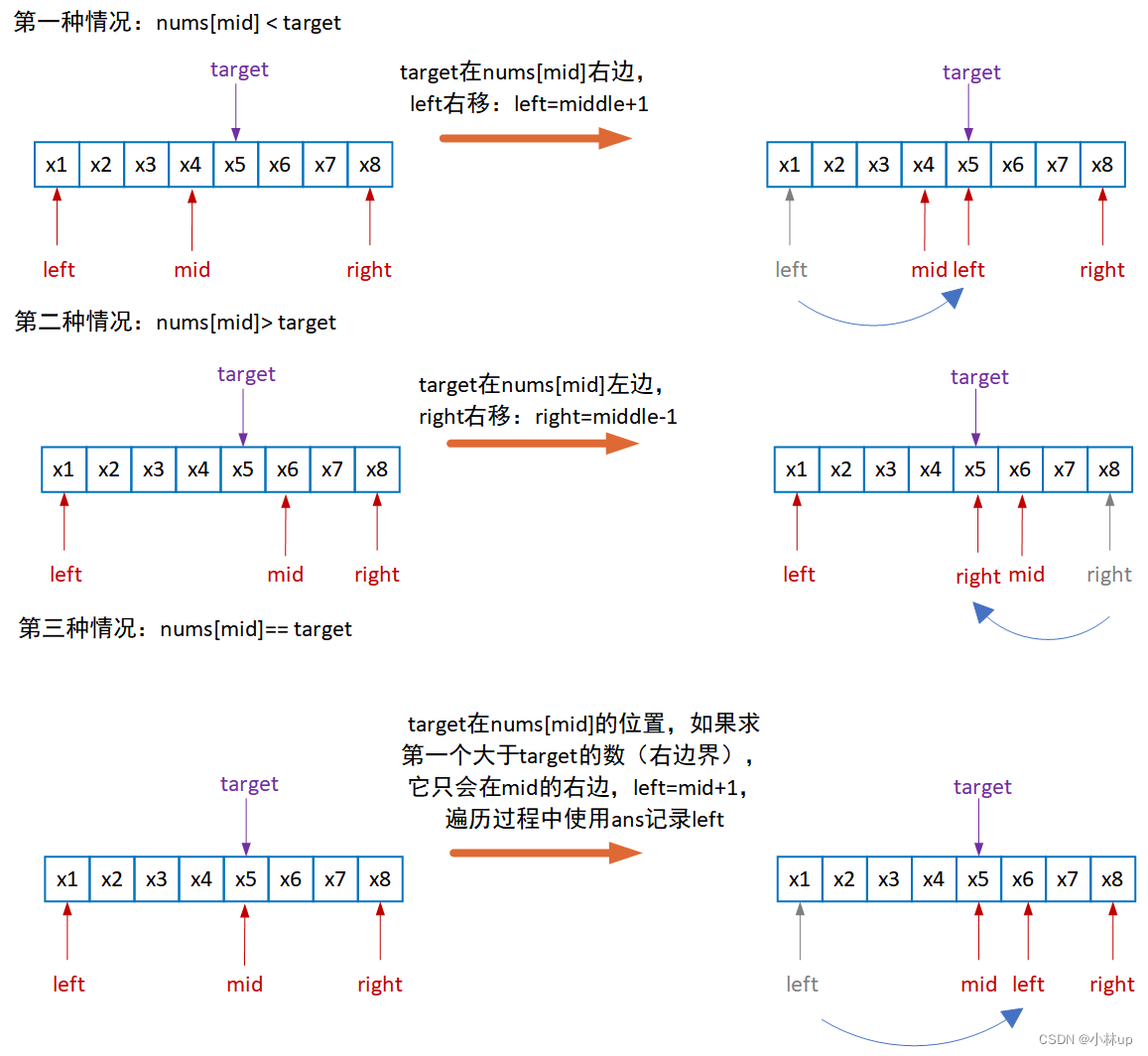
二分法还可以求第一个大于target的索引和第一个小于target的索引

求第一个大于target的值的索引（右边界）

int getRightIndex(vector<int>& nums, int target)
{int left = 0; int right = nums.size() - 1;int rightBorder = -2;while (left <= right){int mid = left + (right - left) / 2;if (nums[mid] > target)right = mid - 1;else{left = mid + 1;rightBorder = left;}}return rightBorder;
}

在这里插入图片描述

力扣的35. 搜索插入位置也可以用这个思路解决：

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0; int right = nums.size() - 1;int rightBorder = 0;while (left <= right){int mid = left + (right - left) / 2;if (nums[mid] > target)right = mid - 1;else{left = mid + 1;rightBorder = left;}}if (rightBorder == 0){return 0;}else{if (nums[rightBorder - 1] != target)return rightBorder;elsereturn rightBorder - 1;}}
};

当然只有一个target也有更简洁的写法，左闭右闭的写法里最后的left就是右边界了：

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;while (left <= right){int mid = left + (right - left) / 2;if (nums[mid] > target)right = mid - 1;else if (nums[mid] < target)left = mid + 1;elsereturn mid;}return left;}
};

求第一个小于target的值的索引（左边界）

int getLeftIndex(vector<int>& nums, int target)
{int left = 0; int right = nums.size() - 1;int leftBorder = -2;while (left <= right){int mid = left + (right - left) / 2;if (nums[mid] < target)left = mid + 1;else{right = mid - 1;leftBorder = right;}}return leftBorder;
}

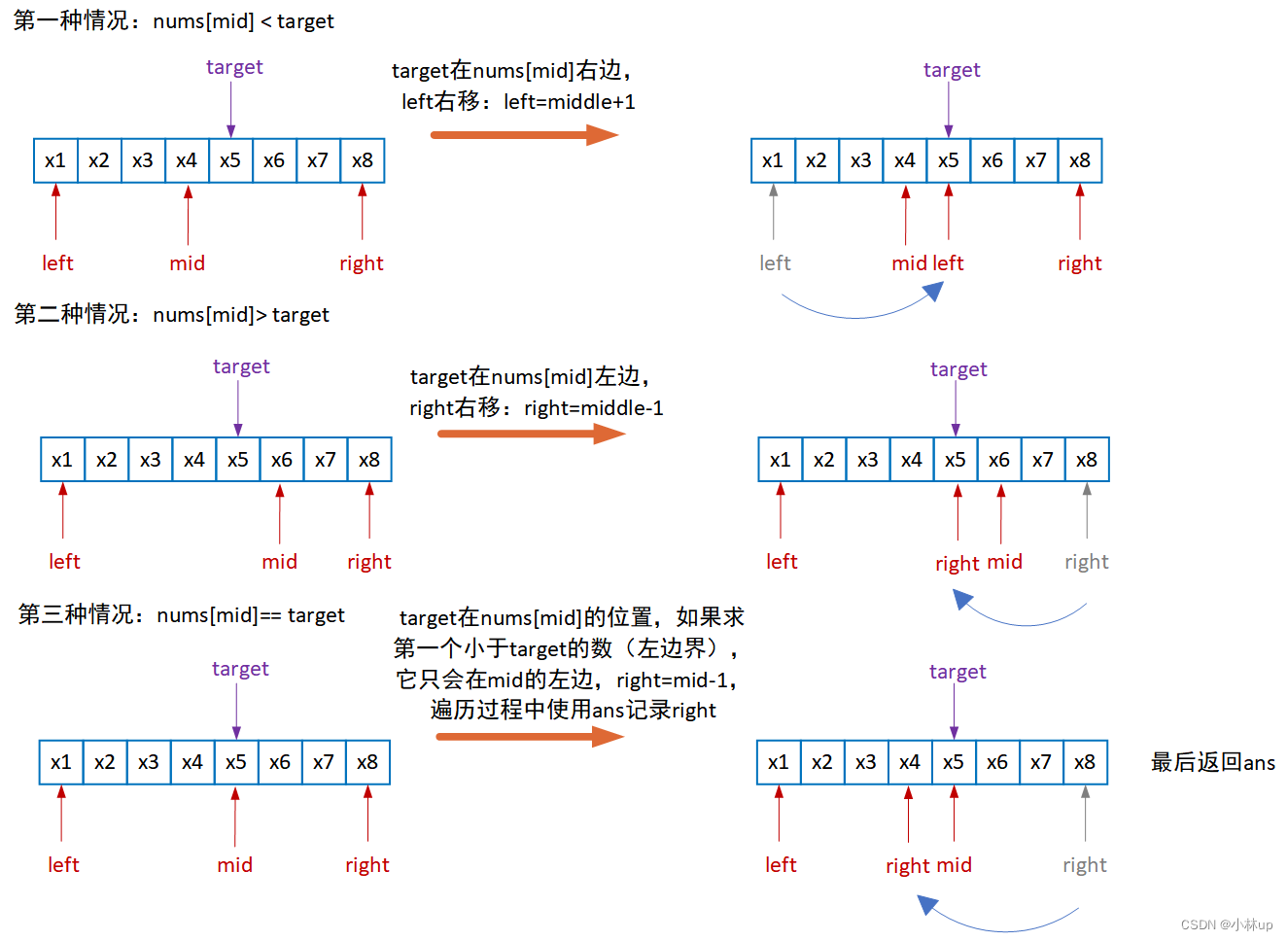
在这里插入图片描述

使用上面两种方法求第一个大于target的索引和第一个小于target的索引对应的是力扣的34. 在排序数组中查找元素的第一个和最后一个位置。第一个target出现的索引和最后一个target出现的索引，对应的就是左边界+1和右边界-1，题目的完整代码：

class Solution {
public:int getRightIndex(vector<int>& nums, int target){int left = 0; int right = nums.size() - 1;int rightBorder = -2;while (left <= right){int mid = left + (right - left) / 2;if (nums[mid] > target)right = mid - 1;else{left = mid + 1;rightBorder = left;}}return rightBorder;}int getLeftIndex(vector<int>& nums, int target){int left = 0; int right = nums.size() - 1;int leftBorder = -2;while (left <= right){int mid = left + (right - left) / 2;if (nums[mid] < target)left = mid + 1;else{right = mid - 1;leftBorder = right;}}return leftBorder;}vector<int> searchRange(vector<int>& nums, int target) {int leftBorder = getLeftIndex(nums, target);int rightBorder = getRightIndex(nums, target);if (leftBorder == -2 || rightBorder == -2)return {-1, -1};if (rightBorder - leftBorder > 1)return {leftBorder + 1, rightBorder - 1};return {-1, -1};}
};