Python - 深夜数据结构与算法之 Graph

一.引言

二.图的简介

1.Graph 图

2.Undirected graph 无向图

3.Directed Graph 有向图

4.DFS / BFS 遍历

三.经典算法实战

1.Num-Islands [200]

2.Land-Perimeter [463]

3.Largest-Island [827]

四.总结

一.引言

Graph 无论是应用还是算法题目在日常生活中比较少见，但是其应用非常广泛，现在社交关系网络很多内容都是基于 Graph 构建的，例如我们常见的各类 GraphEmbedding，其就是基于社交关系网络图进行游走生成对应 Node Embedding。

二.图的简介

1.Graph 图

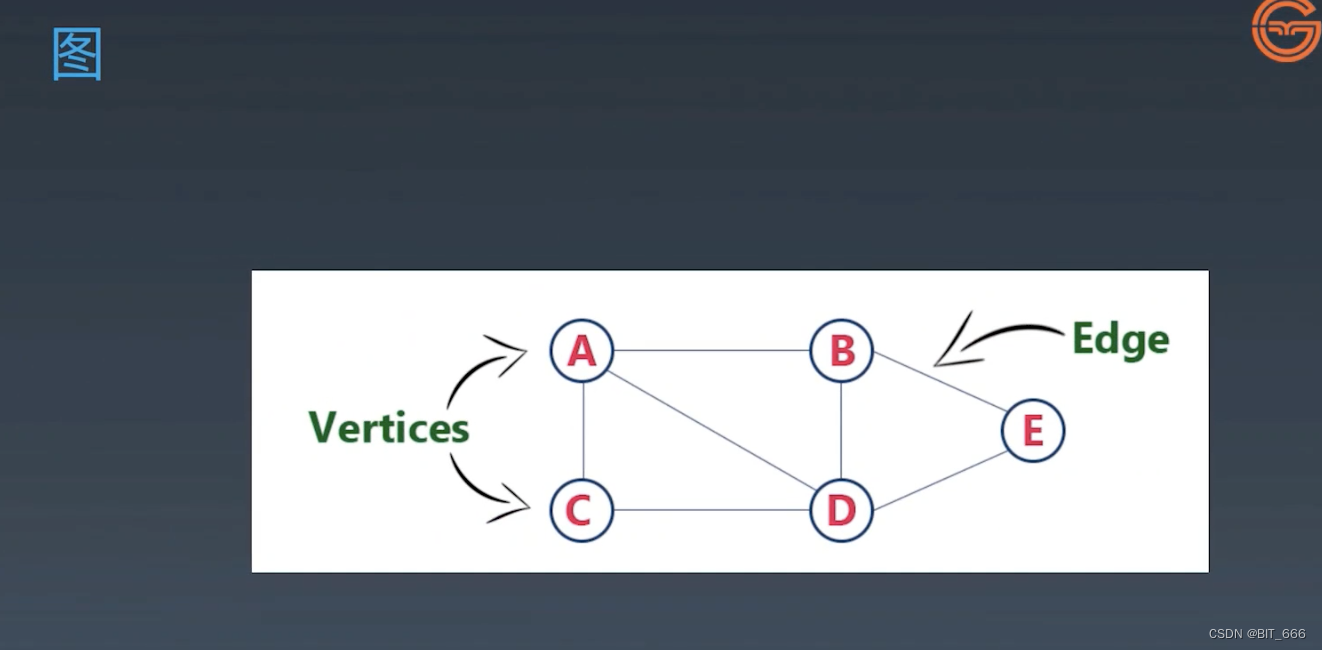
由点和边构成的数据结构即可称之为图，其在代码中一班以 Graph(V, E) 来表示，其中 V 代表点，是顶点的有穷非空集合，E 代表边，是 V 中顶点偶对的有穷集合，偶对我们可以理解为每一条边都有左右两个端点，所以需要偶对。点有入度和出度之分，即从该点出发有几条路径，如果是无向图二者相等。边除了方向外，有的场景还有权重，例如社交场景评估两个相邻用户的亲密度 E 就是有权重的，默认情况下所有边的权重均为 1，即众生平等。

2.Undirected graph 无向图

◆ 无向无权图

图一般使用邻接矩阵或邻接列表的形式表示点之间的关系，边的关系则蕴含在两点之间。

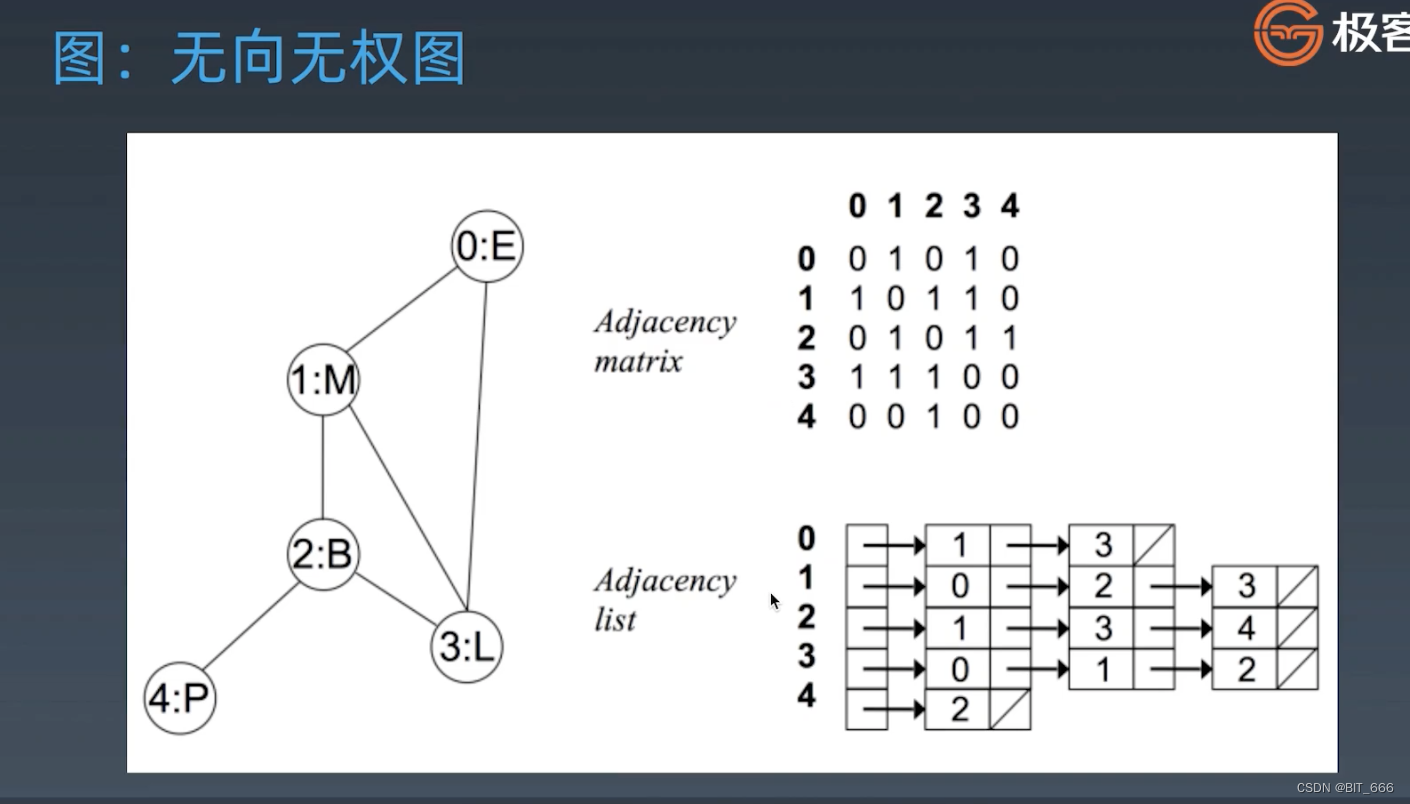
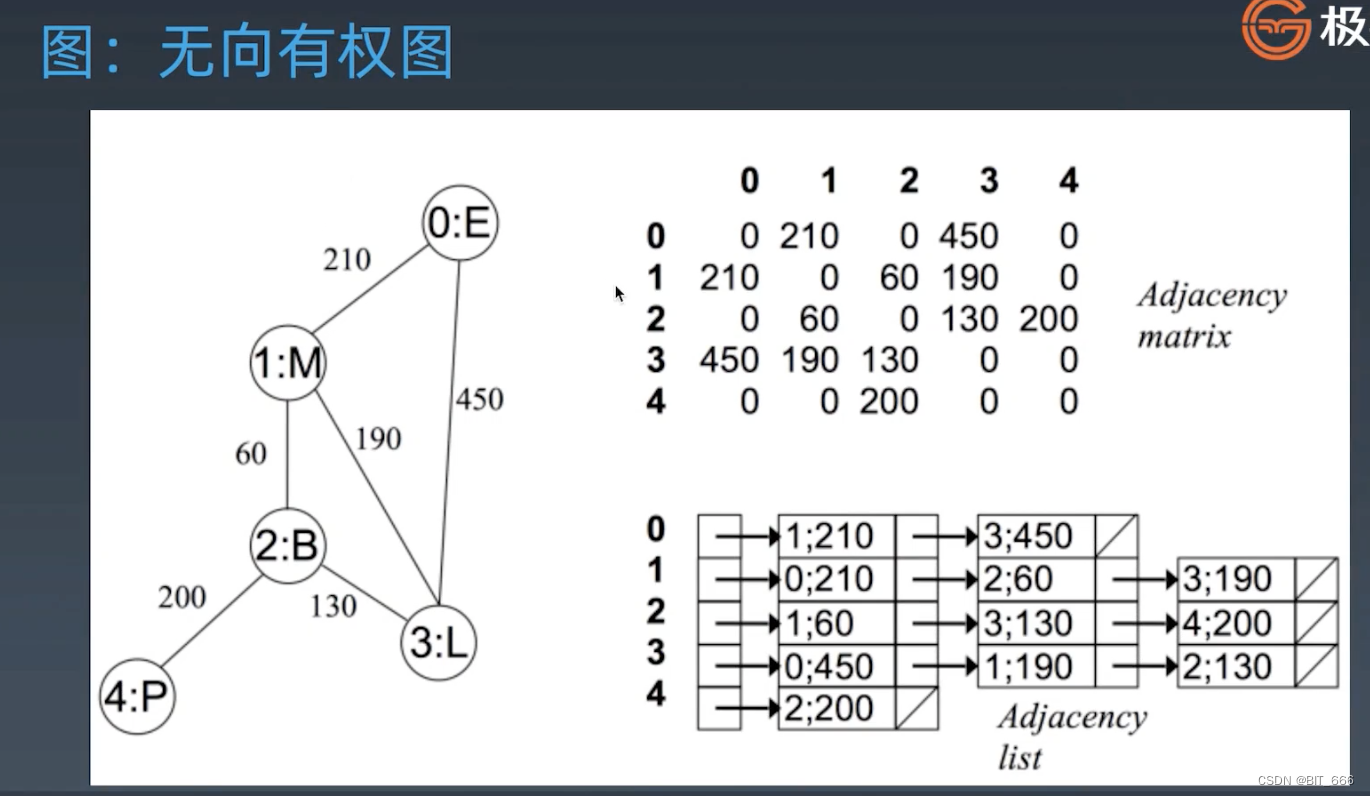
◆ 无向有权图

默认情况下，边的权重都唯一，实际工业场景下，边之间往往通过 weight 来描述两个点之间的关联程度，如果使用邻接矩阵，那么直接在对应位置赋值 weight 即可，如果是邻接列表则可以使用一个二元组进行表示。注意: 不论是无向有权还是无向无权，其对应的邻接矩阵是对称矩阵，因为 0-1 相连必然 1-0 也相连。

3.Directed Graph 有向图

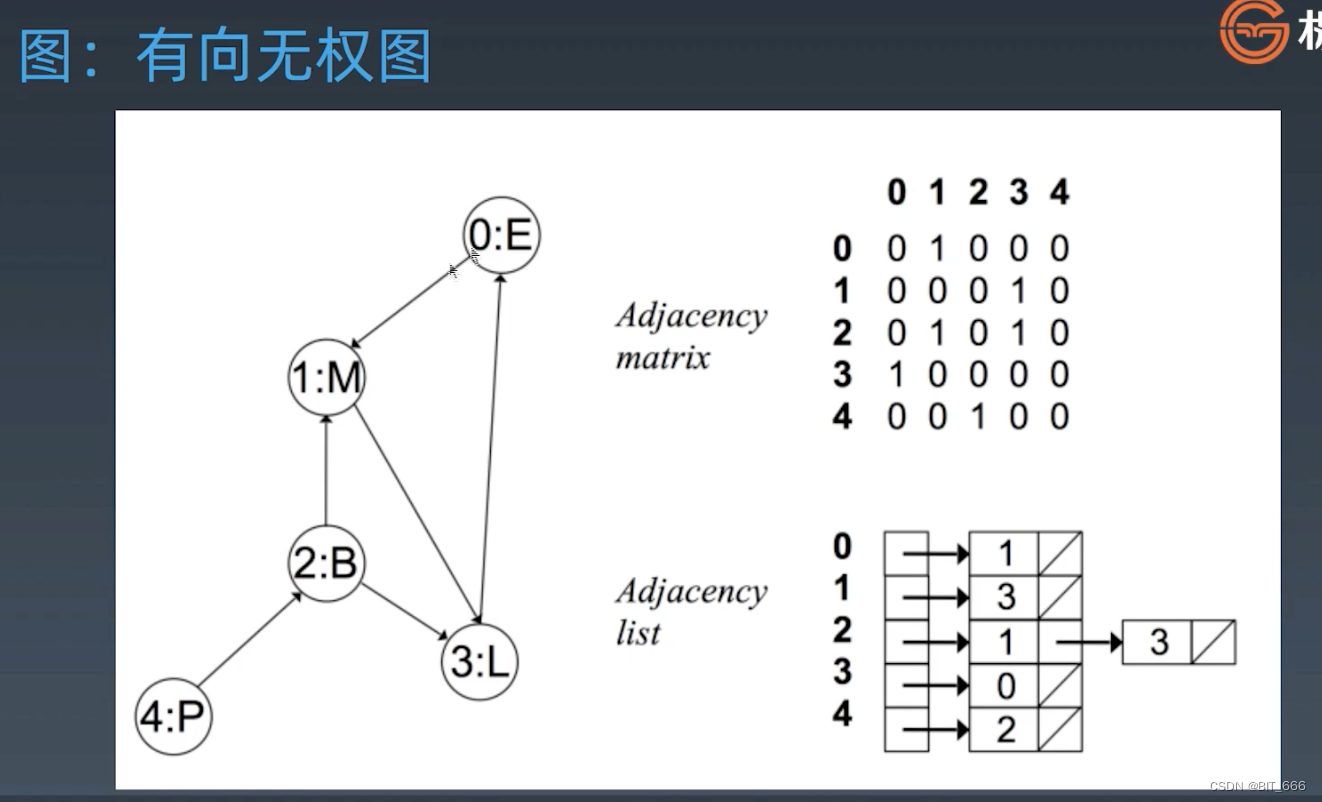
有向图只会在存在的方向上表示，例如 0->1，那么邻接矩阵 [0, 1] 是有值的，但 [1, 0] 为 0，此时邻接矩阵就不在是对称矩阵，除非每个边都是双向的。有向有权图可以参考上面的无向有权图，我们只需给矩阵修改 weights，数组转换为二元组即可。

4.DFS / BFS 遍历

◆ DFS

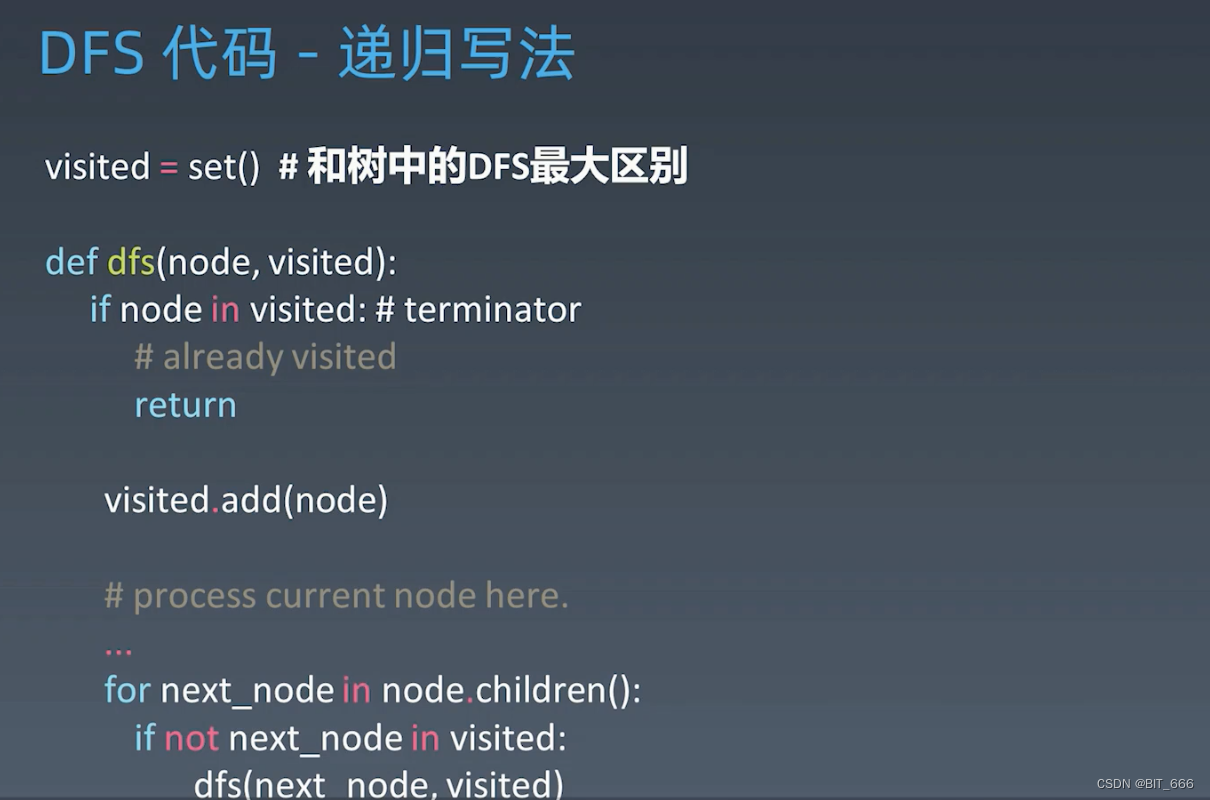
深度优先遍历，这里与二叉树的遍历有一点不同是图可能存在环，从而导致元素重复，所以需要进行节点的去重。其实现遵循递归，也满足递归的三要素：

- 边界条件判断节点是否被访问

- 处理逻辑添加当前处理的点

- 自身调用继续处理未处理的点

处理中不断向 next_node 出发，所以是深度优先。

◆ BFS

广度优先遍历，其会向两边扩展搜索，二叉树的层数遍历就可以通过 BFS 实现，下面方法中 generate_related_nodes 其实就是搜索两边或者周围节点的伪代码，后续我们会带来 DFS、BFS 更详细的介绍和代码。大家在这里只要明确图遍历中，DFS 和 BFS 是很重要的两种方法即可。

三.经典算法实战

1.Num-Islands [200]

岛屿数量: https://leetcode.cn/problems/number-of-islands/

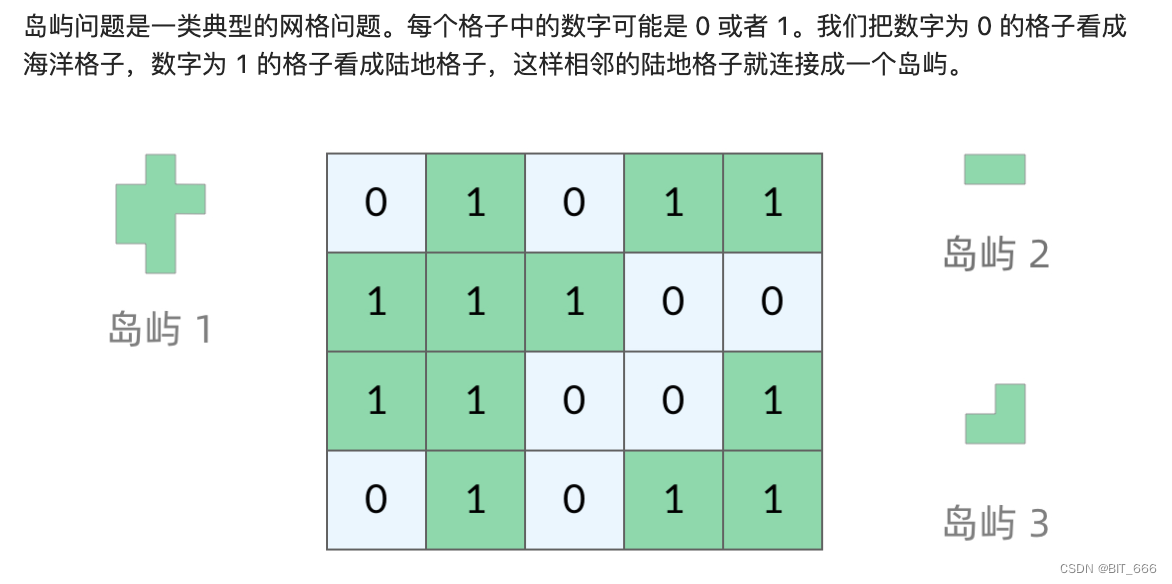
◆ 题目分析

海岛的形态与数字 0、1 的关系，我们需要遍历一个点周围的情况判断，以 [0, 1] 的点为例，我们以其为起点进行遍历，对于二叉树而言，其拥有 left 和 right 两个遍历方向，而对于网格问题，其拥有上下左右四个方向，遇到 1 就继续遍历，遇到 0 则停止遍历，当无法继续扩展时，代表遍历完成，此时就生成一个岛屿。这里还有一个问题，就是 for 循环遍历岛中的节点，会有重复的情况，例如遍历 [0, 1] 和 [1, 1] 的点都可以生成岛屿 1，所以这里我们还要对遍历过的岛屿进行标记，防止其他节点再扩展，这样重复的问题也可以解决。

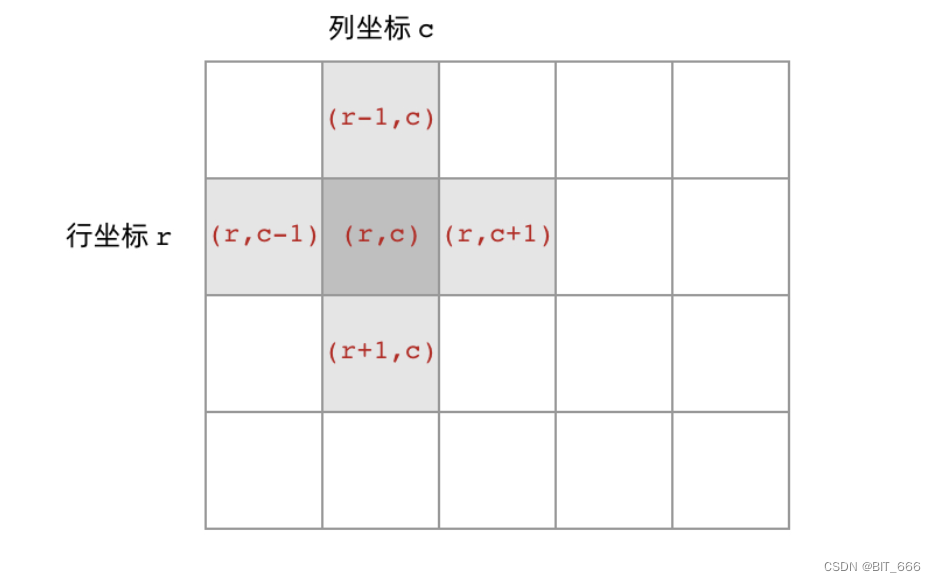
至于上下左右的界定，我们针对 (x, y) ± 1 即可，需要注意出格的行为，即 (x, y) 超出岛屿范围。和二叉树类比的话，停止条件就是遇到 0 或者遇到访问过的点 Visted Point 或者出格 Out of Bound，就好比是 root == None；而遍历 left、rigth 则变成 (r-1, c)、.....、(r+1, c)。

◆ DFS

class Solution(object):def numIslands(self, grid):""":type grid: List[List[str]]:rtype: int"""# 异常情况if not grid:return 0# 记录岛屿数量count = 0# 遍历岛屿for row in range(len(grid)):for col in range(len(grid[0])):if grid[row][col] == "1":# 沿 (row, col) 递归遍历上下左右self.dfs(grid, row, col)count += 1return countdef inArea(self, grid, row, col):return 0 <= row < len(grid) and 0 <= col < len(grid[0])def dfs(self, grid, row, col):# 不在网格 -> 返回if not self.inArea(grid, row, col):return# 不是岛屿->返回        if grid[row][col] != "1":return# 已遍历标记grid[row][col] = "2"self.dfs(grid, row - 1, col) # 上self.dfs(grid, row + 1, col) # 下self.dfs(grid, row, col - 1) # 左self.dfs(grid, row, col + 1) # 右

inArea 函数负责判断当前点是否在 grid 网格区域内，超出网格则停止 DFS，其次针对遍历过的 "1" 即陆地，为了防止 DFS 重复循环，我们需要将其换一个标记从而避免重复，最后上下左右探索即可。每探索一次，如果能够发现陆地则陆地全部被标记为已走，则下次无法遍历，从而划分出一块一块土地。

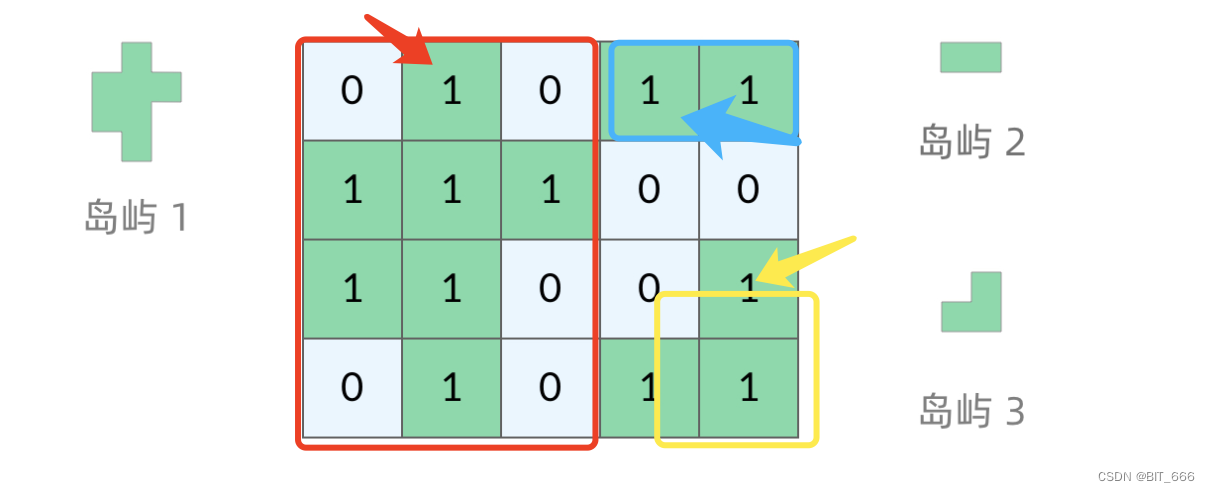
如上图所示，遍历到 [0, 1] 位置时会扩展出岛屿1，遍历到 [0, 3] 位置时扩展出岛屿 2，以此类推，每次 count += 1 即可，当 grid 里没有 "1" 即陆地时，遍历结束。

2.Land-Perimeter [463]

岛屿的周长: https://leetcode.cn/problems/island-perimeter/description/

◆ 题目分析

和上题很像，也是 grid 中的岛屿，这不过这里有一个限定即只有一个岛屿，所以我们 BFS 一次就能 get 到整个岛屿。观察图像可以发现，对于 (row, col) 而言如果下一个点在海里或者 grid 外，这里便存在一个边即属于周长的边，画个图理解下，红色箭头是出 grid 的边，蓝色箭头是入海流，正所谓红头依山尽，蓝头入海流：

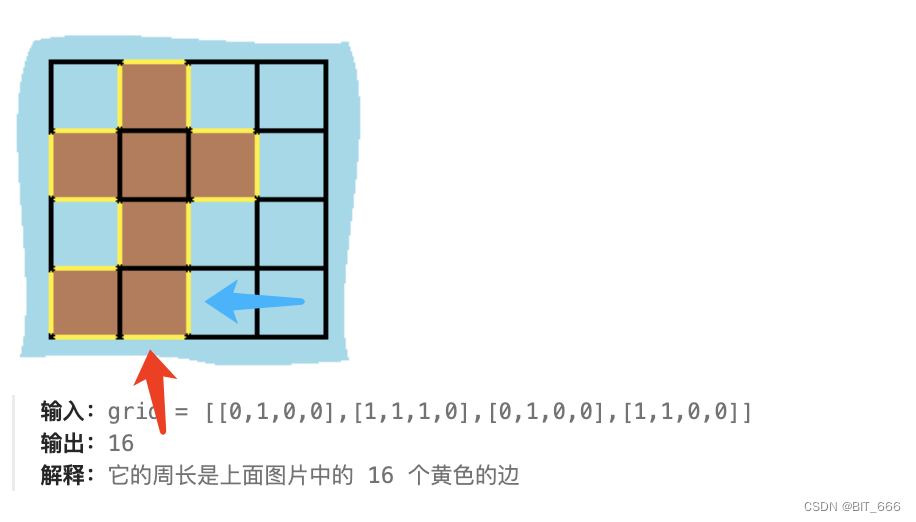
◆ DFS

class Solution(object):def islandPerimeter(self, grid):""":type grid: List[List[int]]:rtype: int"""# 寻找小岛的起点for row in range(len(grid)):for col in range(len(grid[0])):if grid[row][col] == 1:return self.dfs(grid, row, col)return 0# 是否在 grid 网格内def inArea(self, grid, row, col):return 0 <= row < len(grid) and 0 <= col < len(grid[0])def dfs(self, grid, row, col):# 蓝色箭头 -> 出格 -> 边长 + 1if not self.inArea(grid, row, col):return 1# 红色箭头 -> 出海 -> 边长 + 1if grid[row][col] == 0:return 1# 只剩 == "2" 的已经遍历的情况了，忽略if grid[row][col] != 1:return 0grid[row][col] = 2return self.dfs(grid, row - 1, col) + self.dfs(grid, row + 1, col) + self.dfs(grid, row, col - 1) + self.dfs(grid, row, col + 1)

红箭头出海，蓝箭头出格，这两个情况 +1 其余情况说拜拜即可，dfs 遍历思路与上面相同，也是上下左右出发。

3.Largest-Island [827]

造海填路问题: https://leetcode.cn/problems/making-a-large-island/

◆ 题目分析

grid 网格内有多个岛屿，通过将一块海洋改变陆地，求填海造地后最大的面积，这里我们可以借助第一题的思路，先把陆地都照出来，然后遍历 "0" 即海洋，看哪个海洋变成陆地后，可以连接更多土地。除此之外，我们还需要对相连的陆地给与记号，保证面积不会重复累加。

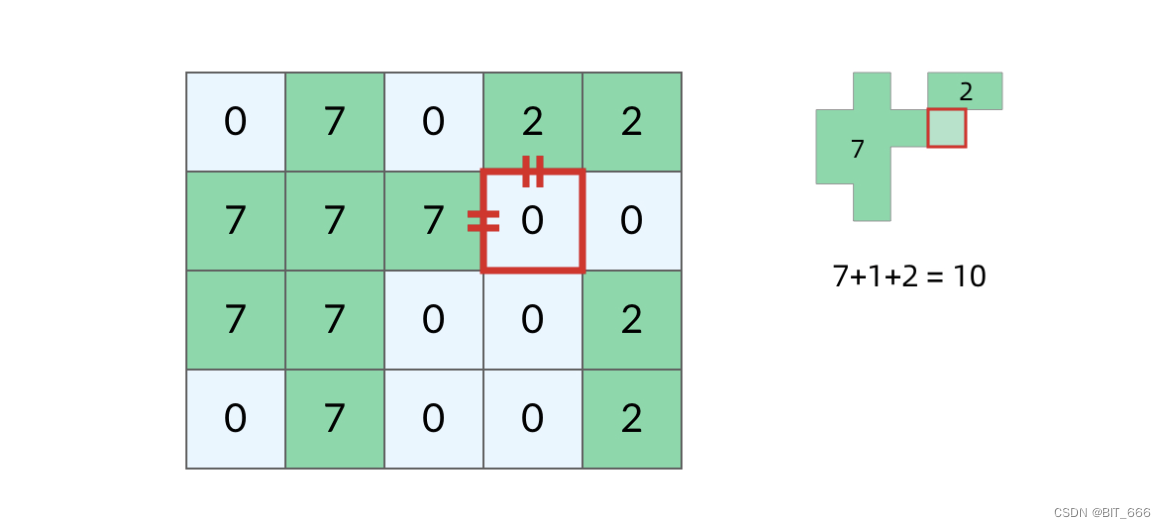
◆ DFS

#!/usr/bin/python
# -*- coding: UTF-8 -*-class Solution(object):def largestIsland(self, grid):""":type grid: List[List[int]]:rtype: int"""if not grid:return 0# 标记访问节点，记录每个岛屿面积index = 2location = {}visited = set()for row in range(len(grid)):for col in range(len(grid[0])):# 每块陆地标记为一个记号if grid[row][col] == 1:self.dfs(grid, row, col, index, location, visited)index += 1# 通过原始岛屿信息更新 maxif location:max_island = max(location.values())else:max_island = 0for row in range(len(grid)):for col in range(len(grid[0])):# 找到海洋并计算联通面积if grid[row][col] == 0:max_island = max(self.getAroundArea(grid, row, col, location), max_island)return max_islanddef getAroundArea(self, grid, row, col, location):# 记录最大面积res = 1# 同一块陆地算一次area = set()# 上下左右找陆地if self.inArea(grid, row + 1, col) and grid[row + 1][col] != 0:area.add(grid[row + 1][col])if self.inArea(grid, row - 1, col) and grid[row - 1][col] != 0:area.add(grid[row - 1][col])if self.inArea(grid, row, col + 1) and grid[row][col + 1] != 0:area.add(grid[row][col + 1])if self.inArea(grid, row, col - 1) and grid[row][col - 1] != 0:area.add(grid[row][col - 1])# 土地去重相加if location and area:for index in area:res += location[index]return resdef dfs(self, grid, row, col, index, location, visted):# 不在网格 -> 返回if not self.inArea(grid, row, col):return# 不是岛屿->返回if grid[row][col] != 1:return# 已遍历标记grid[row][col] = indexif index not in location:location[index] = 0if (row, col) not in visted:visted.add((row, col))location[index] += 1self.dfs(grid, row - 1, col, index, location, visted)  # 上self.dfs(grid, row + 1, col, index, location, visted)  # 下self.dfs(grid, row, col - 1, index, location, visted)  # 左self.dfs(grid, row, col + 1, index, location, visted)  # 右# 是否在 grid 网格内def inArea(self, grid, row, col):return 0 <= row < len(grid) and 0 <= col < len(grid[0])

dfs 负责在 grid 中寻找土地并标记，getAroundArea 负责遍历每一片海，并在海的上下左右寻找可能存在的岛屿，如果存在则将此地造海 res = 1，再加上发现的陆地的面积，最后更新 max 即可。这个方法的优点是思路很好理解，但是本题边界情况很多，需要判断的空 set、dict 也很多，而且遍历多次时间复杂度也较高。