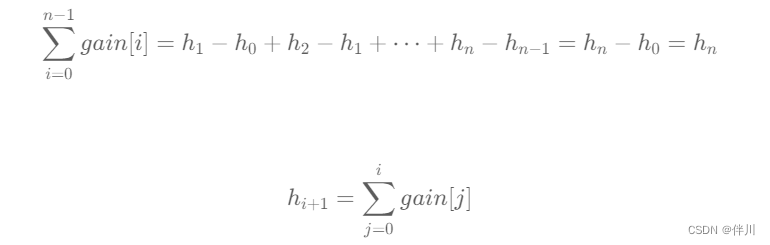目录
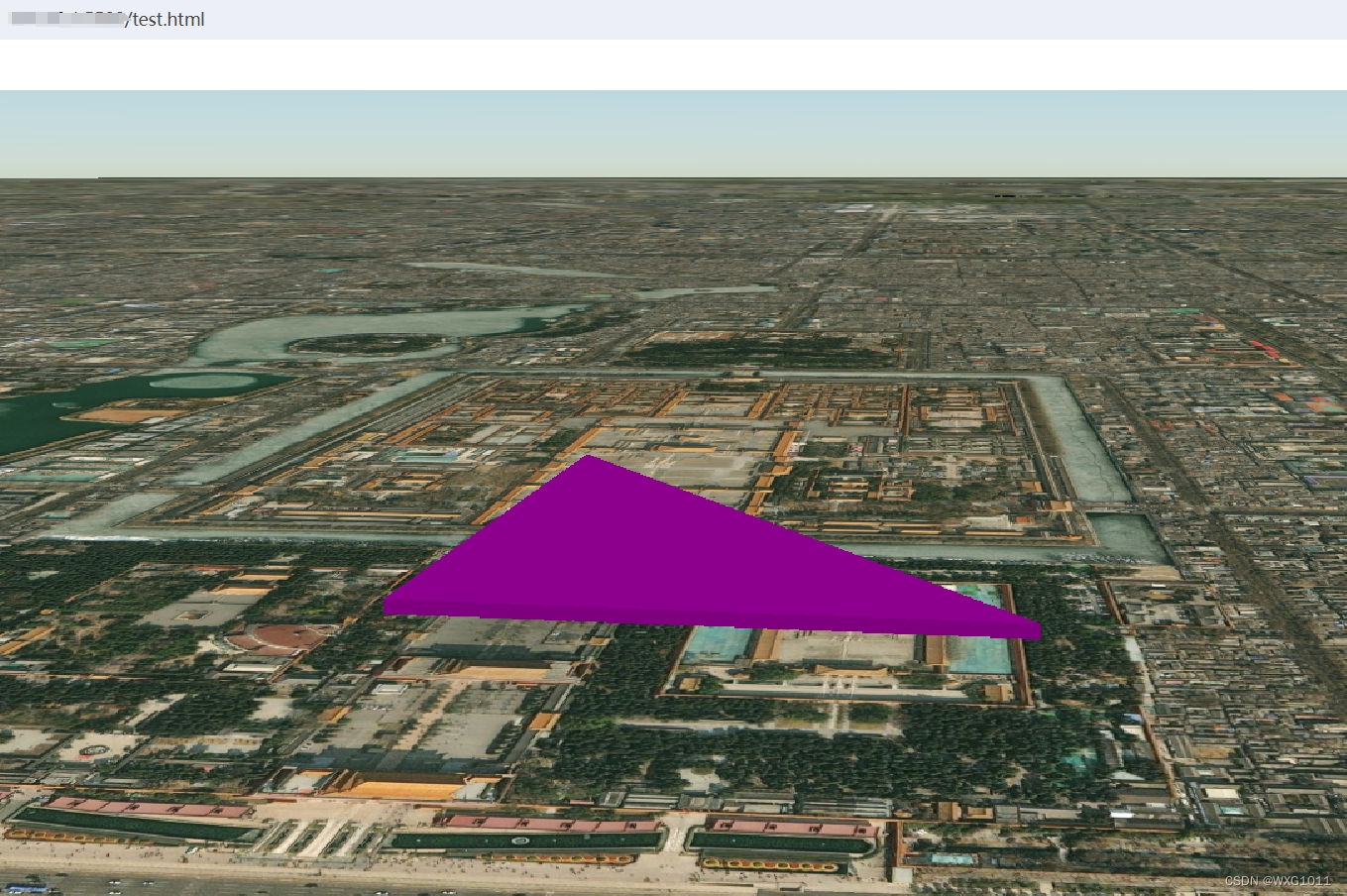
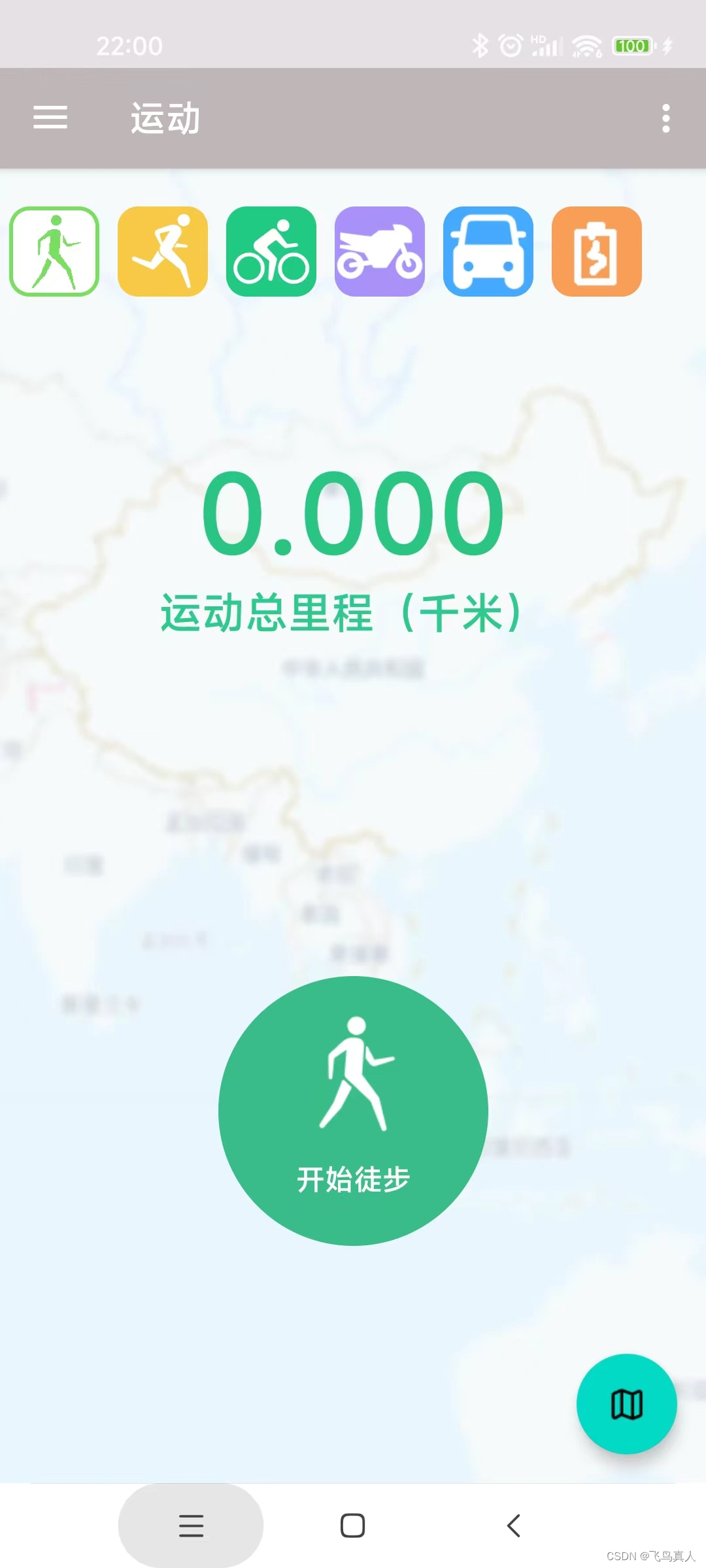
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
4.1 包围盒构建
4.2 点云压缩
4.3 曲面重建
5.算法完整程序工程
1.算法运行效果图预览

2.算法运行软件版本
matlab2022a
3.部分核心程序
............................................................................
%包围盒中心坐标
XYZc = zeros(X_w*Y_w*Z_h,3);
for i=1:X_wXc = Xmin+LL*(i-0.5);for j=1:Y_wYc = Ymin+LL*(j-0.5);for k=1:Z_hZc = Zmin+LL*(k-0.5);XYZc((i-1)*Y_w*Z_h+(j-1)*Z_h+k,1)=Xc;XYZc((i-1)*Y_w*Z_h+(j-1)*Z_h+k,2)=Yc;XYZc((i-1)*Y_w*Z_h+(j-1)*Z_h+k,3)=Zc;endend
end
%中心点与各个点云之间的距离矩阵
Mdist=zeros(Rr,4);
for i=1:RrMdist(i,1)=X_w2(i);Mdist(i,2)=Y_w2(i);Mdist(i,3)=Z_h2(i);Mdist(i,4)=sqrt((XYZc((X_w2(i)-1)*Y_w*Z_h+(Y_w2(i)-1)*Z_h+Z_h2(i),1)-Data_3d(i,1))^2+...(XYZc((X_w2(i)-1)*Y_w*Z_h+(Y_w2(i)-1)*Z_h+Z_h2(i),2)-Data_3d(i,2))^2+...(XYZc((X_w2(i)-1)*Y_w*Z_h+(Y_w2(i)-1)*Z_h+Z_h2(i),3)-Data_3d(i,3))^2);
end
[Y,X_w,Y_w]=unique(Mdist(:,1:3),'rows');X =zeros(length(X_w),1);
for i=1:length(X_w)X(i)=max(Mdist(Y_w==i,4));
end
Y=[Y X];Data_box = Y(:,1:3);
[t] = MyCrust(Data_box);
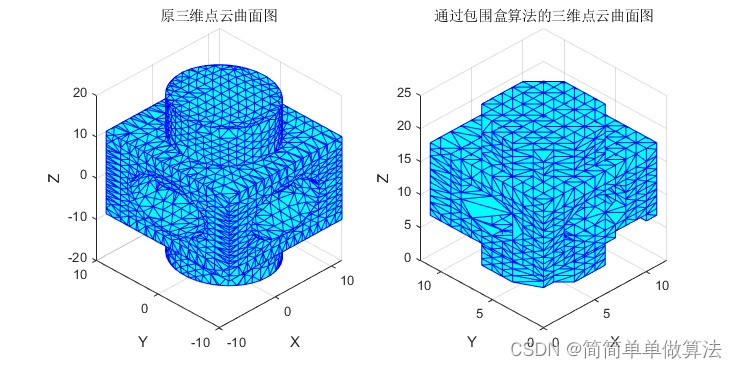
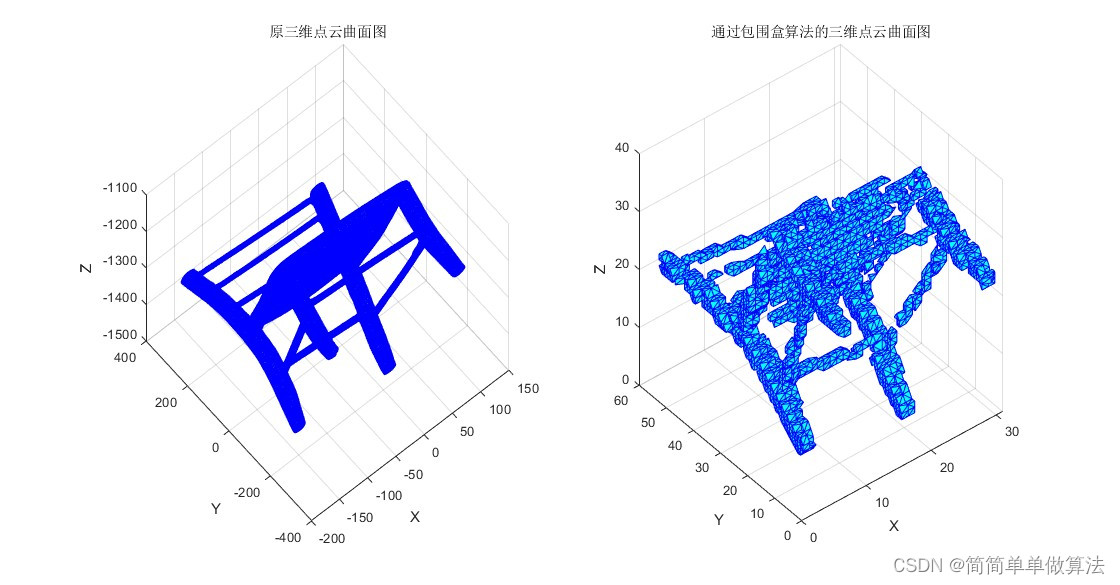
[w] = MyCrust(Data_3d);%原三维点云曲面图
figure
subplot(121);
axis equal
trisurf(w,Data_3d(:,1),Data_3d(:,2),Data_3d(:,3),'facecolor','c','edgecolor','b')
grid on
view(-45,30)
xlabel('X');
ylabel('Y');
zlabel('Z');
title('原三维点云曲面图');%通过包围盒算法的三维点云曲面图
subplot(122);
axis equal
trisurf(t,Data_box(:,1),Data_box(:,2),Data_box(:,3),'facecolor','c','edgecolor','b')
grid on
view(-45,30)
xlabel('X');
ylabel('Y');
zlabel('Z');
title('通过包围盒算法的三维点云曲面图');
954.算法理论概述
随着三维扫描技术的快速发展,三维点云数据在多个领域,如计算机视觉、机器人技术和逆向工程中得到了广泛应用。然而,大规模的点云数据不仅存储成本高,而且处理速度慢,这限制了其在实时应用中的使用。为了解决这个问题,本文提出了一种基于包围盒算法的三维点云数据压缩和曲面重建方法。该方法通过减少点的数量同时保留原始点云的主要特征,从而实现了高效的数据压缩和精确的曲面重建。
三维点云是空间中一系列点的集合,每个点都有其特定的坐标(x, y, z)。这些点可以通过各种方式获得,例如激光扫描、立体视觉等。随着技术的进步,获取的点云数据越来越密集,导致数据量迅速增长。因此,如何有效地压缩这些数据并从中重建出曲面成为了一个重要的问题。在过去的几十年中,许多研究致力于点云数据的压缩和曲面重建。其中,一些方法基于体素网格进行空间划分,另一些则使用迭代的方法对点进行聚类。然而,这些方法在处理大规模、高密度的点云数据时往往效率低下。
基于包围盒算法的压缩与重建分为三个步骤:包围盒构建、点云压缩和曲面重建。
4.1 包围盒构建
首先,我们为整个点云构建一个初始的包围盒。然后,递归地将这个包围盒划分为更小的子盒,直到满足某个停止条件(如子盒中的点数少于某个阈值)。每个子盒都包含了一部分点云数据。
4.2 点云压缩
在每个子盒中,我们选择一个代表点来代替该盒子中的所有点。代表点的选择可以基于多种策略,如盒子的中心点或点云的质心。通过这种方式,大量的点被少数几个代表点所替代,从而实现了数据的压缩。
数学上,假设一个子盒B包含n个点{p1, p2, ..., pn},每个点的坐标为(x, y, z)。该子盒的代表点Pr可以计算为:
(Pr = \frac{1}{n} \sum_{i=1}^{n} p_i)
这里,Pr是子盒中所有点的坐标平均值。
4.3 曲面重建
在得到压缩后的代表点后,我们使用这些点作为控制点来构建一个三角网格,从而近似原始点云的曲面。具体地,我们可以使用Delaunay三角剖分或Ball Pivoting算法来生成三角网格。
5.算法完整程序工程
OOOOO
OOO
O